Distributionally Robust Reduced Rank Regression and Principal Component Analysis in High Dimensions

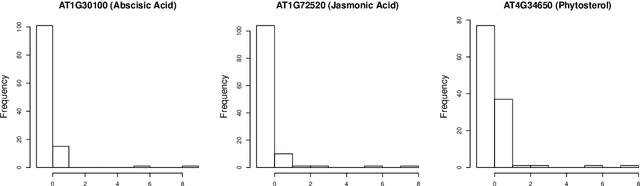
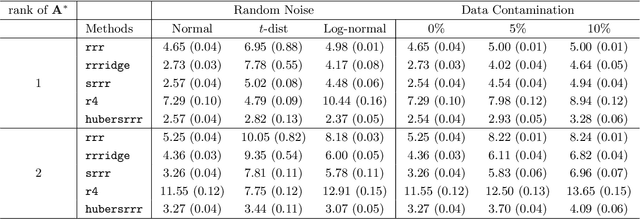
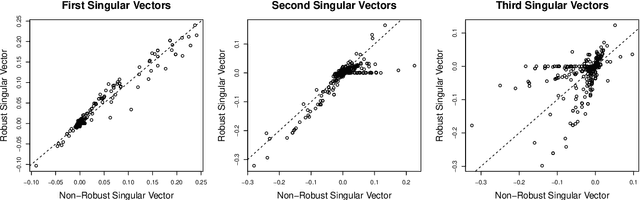
We propose robust sparse reduced rank regression and robust sparse principal component analysis for analyzing large and complex high-dimensional data with heavy-tailed random noise. The proposed methods are based on convex relaxations of rank-and sparsity-constrained non-convex optimization problems, which are solved using the alternating direction method of multipliers (ADMM) algorithm. For robust sparse reduced rank regression, we establish non-asymptotic estimation error bounds under both Frobenius and nuclear norms, while existing results focus mostly on rank-selection and prediction consistency. Our theoretical results quantify the tradeoff between heavy-tailedness of the random noise and statistical bias. For random noise with bounded $(1+\delta)$th moment with $\delta \in (0,1)$, the rate of convergence is a function of $\delta$, and is slower than the sub-Gaussian-type deviation bounds; for random noise with bounded second moment, we recover the results obtained under sub-Gaussian noise. Furthermore, the transition between the two regimes is smooth. For robust sparse principal component analysis, we propose to truncate the observed data, and show that this truncation will lead to consistent estimation of the eigenvectors. We then establish theoretical results similar to those of robust sparse reduced rank regression. We illustrate the performance of these methods via extensive numerical studies and two real data applications.