Graphical Nonconvex Optimization for Optimal Estimation in Gaussian Graphical Models
Paper and Code
Jun 04, 2017

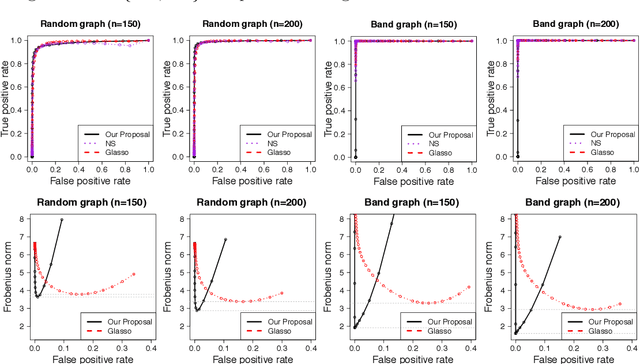
We consider the problem of learning high-dimensional Gaussian graphical models. The graphical lasso is one of the most popular methods for estimating Gaussian graphical models. However, it does not achieve the oracle rate of convergence. In this paper, we propose the graphical nonconvex optimization for optimal estimation in Gaussian graphical models, which is then approximated by a sequence of convex programs. Our proposal is computationally tractable and produces an estimator that achieves the oracle rate of convergence. The statistical error introduced by the sequential approximation using the convex programs are clearly demonstrated via a contraction property. The rate of convergence can be further improved using the notion of sparsity pattern. The proposed methodology is then extended to semiparametric graphical models. We show through numerical studies that the proposed estimator outperforms other popular methods for estimating Gaussian graphical models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge