Stochastic Gradient Descent without Full Data Shuffle

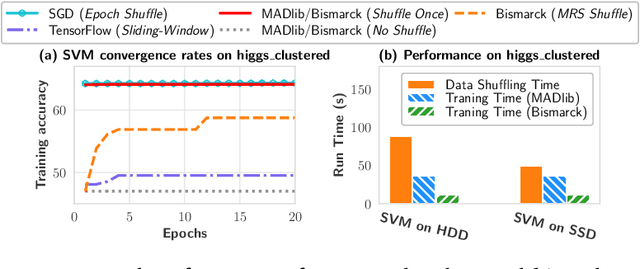
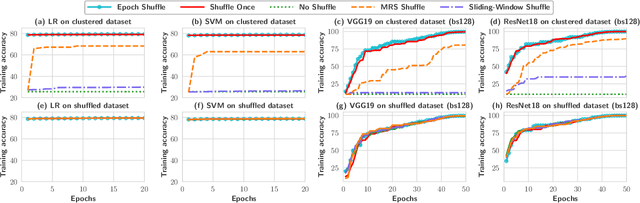
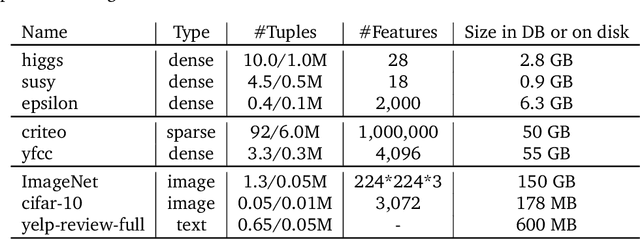
Stochastic gradient descent (SGD) is the cornerstone of modern machine learning (ML) systems. Despite its computational efficiency, SGD requires random data access that is inherently inefficient when implemented in systems that rely on block-addressable secondary storage such as HDD and SSD, e.g., TensorFlow/PyTorch and in-DB ML systems over large files. To address this impedance mismatch, various data shuffling strategies have been proposed to balance the convergence rate of SGD (which favors randomness) and its I/O performance (which favors sequential access). In this paper, we first conduct a systematic empirical study on existing data shuffling strategies, which reveals that all existing strategies have room for improvement -- they all suffer in terms of I/O performance or convergence rate. With this in mind, we propose a simple but novel hierarchical data shuffling strategy, CorgiPile. Compared with existing strategies, CorgiPile avoids a full data shuffle while maintaining comparable convergence rate of SGD as if a full shuffle were performed. We provide a non-trivial theoretical analysis of CorgiPile on its convergence behavior. We further integrate CorgiPile into PyTorch by designing new parallel/distributed shuffle operators inside a new CorgiPileDataSet API. We also integrate CorgiPile into PostgreSQL by introducing three new physical operators with optimizations. Our experimental results show that CorgiPile can achieve comparable convergence rate with the full shuffle based SGD for both deep learning and generalized linear models. For deep learning models on ImageNet dataset, CorgiPile is 1.5X faster than PyTorch with full data shuffle. For in-DB ML with linear models, CorgiPile is 1.6X-12.8X faster than two state-of-the-art in-DB ML systems, Apache MADlib and Bismarck, on both HDD and SSD.

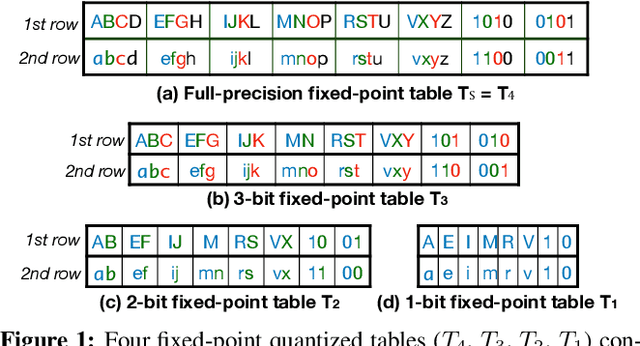
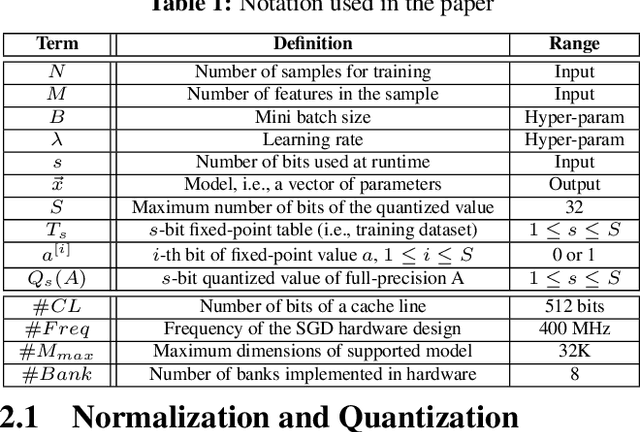
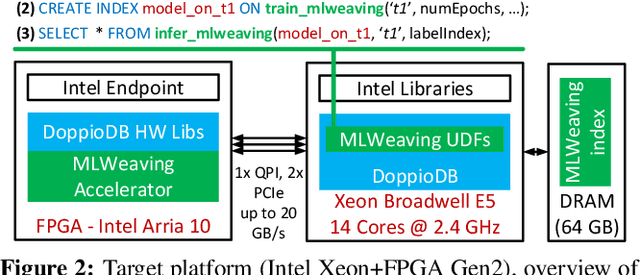
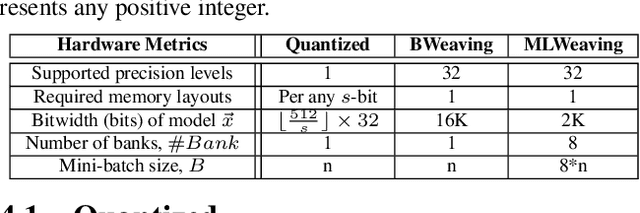
Accelerating Generalized Linear Models with MLWeaving: A One-Size-Fits-All System for Any-precision Learning (Technical Report)

Learning from the data stored in a database is an important function increasingly available in relational engines. Methods using lower precision input data are of special interest given their overall higher efficiency but, in databases, these methods have a hidden cost: the quantization of the real value into a smaller number is an expensive step. To address the issue, in this paper we present MLWeaving, a data structure and hardware acceleration technique intended to speed up learning of generalized linear models in databases. ML-Weaving provides a compact, in-memory representation enabling the retrieval of data at any level of precision. MLWeaving also takes advantage of the increasing availability of FPGA-based accelerators to provide a highly efficient implementation of stochastic gradient descent. The solution adopted in MLWeaving is more efficient than existing designs in terms of space (since it can process any resolution on the same design) and resources (via the use of bit-serial multipliers). MLWeaving also enables the runtime tuning of precision, instead of a fixed precision level during the training. We illustrate this using a simple, dynamic precision schedule. Experimental results show MLWeaving achieves up to16 performance improvement over low-precision CPU implementations of first-order methods.

Compressive Sensing with Low Precision Data Representation: Theory and Applications

Modern scientific instruments produce vast amounts of data, which can overwhelm the processing ability of computer systems. Lossy compression of data is an intriguing solution, but comes with its own dangers, such as potential signal loss, and the need for careful parameter optimization. In this work, we focus on a setting where this problem is especially acute -compressive sensing frameworks for radio astronomy- and ask: Can the precision of the data representation be lowered for all inputs, with both recovery guarantees and practical performance? Our first contribution is a theoretical analysis of the Iterative Hard Thresholding (IHT) algorithm when all input data, that is, the measurement matrix and the observation, are quantized aggressively to as little as 2 bits per value. Under reasonable constraints, we show that there exists a variant of low precision IHT that can still provide recovery guarantees. The second contribution is an analysis of our general quantized framework tailored to radio astronomy, showing that its conditions are satisfied in this case. We evaluate our approach using CPU and FPGA implementations, and show that it can achieve up to 9.19x speed up with negligible loss of recovery quality, on real telescope data.

Layerwise Systematic Scan: Deep Boltzmann Machines and Beyond

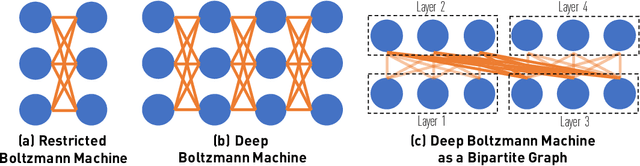
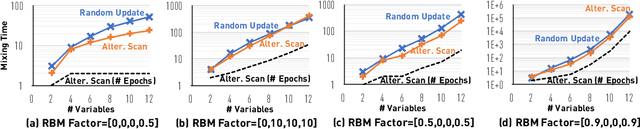
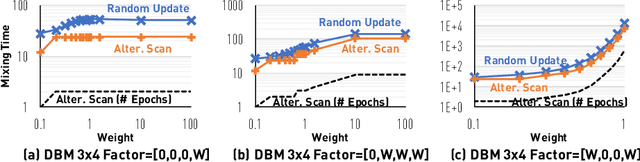
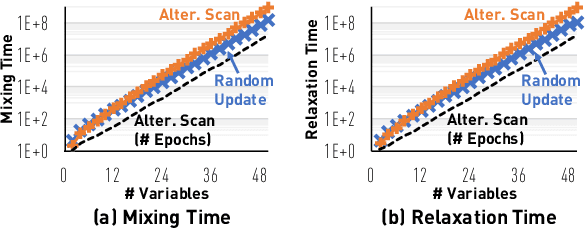
For Markov chain Monte Carlo methods, one of the greatest discrepancies between theory and system is the scan order - while most theoretical development on the mixing time analysis deals with random updates, real-world systems are implemented with systematic scans. We bridge this gap for models that exhibit a bipartite structure, including, most notably, the Restricted/Deep Boltzmann Machine. The de facto implementation for these models scans variables in a layerwise fashion. We show that the Gibbs sampler with a layerwise alternating scan order has its relaxation time (in terms of epochs) no larger than that of a random-update Gibbs sampler (in terms of variable updates). We also construct examples to show that this bound is asymptotically tight. Through standard inequalities, our result also implies a comparison on the mixing times.

The ZipML Framework for Training Models with End-to-End Low Precision: The Cans, the Cannots, and a Little Bit of Deep Learning

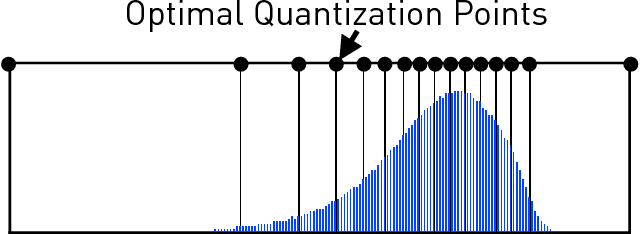
Recently there has been significant interest in training machine-learning models at low precision: by reducing precision, one can reduce computation and communication by one order of magnitude. We examine training at reduced precision, both from a theoretical and practical perspective, and ask: is it possible to train models at end-to-end low precision with provable guarantees? Can this lead to consistent order-of-magnitude speedups? We present a framework called ZipML to answer these questions. For linear models, the answer is yes. We develop a simple framework based on one simple but novel strategy called double sampling. Our framework is able to execute training at low precision with no bias, guaranteeing convergence, whereas naive quantization would introduce significant bias. We validate our framework across a range of applications, and show that it enables an FPGA prototype that is up to 6.5x faster than an implementation using full 32-bit precision. We further develop a variance-optimal stochastic quantization strategy and show that it can make a significant difference in a variety of settings. When applied to linear models together with double sampling, we save up to another 1.7x in data movement compared with uniform quantization. When training deep networks with quantized models, we achieve higher accuracy than the state-of-the-art XNOR-Net. Finally, we extend our framework through approximation to non-linear models, such as SVM. We show that, although using low-precision data induces bias, we can appropriately bound and control the bias. We find in practice 8-bit precision is often sufficient to converge to the correct solution. Interestingly, however, in practice we notice that our framework does not always outperform the naive rounding approach. We discuss this negative result in detail.