Stochastic Gradient Descent without Full Data Shuffle
Paper and Code
Jun 12, 2022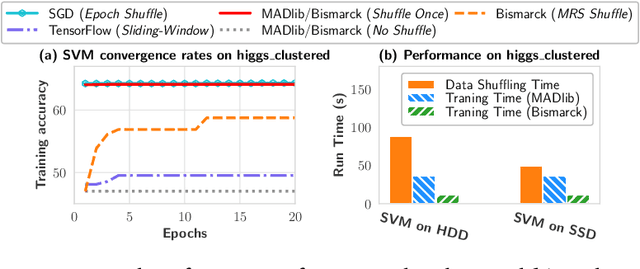

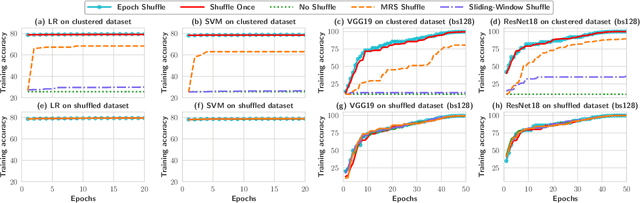
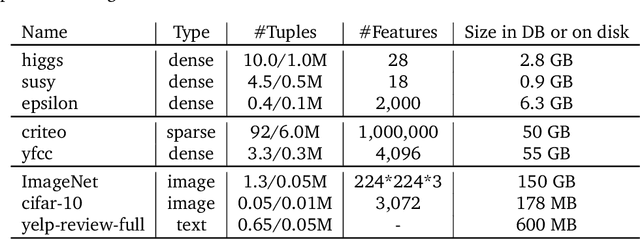
Stochastic gradient descent (SGD) is the cornerstone of modern machine learning (ML) systems. Despite its computational efficiency, SGD requires random data access that is inherently inefficient when implemented in systems that rely on block-addressable secondary storage such as HDD and SSD, e.g., TensorFlow/PyTorch and in-DB ML systems over large files. To address this impedance mismatch, various data shuffling strategies have been proposed to balance the convergence rate of SGD (which favors randomness) and its I/O performance (which favors sequential access). In this paper, we first conduct a systematic empirical study on existing data shuffling strategies, which reveals that all existing strategies have room for improvement -- they all suffer in terms of I/O performance or convergence rate. With this in mind, we propose a simple but novel hierarchical data shuffling strategy, CorgiPile. Compared with existing strategies, CorgiPile avoids a full data shuffle while maintaining comparable convergence rate of SGD as if a full shuffle were performed. We provide a non-trivial theoretical analysis of CorgiPile on its convergence behavior. We further integrate CorgiPile into PyTorch by designing new parallel/distributed shuffle operators inside a new CorgiPileDataSet API. We also integrate CorgiPile into PostgreSQL by introducing three new physical operators with optimizations. Our experimental results show that CorgiPile can achieve comparable convergence rate with the full shuffle based SGD for both deep learning and generalized linear models. For deep learning models on ImageNet dataset, CorgiPile is 1.5X faster than PyTorch with full data shuffle. For in-DB ML with linear models, CorgiPile is 1.6X-12.8X faster than two state-of-the-art in-DB ML systems, Apache MADlib and Bismarck, on both HDD and SSD.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge