JiuZhang3.0: Efficiently Improving Mathematical Reasoning by Training Small Data Synthesis Models

Mathematical reasoning is an important capability of large language models~(LLMs) for real-world applications. To enhance this capability, existing work either collects large-scale math-related texts for pre-training, or relies on stronger LLMs (\eg GPT-4) to synthesize massive math problems. Both types of work generally lead to large costs in training or synthesis. To reduce the cost, based on open-source available texts, we propose an efficient way that trains a small LLM for math problem synthesis, to efficiently generate sufficient high-quality pre-training data. To achieve it, we create a dataset using GPT-4 to distill its data synthesis capability into the small LLM. Concretely, we craft a set of prompts based on human education stages to guide GPT-4, to synthesize problems covering diverse math knowledge and difficulty levels. Besides, we adopt the gradient-based influence estimation method to select the most valuable math-related texts. The both are fed into GPT-4 for creating the knowledge distillation dataset to train the small LLM. We leverage it to synthesize 6 million math problems for pre-training our JiuZhang3.0 model, which only needs to invoke GPT-4 API 9.3k times and pre-train on 4.6B data. Experimental results have shown that JiuZhang3.0 achieves state-of-the-art performance on several mathematical reasoning datasets, under both natural language reasoning and tool manipulation settings. Our code and data will be publicly released in \url{https://github.com/RUCAIBox/JiuZhang3.0}.

Learning to Solve Geometry Problems via Simulating Human Dual-Reasoning Process

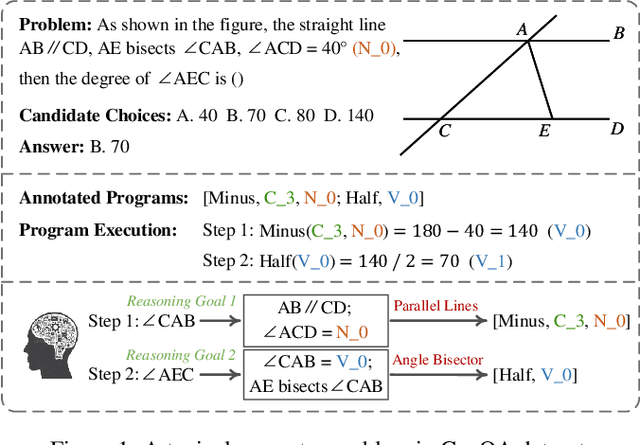
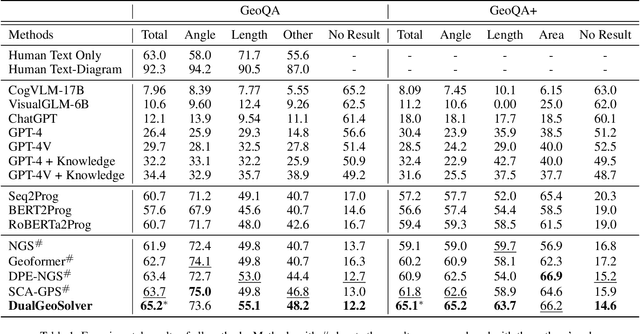
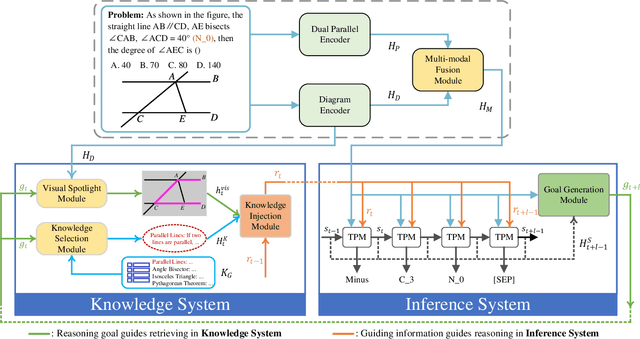
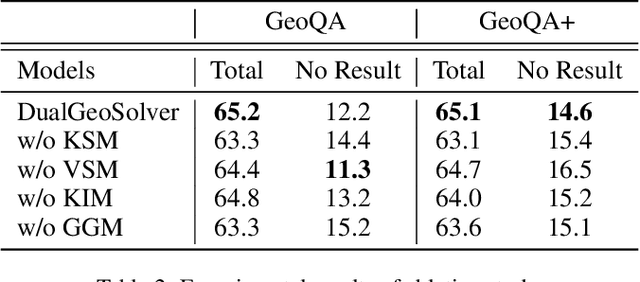
Geometry Problem Solving (GPS), which is a classic and challenging math problem, has attracted much attention in recent years. It requires a solver to comprehensively understand both text and diagram, master essential geometry knowledge, and appropriately apply it in reasoning. However, existing works follow a paradigm of neural machine translation and only focus on enhancing the capability of encoders, which neglects the essential characteristics of human geometry reasoning. In this paper, inspired by dual-process theory, we propose a Dual-Reasoning Geometry Solver (DualGeoSolver) to simulate the dual-reasoning process of humans for GPS. Specifically, we construct two systems in DualGeoSolver, namely Knowledge System and Inference System. Knowledge System controls an implicit reasoning process, which is responsible for providing diagram information and geometry knowledge according to a step-wise reasoning goal generated by Inference System. Inference System conducts an explicit reasoning process, which specifies the goal in each reasoning step and applies the knowledge to generate program tokens for resolving it. The two systems carry out the above process iteratively, which behaves more in line with human cognition. We conduct extensive experiments on two benchmark datasets, GeoQA and GeoQA+. The results demonstrate the superiority of DualGeoSolver in both solving accuracy and robustness from explicitly modeling human reasoning process and knowledge application.

Bit-mask Robust Contrastive Knowledge Distillation for Unsupervised Semantic Hashing

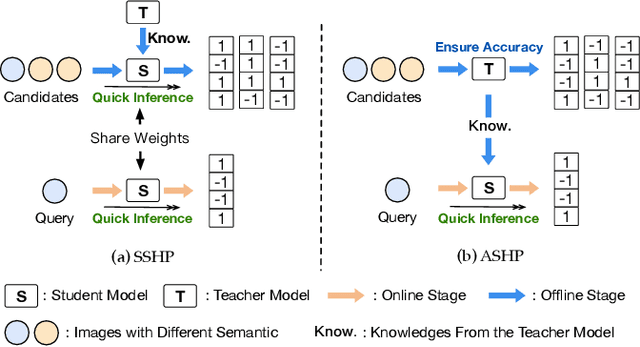
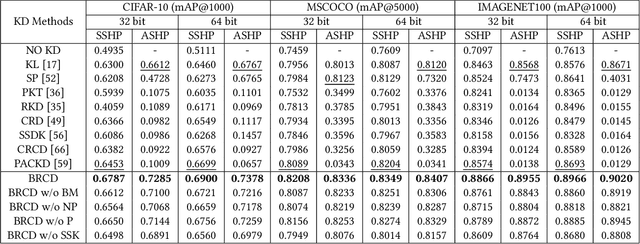
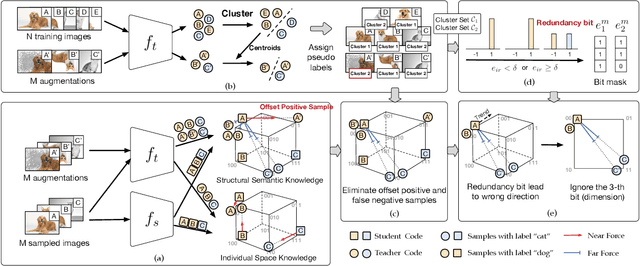
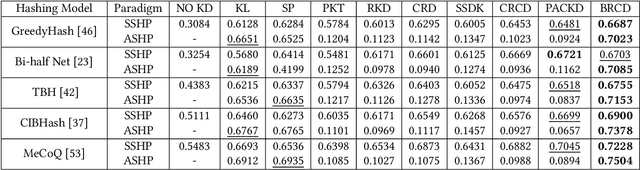
Unsupervised semantic hashing has emerged as an indispensable technique for fast image search, which aims to convert images into binary hash codes without relying on labels. Recent advancements in the field demonstrate that employing large-scale backbones (e.g., ViT) in unsupervised semantic hashing models can yield substantial improvements. However, the inference delay has become increasingly difficult to overlook. Knowledge distillation provides a means for practical model compression to alleviate this delay. Nevertheless, the prevailing knowledge distillation approaches are not explicitly designed for semantic hashing. They ignore the unique search paradigm of semantic hashing, the inherent necessities of the distillation process, and the property of hash codes. In this paper, we propose an innovative Bit-mask Robust Contrastive knowledge Distillation (BRCD) method, specifically devised for the distillation of semantic hashing models. To ensure the effectiveness of two kinds of search paradigms in the context of semantic hashing, BRCD first aligns the semantic spaces between the teacher and student models through a contrastive knowledge distillation objective. Additionally, to eliminate noisy augmentations and ensure robust optimization, a cluster-based method within the knowledge distillation process is introduced. Furthermore, through a bit-level analysis, we uncover the presence of redundancy bits resulting from the bit independence property. To mitigate these effects, we introduce a bit mask mechanism in our knowledge distillation objective. Finally, extensive experiments not only showcase the noteworthy performance of our BRCD method in comparison to other knowledge distillation methods but also substantiate the generality of our methods across diverse semantic hashing models and backbones. The code for BRCD is available at https://github.com/hly1998/BRCD.

JiuZhang 2.0: A Unified Chinese Pre-trained Language Model for Multi-task Mathematical Problem Solving

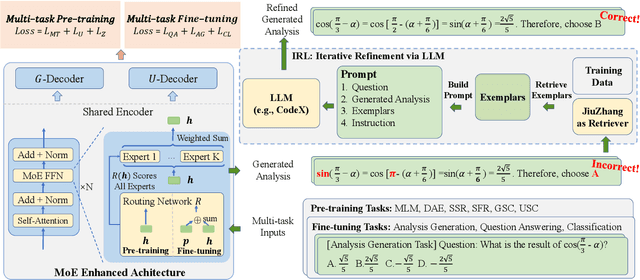
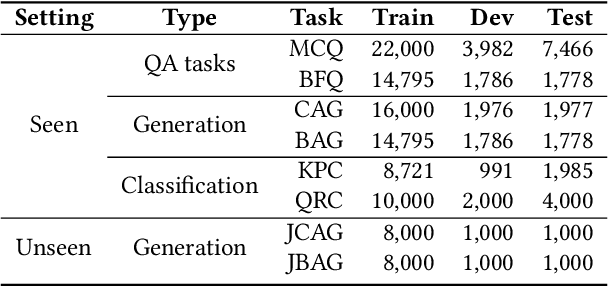
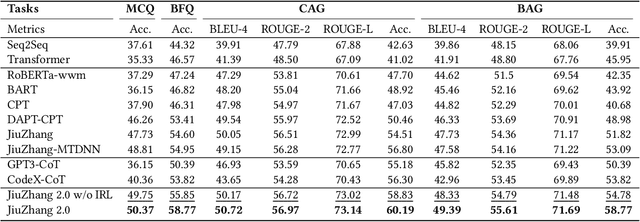
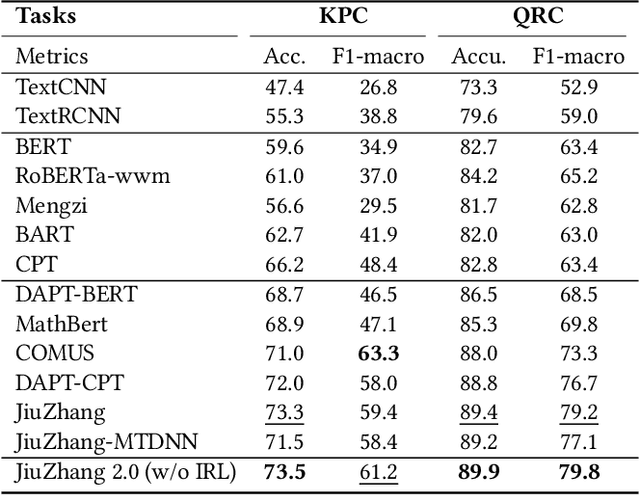
Although pre-trained language models~(PLMs) have recently advanced the research progress in mathematical reasoning, they are not specially designed as a capable multi-task solver, suffering from high cost for multi-task deployment (\eg a model copy for a task) and inferior performance on complex mathematical problems in practical applications. To address these issues, in this paper, we propose \textbf{JiuZhang~2.0}, a unified Chinese PLM specially for multi-task mathematical problem solving. Our idea is to maintain a moderate-sized model and employ the \emph{cross-task knowledge sharing} to improve the model capacity in a multi-task setting. Specially, we construct a Mixture-of-Experts~(MoE) architecture for modeling mathematical text, so as to capture the common mathematical knowledge across tasks. For optimizing the MoE architecture, we design \emph{multi-task continual pre-training} and \emph{multi-task fine-tuning} strategies for multi-task adaptation. These training strategies can effectively decompose the knowledge from the task data and establish the cross-task sharing via expert networks. In order to further improve the general capacity of solving different complex tasks, we leverage large language models~(LLMs) as complementary models to iteratively refine the generated solution by our PLM, via in-context learning. Extensive experiments have demonstrated the effectiveness of our model.

Evaluating and Improving Tool-Augmented Computation-Intensive Math Reasoning

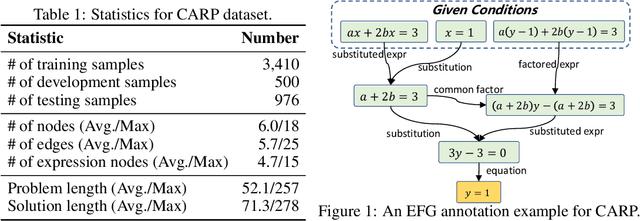
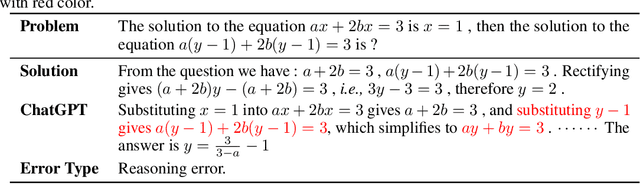
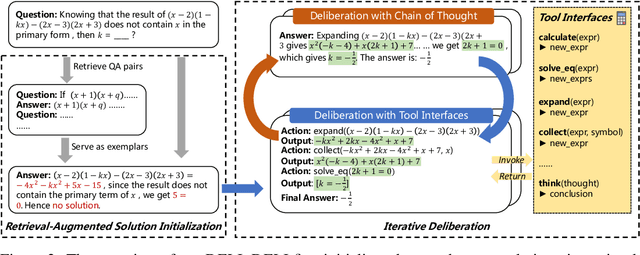
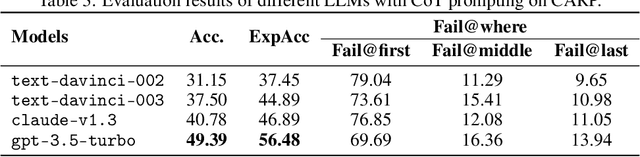
Chain-of-thought prompting~(CoT) and tool augmentation have been validated in recent work as effective practices for improving large language models~(LLMs) to perform step-by-step reasoning on complex math-related tasks. However, most existing math reasoning datasets may be not able to fully evaluate and analyze the ability of LLMs in manipulating tools and performing reasoning, as they may only require very few invocations of tools or miss annotations for evaluating intermediate reasoning steps. To address the issue, we construct \textbf{CARP}, a new Chinese dataset consisting of 4,886 computation-intensive algebra problems with formulated annotations on intermediate steps. In CARP, we test four LLMs with CoT prompting, and find that they are all prone to make mistakes at the early steps of the solution, leading to wrong answers. Based on this finding, we propose a new approach that can deliberate the reasoning steps with tool interfaces, namely \textbf{DELI}. In DELI, we first initialize a step-by-step solution based on retrieved exemplars, then iterate two deliberation procedures that check and refine the intermediate steps of the generated solution, from the perspectives of tool manipulation and natural language reasoning, until obtaining converged solutions or reaching the maximum turn. Experimental results on CARP and six other datasets show that the proposed DELI mostly outperforms competitive baselines, and can further boost the performance of existing CoT methods. Our data and code are available in \url{https://github.com/RUCAIBox/CARP}.

JiuZhang: A Chinese Pre-trained Language Model for Mathematical Problem Understanding

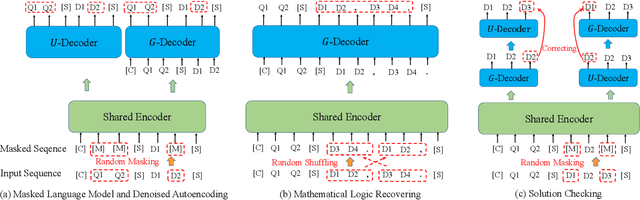
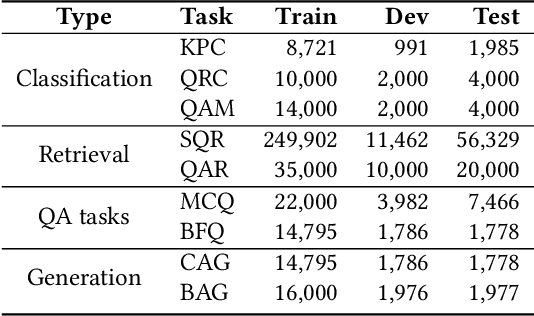
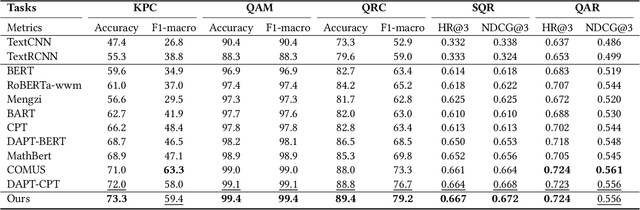
This paper aims to advance the mathematical intelligence of machines by presenting the first Chinese mathematical pre-trained language model~(PLM) for effectively understanding and representing mathematical problems. Unlike other standard NLP tasks, mathematical texts are difficult to understand, since they involve mathematical terminology, symbols and formulas in the problem statement. Typically, it requires complex mathematical logic and background knowledge for solving mathematical problems. Considering the complex nature of mathematical texts, we design a novel curriculum pre-training approach for improving the learning of mathematical PLMs, consisting of both basic and advanced courses. Specially, we first perform token-level pre-training based on a position-biased masking strategy, and then design logic-based pre-training tasks that aim to recover the shuffled sentences and formulas, respectively. Finally, we introduce a more difficult pre-training task that enforces the PLM to detect and correct the errors in its generated solutions. We conduct extensive experiments on offline evaluation (including nine math-related tasks) and online $A/B$ test. Experimental results demonstrate the effectiveness of our approach compared with a number of competitive baselines. Our code is available at: \textcolor{blue}{\url{https://github.com/RUCAIBox/JiuZhang}}.