Contractual Reinforcement Learning: Pulling Arms with Invisible Hands

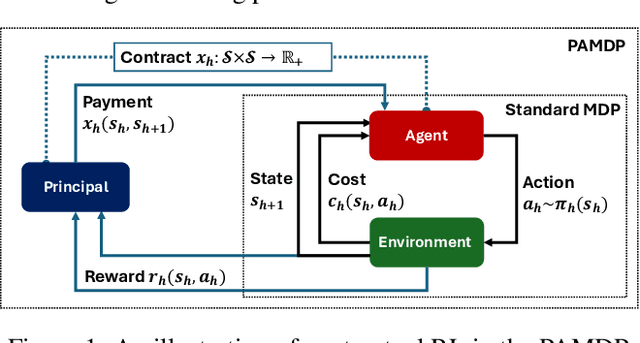
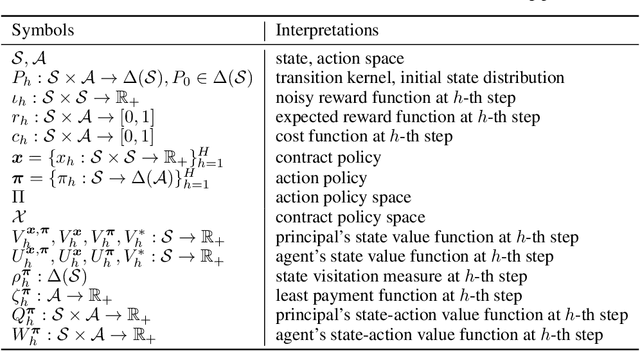
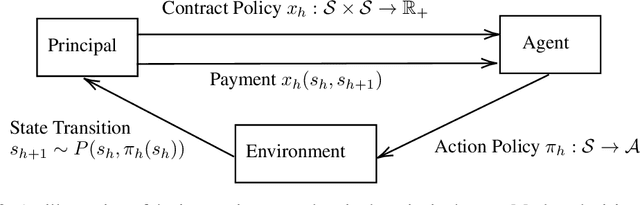
The agency problem emerges in today's large scale machine learning tasks, where the learners are unable to direct content creation or enforce data collection. In this work, we propose a theoretical framework for aligning economic interests of different stakeholders in the online learning problems through contract design. The problem, termed \emph{contractual reinforcement learning}, naturally arises from the classic model of Markov decision processes, where a learning principal seeks to optimally influence the agent's action policy for their common interests through a set of payment rules contingent on the realization of next state. For the planning problem, we design an efficient dynamic programming algorithm to determine the optimal contracts against the far-sighted agent. For the learning problem, we introduce a generic design of no-regret learning algorithms to untangle the challenges from robust design of contracts to the balance of exploration and exploitation, reducing the complexity analysis to the construction of efficient search algorithms. For several natural classes of problems, we design tailored search algorithms that provably achieve $\tilde{O}(\sqrt{T})$ regret. We also present an algorithm with $\tilde{O}(T^{2/3})$ for the general problem that improves the existing analysis in online contract design with mild technical assumptions.

Learning to Incentivize Information Acquisition: Proper Scoring Rules Meet Principal-Agent Model

We study the incentivized information acquisition problem, where a principal hires an agent to gather information on her behalf. Such a problem is modeled as a Stackelberg game between the principal and the agent, where the principal announces a scoring rule that specifies the payment, and then the agent then chooses an effort level that maximizes her own profit and reports the information. We study the online setting of such a problem from the principal's perspective, i.e., designing the optimal scoring rule by repeatedly interacting with the strategic agent. We design a provably sample efficient algorithm that tailors the UCB algorithm (Auer et al., 2002) to our model, which achieves a sublinear $T^{2/3}$-regret after $T$ iterations. Our algorithm features a delicate estimation procedure for the optimal profit of the principal, and a conservative correction scheme that ensures the desired agent's actions are incentivized. Furthermore, a key feature of our regret bound is that it is independent of the number of states of the environment.

Sequential Information Design: Markov Persuasion Process and Its Efficient Reinforcement Learning

In today's economy, it becomes important for Internet platforms to consider the sequential information design problem to align its long term interest with incentives of the gig service providers. This paper proposes a novel model of sequential information design, namely the Markov persuasion processes (MPPs), where a sender, with informational advantage, seeks to persuade a stream of myopic receivers to take actions that maximizes the sender's cumulative utilities in a finite horizon Markovian environment with varying prior and utility functions. Planning in MPPs thus faces the unique challenge in finding a signaling policy that is simultaneously persuasive to the myopic receivers and inducing the optimal long-term cumulative utilities of the sender. Nevertheless, in the population level where the model is known, it turns out that we can efficiently determine the optimal (resp. $\epsilon$-optimal) policy with finite (resp. infinite) states and outcomes, through a modified formulation of the Bellman equation. Our main technical contribution is to study the MPP under the online reinforcement learning (RL) setting, where the goal is to learn the optimal signaling policy by interacting with with the underlying MPP, without the knowledge of the sender's utility functions, prior distributions, and the Markov transition kernels. We design a provably efficient no-regret learning algorithm, the Optimism-Pessimism Principle for Persuasion Process (OP4), which features a novel combination of both optimism and pessimism principles. Our algorithm enjoys sample efficiency by achieving a sublinear $\sqrt{T}$-regret upper bound. Furthermore, both our algorithm and theory can be applied to MPPs with large space of outcomes and states via function approximation, and we showcase such a success under the linear setting.

Multi-Agent Learning for Iterative Dominance Elimination: Formal Barriers and New Algorithms

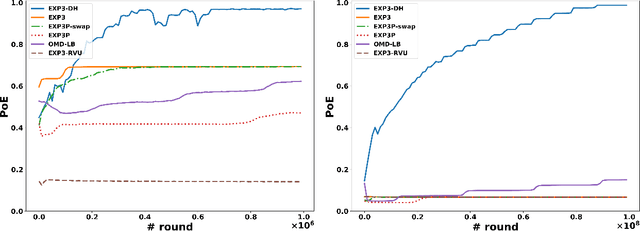
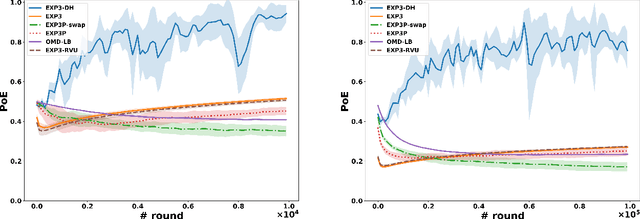
Dominated actions are natural (and perhaps the simplest possible) multi-agent generalizations of sub-optimal actions as in standard single-agent decision making. Thus similar to standard bandit learning, a basic learning question in multi-agent systems is whether agents can learn to efficiently eliminate all dominated actions in an unknown game if they can only observe noisy bandit feedback about the payoff of their played actions. Surprisingly, despite a seemingly simple task, we show a quite negative result; that is, standard no regret algorithms -- including the entire family of Dual Averaging algorithms -- provably take exponentially many rounds to eliminate all dominated actions. Moreover, algorithms with the stronger no swap regret also suffer similar exponential inefficiency. To overcome these barriers, we develop a new algorithm that adjusts Exp3 with Diminishing Historical rewards (termed Exp3-DH); Exp3-DH gradually forgets history at carefully tailored rates. We prove that when all agents run Exp3-DH (a.k.a., self-play in multi-agent learning), all dominated actions can be iteratively eliminated within polynomially many rounds. Our experimental results further demonstrate the efficiency of Exp3-DH, and that state-of-the-art bandit algorithms, even those developed specifically for learning in games, fail to eliminate all dominated actions efficiently.

Least Square Calibration for Peer Review

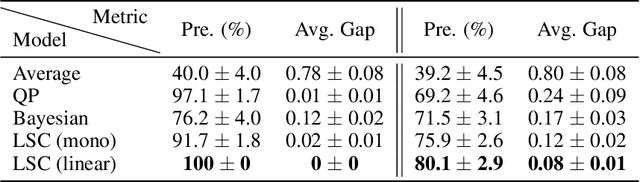
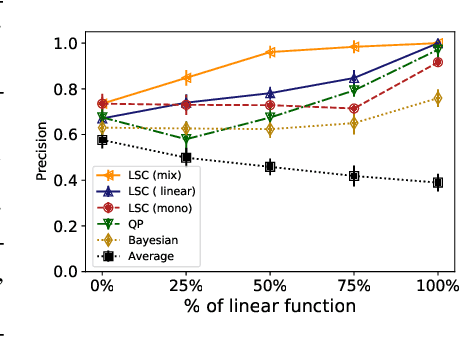
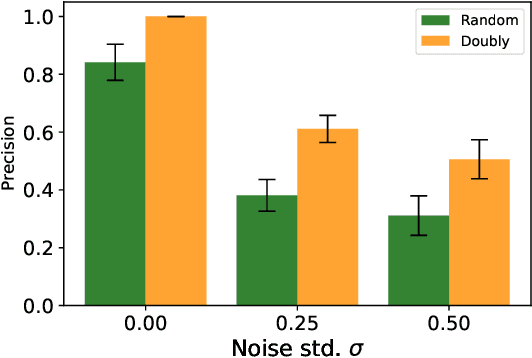
Peer review systems such as conference paper review often suffer from the issue of miscalibration. Previous works on peer review calibration usually only use the ordinal information or assume simplistic reviewer scoring functions such as linear functions. In practice, applications like academic conferences often rely on manual methods, such as open discussions, to mitigate miscalibration. It remains an important question to develop algorithms that can handle different types of miscalibrations based on available prior knowledge. In this paper, we propose a flexible framework, namely least square calibration (LSC), for selecting top candidates from peer ratings. Our framework provably performs perfect calibration from noiseless linear scoring functions under mild assumptions, yet also provides competitive calibration results when the scoring function is from broader classes beyond linear functions and with arbitrary noise. On our synthetic dataset, we empirically demonstrate that our algorithm consistently outperforms the baseline which select top papers based on the highest average ratings.

Déjà vu: A Contextualized Temporal Attention Mechanism for Sequential Recommendation

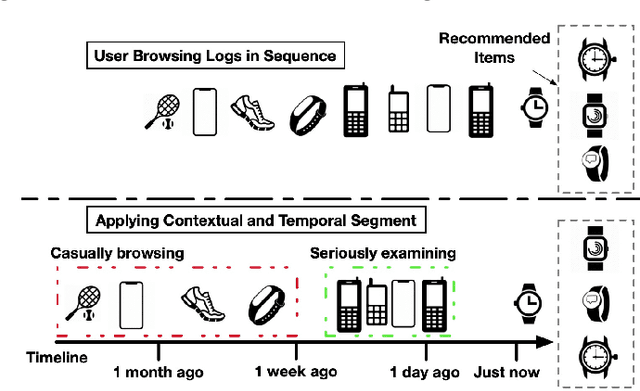
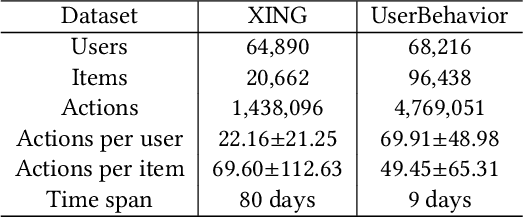
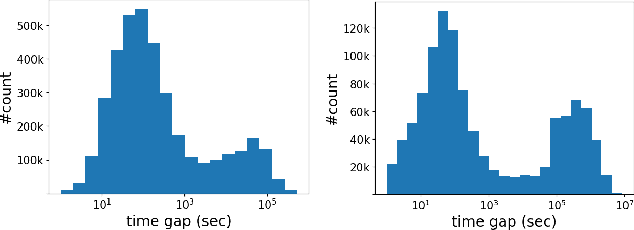
Predicting users' preferences based on their sequential behaviors in history is challenging and crucial for modern recommender systems. Most existing sequential recommendation algorithms focus on transitional structure among the sequential actions, but largely ignore the temporal and context information, when modeling the influence of a historical event to current prediction. In this paper, we argue that the influence from the past events on a user's current action should vary over the course of time and under different context. Thus, we propose a Contextualized Temporal Attention Mechanism that learns to weigh historical actions' influence on not only what action it is, but also when and how the action took place. More specifically, to dynamically calibrate the relative input dependence from the self-attention mechanism, we deploy multiple parameterized kernel functions to learn various temporal dynamics, and then use the context information to determine which of these reweighing kernels to follow for each input. In empirical evaluations on two large public recommendation datasets, our model consistently outperformed an extensive set of state-of-the-art sequential recommendation methods.