Xiaohui Bei
Least Square Calibration for Peer Review
Oct 25, 2021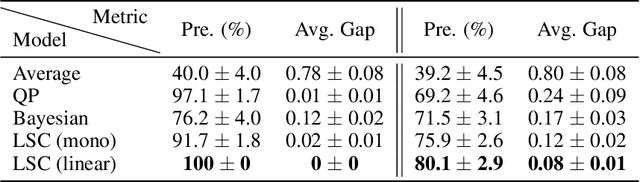
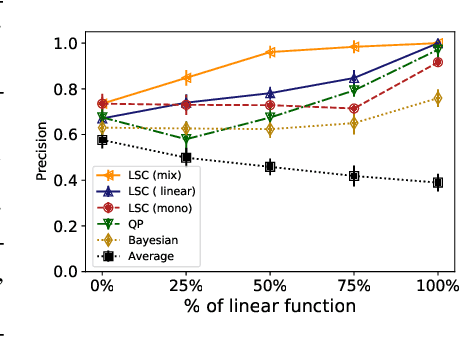

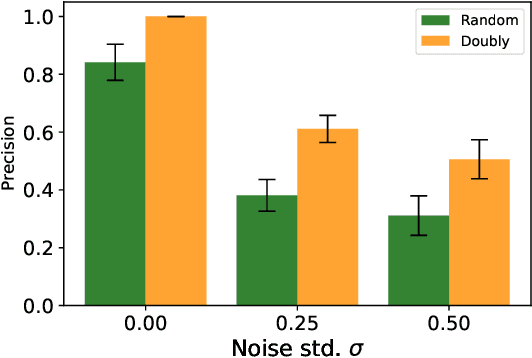
Abstract:Peer review systems such as conference paper review often suffer from the issue of miscalibration. Previous works on peer review calibration usually only use the ordinal information or assume simplistic reviewer scoring functions such as linear functions. In practice, applications like academic conferences often rely on manual methods, such as open discussions, to mitigate miscalibration. It remains an important question to develop algorithms that can handle different types of miscalibrations based on available prior knowledge. In this paper, we propose a flexible framework, namely least square calibration (LSC), for selecting top candidates from peer ratings. Our framework provably performs perfect calibration from noiseless linear scoring functions under mild assumptions, yet also provides competitive calibration results when the scoring function is from broader classes beyond linear functions and with arbitrary noise. On our synthetic dataset, we empirically demonstrate that our algorithm consistently outperforms the baseline which select top papers based on the highest average ratings.
Dynamic Trip-Vehicle Dispatch with Scheduled and On-Demand Requests
Jul 20, 2019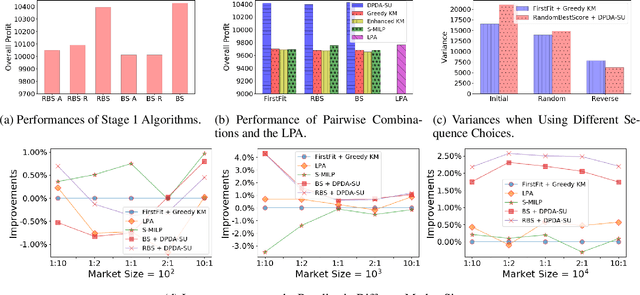
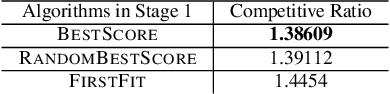
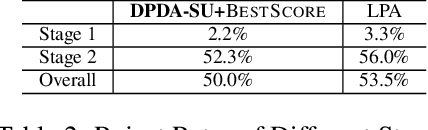
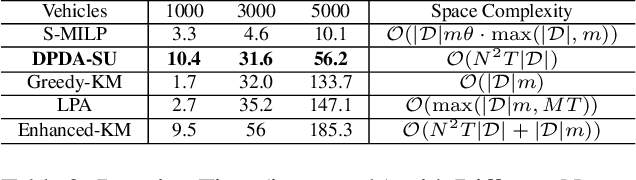
Abstract:Transportation service providers that dispatch drivers and vehicles to riders start to support both on-demand ride requests posted in real time and rides scheduled in advance, leading to new challenges which, to the best of our knowledge, have not been addressed by existing works. To fill the gap, we design novel trip-vehicle dispatch algorithms to handle both types of requests while taking into account an estimated request distribution of on-demand requests. At the core of the algorithms is the newly proposed Constrained Spatio-Temporal value function (CST-function), which is polynomial-time computable and represents the expected value a vehicle could gain with the constraint that it needs to arrive at a specific location at a given time. Built upon CST-function, we design a randomized best-fit algorithm for scheduled requests and an online planning algorithm for on-demand requests given the scheduled requests as constraints. We evaluate the algorithms through extensive experiments on a real-world dataset of an online ride-hailing platform.
Networked Fairness in Cake Cutting
Jul 07, 2017
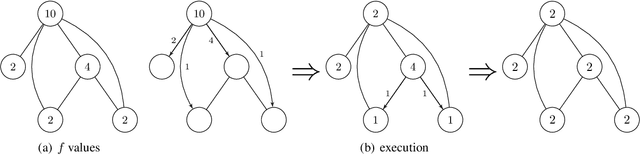
Abstract:We introduce a graphical framework for fair division in cake cutting, where comparisons between agents are limited by an underlying network structure. We generalize the classical fairness notions of envy-freeness and proportionality to this graphical setting. Given a simple undirected graph G, an allocation is envy-free on G if no agent envies any of her neighbor's share, and is proportional on G if every agent values her own share no less than the average among her neighbors, with respect to her own measure. These generalizations open new research directions in developing simple and efficient algorithms that can produce fair allocations under specific graph structures. On the algorithmic frontier, we first propose a moving-knife algorithm that outputs an envy-free allocation on trees. The algorithm is significantly simpler than the discrete and bounded envy-free algorithm recently designed by Aziz and Mackenzie for complete graphs. Next, we give a discrete and bounded algorithm for computing a proportional allocation on descendant graphs, a class of graphs by taking a rooted tree and connecting all its ancestor-descendant pairs.
On the Complexity of Trial and Error
Apr 18, 2013Abstract:Motivated by certain applications from physics, biochemistry, economics, and computer science, in which the objects under investigation are not accessible because of various limitations, we propose a trial-and-error model to examine algorithmic issues in such situations. Given a search problem with a hidden input, we are asked to find a valid solution, to find which we can propose candidate solutions (trials), and use observed violations (errors), to prepare future proposals. In accordance with our motivating applications, we consider the fairly broad class of constraint satisfaction problems, and assume that errors are signaled by a verification oracle in the format of the index of a violated constraint (with the content of the constraint still hidden). Our discoveries are summarized as follows. On one hand, despite the seemingly very little information provided by the verification oracle, efficient algorithms do exist for a number of important problems. For the Nash, Core, Stable Matching, and SAT problems, the unknown-input versions are as hard as the corresponding known-input versions, up to a factor of polynomial. We further give almost tight bounds on the latter two problems' trial complexities. On the other hand, there are problems whose complexities are substantially increased in the unknown-input model. In particular, no time-efficient algorithms exist (under standard hardness assumptions) for Graph Isomorphism and Group Isomorphism problems. The tools used to achieve these results include order theory, strong ellipsoid method, and some non-standard reductions. Our model investigates the value of information, and our results demonstrate that the lack of input information can introduce various levels of extra difficulty. The model exhibits intimate connections with (and we hope can also serve as a useful supplement to) certain existing learning and complexity theories.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge