Multi-Agent Learning for Iterative Dominance Elimination: Formal Barriers and New Algorithms
Paper and Code
Nov 10, 2021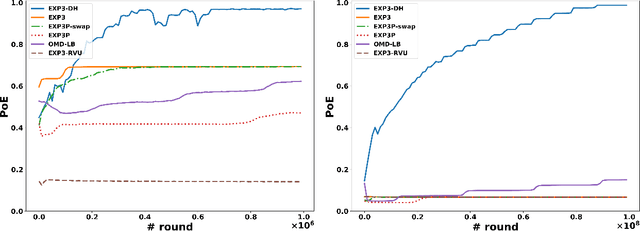
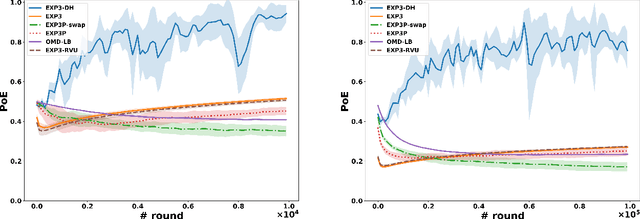
Dominated actions are natural (and perhaps the simplest possible) multi-agent generalizations of sub-optimal actions as in standard single-agent decision making. Thus similar to standard bandit learning, a basic learning question in multi-agent systems is whether agents can learn to efficiently eliminate all dominated actions in an unknown game if they can only observe noisy bandit feedback about the payoff of their played actions. Surprisingly, despite a seemingly simple task, we show a quite negative result; that is, standard no regret algorithms -- including the entire family of Dual Averaging algorithms -- provably take exponentially many rounds to eliminate all dominated actions. Moreover, algorithms with the stronger no swap regret also suffer similar exponential inefficiency. To overcome these barriers, we develop a new algorithm that adjusts Exp3 with Diminishing Historical rewards (termed Exp3-DH); Exp3-DH gradually forgets history at carefully tailored rates. We prove that when all agents run Exp3-DH (a.k.a., self-play in multi-agent learning), all dominated actions can be iteratively eliminated within polynomially many rounds. Our experimental results further demonstrate the efficiency of Exp3-DH, and that state-of-the-art bandit algorithms, even those developed specifically for learning in games, fail to eliminate all dominated actions efficiently.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge