Contractual Reinforcement Learning: Pulling Arms with Invisible Hands
Paper and Code
Jul 02, 2024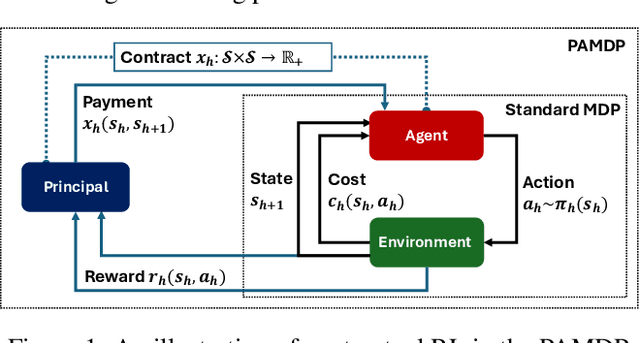

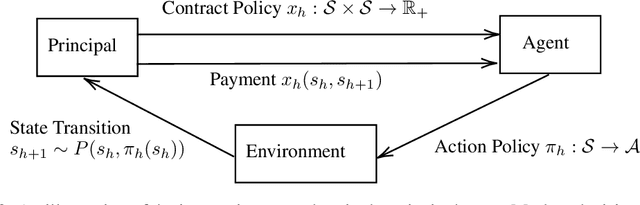
The agency problem emerges in today's large scale machine learning tasks, where the learners are unable to direct content creation or enforce data collection. In this work, we propose a theoretical framework for aligning economic interests of different stakeholders in the online learning problems through contract design. The problem, termed \emph{contractual reinforcement learning}, naturally arises from the classic model of Markov decision processes, where a learning principal seeks to optimally influence the agent's action policy for their common interests through a set of payment rules contingent on the realization of next state. For the planning problem, we design an efficient dynamic programming algorithm to determine the optimal contracts against the far-sighted agent. For the learning problem, we introduce a generic design of no-regret learning algorithms to untangle the challenges from robust design of contracts to the balance of exploration and exploitation, reducing the complexity analysis to the construction of efficient search algorithms. For several natural classes of problems, we design tailored search algorithms that provably achieve $\tilde{O}(\sqrt{T})$ regret. We also present an algorithm with $\tilde{O}(T^{2/3})$ for the general problem that improves the existing analysis in online contract design with mild technical assumptions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge