A Theoretical Analysis of Mamba's Training Dynamics: Filtering Relevant Features for Generalization in State Space Models

The recent empirical success of Mamba and other selective state space models (SSMs) has renewed interest in non-attention architectures for sequence modeling, yet their theoretical foundations remain underexplored. We present a first-step analysis of generalization and learning dynamics for a simplified but representative Mamba block: a single-layer, single-head selective SSM with input-dependent gating, followed by a two-layer MLP trained via gradient descent (GD). Our study adopts a structured data model with tokens that include both class-relevant and class-irrelevant patterns under token-level noise and examines two canonical regimes: majority-voting and locality-structured data sequences. We prove that the model achieves guaranteed generalization by establishing non-asymptotic sample complexity and convergence rate bounds, which improve as the effective signal increases and the noise decreases. Furthermore, we show that the gating vector aligns with class-relevant features while ignoring irrelevant ones, thereby formalizing a feature-selection role similar to attention but realized through selective recurrence. Numerical experiments on synthetic data justify our theoretical results. Overall, our results provide principled insight into when and why Mamba-style selective SSMs learn efficiently, offering a theoretical counterpoint to Transformer-centric explanations.

Merging Smarter, Generalizing Better: Enhancing Model Merging on OOD Data

Multi-task learning (MTL) concurrently trains a model on diverse task datasets to exploit common features, thereby improving overall performance across the tasks. Recent studies have dedicated efforts to merging multiple independent model parameters into a unified model for MTL, thus circumventing the need for training data and expanding the scope of applicable scenarios of MTL. However, current approaches to model merging predominantly concentrate on enhancing performance within in-domain (ID) datasets, often overlooking their efficacy on out-of-domain (OOD) datasets. In this work, we proposed LwPTV (Layer-wise Pruning Task Vector) by building a saliency score, measuring the redundancy of parameters in task vectors. Designed in this way ours can achieve mask vector for each task and thus perform layer-wise pruning on the task vectors, only keeping the pre-trained model parameters at the corresponding layer in merged model. Owing to its flexibility, our method can be seamlessly integrated with most of existing model merging methods to improve their performance on OOD tasks. Extensive experiments demonstrate that the application of our method results in substantial enhancements in OOD performance while preserving the ability on ID tasks.

When is Task Vector Provably Effective for Model Editing? A Generalization Analysis of Nonlinear Transformers

Task arithmetic refers to editing the pre-trained model by adding a weighted sum of task vectors, each of which is the weight update from the pre-trained model to fine-tuned models for certain tasks. This approach recently gained attention as a computationally efficient inference method for model editing, e.g., multi-task learning, forgetting, and out-of-domain generalization capabilities. However, the theoretical understanding of why task vectors can execute various conceptual operations remains limited, due to the highly non-convexity of training Transformer-based models. To the best of our knowledge, this paper provides the first theoretical characterization of the generalization guarantees of task vector methods on nonlinear Transformers. We consider a conceptual learning setting, where each task is a binary classification problem based on a discriminative pattern. We theoretically prove the effectiveness of task addition in simultaneously learning a set of irrelevant or aligned tasks, as well as the success of task negation in unlearning one task from irrelevant or contradictory tasks. Moreover, we prove the proper selection of linear coefficients for task arithmetic to achieve guaranteed generalization to out-of-domain tasks. All of our theoretical results hold for both dense-weight parameters and their low-rank approximations. Although established in a conceptual setting, our theoretical findings were validated on a practical machine unlearning task using the large language model Phi-1.5 (1.3B).

Training Nonlinear Transformers for Chain-of-Thought Inference: A Theoretical Generalization Analysis

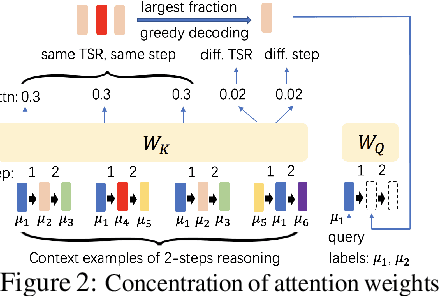
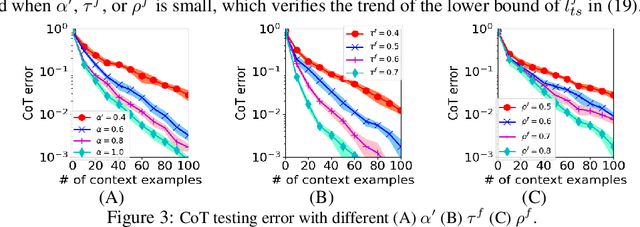
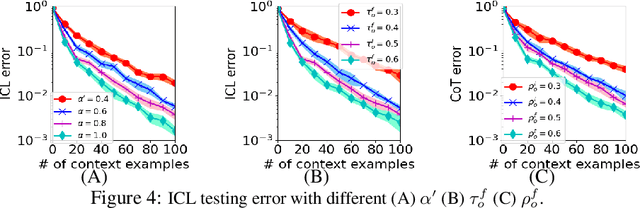
Chain-of-Thought (CoT) is an efficient prompting method that enables the reasoning ability of large language models by augmenting the query using multiple examples with multiple intermediate steps. Despite the empirical success, the theoretical understanding of how to train a Transformer to achieve the CoT ability remains less explored. This is primarily due to the technical challenges involved in analyzing the nonconvex optimization on nonlinear attention models. To the best of our knowledge, this work provides the first theoretical study of training Transformers with nonlinear attention to obtain the CoT generalization capability so that the resulting model can inference on unseen tasks when the input is augmented by examples of the new task. We first quantify the required training samples and iterations to train a Transformer model towards CoT ability. We then prove the success of its CoT generalization on unseen tasks with distribution-shifted testing data. Moreover, we theoretically characterize the conditions for an accurate reasoning output by CoT even when the provided reasoning examples contain noises and are not always accurate. In contrast, in-context learning (ICL), which can be viewed as one-step CoT without intermediate steps, may fail to provide an accurate output when CoT does. These theoretical findings are justified through experiments.

Learning on Transformers is Provable Low-Rank and Sparse: A One-layer Analysis

Efficient training and inference algorithms, such as low-rank adaption and model pruning, have shown impressive performance for learning Transformer-based large foundation models. However, due to the technical challenges of the non-convex optimization caused by the complicated architecture of Transformers, the theoretical study of why these methods can be applied to learn Transformers is mostly elusive. To the best of our knowledge, this paper shows the first theoretical analysis of the property of low-rank and sparsity of one-layer Transformers by characterizing the trained model after convergence using stochastic gradient descent. By focusing on a data model based on label-relevant and label-irrelevant patterns, we quantify that the gradient updates of trainable parameters are low-rank, which depends on the number of label-relevant patterns. We also analyze how model pruning affects the generalization while improving computation efficiency and conclude that proper magnitude-based pruning has a slight effect on the testing performance. We implement numerical experiments to support our findings.

What Improves the Generalization of Graph Transformers? A Theoretical Dive into the Self-attention and Positional Encoding

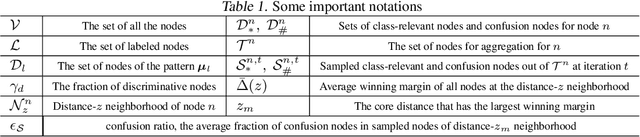
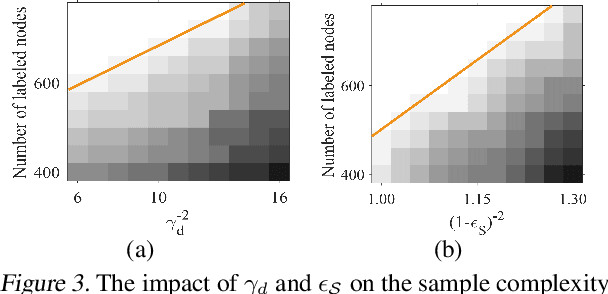
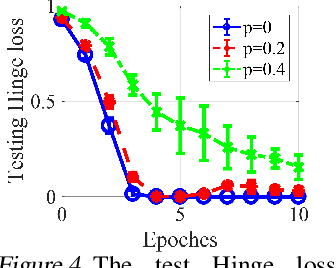
Graph Transformers, which incorporate self-attention and positional encoding, have recently emerged as a powerful architecture for various graph learning tasks. Despite their impressive performance, the complex non-convex interactions across layers and the recursive graph structure have made it challenging to establish a theoretical foundation for learning and generalization. This study introduces the first theoretical investigation of a shallow Graph Transformer for semi-supervised node classification, comprising a self-attention layer with relative positional encoding and a two-layer perceptron. Focusing on a graph data model with discriminative nodes that determine node labels and non-discriminative nodes that are class-irrelevant, we characterize the sample complexity required to achieve a desirable generalization error by training with stochastic gradient descent (SGD). This paper provides the quantitative characterization of the sample complexity and number of iterations for convergence dependent on the fraction of discriminative nodes, the dominant patterns, and the initial model errors. Furthermore, we demonstrate that self-attention and positional encoding enhance generalization by making the attention map sparse and promoting the core neighborhood during training, which explains the superior feature representation of Graph Transformers. Our theoretical results are supported by empirical experiments on synthetic and real-world benchmarks.

How does promoting the minority fraction affect generalization? A theoretical study of the one-hidden-layer neural network on group imbalance

Group imbalance has been a known problem in empirical risk minimization (ERM), where the achieved high average accuracy is accompanied by low accuracy in a minority group. Despite algorithmic efforts to improve the minority group accuracy, a theoretical generalization analysis of ERM on individual groups remains elusive. By formulating the group imbalance problem with the Gaussian Mixture Model, this paper quantifies the impact of individual groups on the sample complexity, the convergence rate, and the average and group-level testing performance. Although our theoretical framework is centered on binary classification using a one-hidden-layer neural network, to the best of our knowledge, we provide the first theoretical analysis of the group-level generalization of ERM in addition to the commonly studied average generalization performance. Sample insights of our theoretical results include that when all group-level co-variance is in the medium regime and all mean are close to zero, the learning performance is most desirable in the sense of a small sample complexity, a fast training rate, and a high average and group-level testing accuracy. Moreover, we show that increasing the fraction of the minority group in the training data does not necessarily improve the generalization performance of the minority group. Our theoretical results are validated on both synthetic and empirical datasets, such as CelebA and CIFAR-10 in image classification.

Training Nonlinear Transformers for Efficient In-Context Learning: A Theoretical Learning and Generalization Analysis

Transformer-based large language models have displayed impressive in-context learning capabilities, where a pre-trained model can handle new tasks without fine-tuning by simply augmenting the query with some input-output examples from that task. Despite the empirical success, the mechanics of how to train a Transformer to achieve ICL and the corresponding ICL capacity is mostly elusive due to the technical challenges of analyzing the nonconvex training problems resulting from the nonlinear self-attention and nonlinear activation in Transformers. To the best of our knowledge, this paper provides the first theoretical analysis of the training dynamics of Transformers with nonlinear self-attention and nonlinear MLP, together with the ICL generalization capability of the resulting model. Focusing on a group of binary classification tasks, we train Transformers using data from a subset of these tasks and quantify the impact of various factors on the ICL generalization performance on the remaining unseen tasks with and without data distribution shifts. We also analyze how different components in the learned Transformers contribute to the ICL performance. Furthermore, we provide the first theoretical analysis of how model pruning affects the ICL performance and prove that proper magnitude-based pruning can have a minimal impact on ICL while reducing inference costs. These theoretical findings are justified through numerical experiments.

On the Convergence and Sample Complexity Analysis of Deep Q-Networks with $ε$-Greedy Exploration

This paper provides a theoretical understanding of Deep Q-Network (DQN) with the $\varepsilon$-greedy exploration in deep reinforcement learning. Despite the tremendous empirical achievement of the DQN, its theoretical characterization remains underexplored. First, the exploration strategy is either impractical or ignored in the existing analysis. Second, in contrast to conventional Q-learning algorithms, the DQN employs the target network and experience replay to acquire an unbiased estimation of the mean-square Bellman error (MSBE) utilized in training the Q-network. However, the existing theoretical analysis of DQNs lacks convergence analysis or bypasses the technical challenges by deploying a significantly overparameterized neural network, which is not computationally efficient. This paper provides the first theoretical convergence and sample complexity analysis of the practical setting of DQNs with $\epsilon$-greedy policy. We prove an iterative procedure with decaying $\epsilon$ converges to the optimal Q-value function geometrically. Moreover, a higher level of $\epsilon$ values enlarges the region of convergence but slows down the convergence, while the opposite holds for a lower level of $\epsilon$ values. Experiments justify our established theoretical insights on DQNs.

How Can Context Help? Exploring Joint Retrieval of Passage and Personalized Context

The integration of external personalized context information into document-grounded conversational systems has significant potential business value, but has not been well-studied. Motivated by the concept of personalized context-aware document-grounded conversational systems, we introduce the task of context-aware passage retrieval. We also construct a dataset specifically curated for this purpose. We describe multiple baseline systems to address this task, and propose a novel approach, Personalized Context-Aware Search (PCAS), that effectively harnesses contextual information during passage retrieval. Experimental evaluations conducted on multiple popular dense retrieval systems demonstrate that our proposed approach not only outperforms the baselines in retrieving the most relevant passage but also excels at identifying the pertinent context among all the available contexts. We envision that our contributions will serve as a catalyst for inspiring future research endeavors in this promising direction.