What Improves the Generalization of Graph Transformers? A Theoretical Dive into the Self-attention and Positional Encoding
Paper and Code
Jun 04, 2024
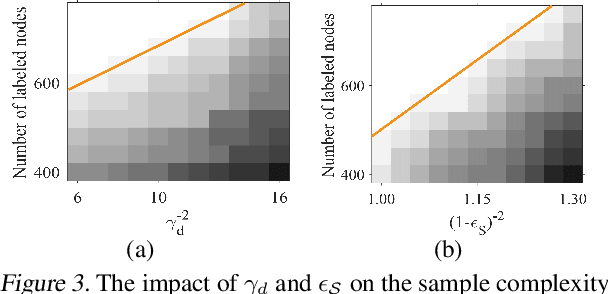
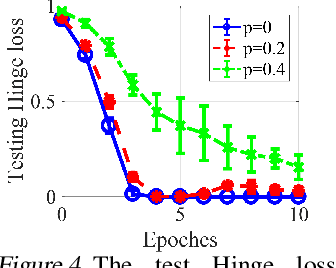
Graph Transformers, which incorporate self-attention and positional encoding, have recently emerged as a powerful architecture for various graph learning tasks. Despite their impressive performance, the complex non-convex interactions across layers and the recursive graph structure have made it challenging to establish a theoretical foundation for learning and generalization. This study introduces the first theoretical investigation of a shallow Graph Transformer for semi-supervised node classification, comprising a self-attention layer with relative positional encoding and a two-layer perceptron. Focusing on a graph data model with discriminative nodes that determine node labels and non-discriminative nodes that are class-irrelevant, we characterize the sample complexity required to achieve a desirable generalization error by training with stochastic gradient descent (SGD). This paper provides the quantitative characterization of the sample complexity and number of iterations for convergence dependent on the fraction of discriminative nodes, the dominant patterns, and the initial model errors. Furthermore, we demonstrate that self-attention and positional encoding enhance generalization by making the attention map sparse and promoting the core neighborhood during training, which explains the superior feature representation of Graph Transformers. Our theoretical results are supported by empirical experiments on synthetic and real-world benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge