DDGM: Solving inverse problems by Diffusive Denoising of Gradient-based Minimization

Inverse problems generally require a regularizer or prior for a good solution. A recent trend is to train a convolutional net to denoise images, and use this net as a prior when solving the inverse problem. Several proposals depend on a singular value decomposition of the forward operator, and several others backpropagate through the denoising net at runtime. Here we propose a simpler approach that combines the traditional gradient-based minimization of reconstruction error with denoising. Noise is also added at each step, so the iterative dynamics resembles a Langevin or diffusion process. Both the level of added noise and the size of the denoising step decay exponentially with time. We apply our method to the problem of tomographic reconstruction from electron micrographs acquired at multiple tilt angles. With empirical studies using simulated tilt views, we find parameter settings for our method that produce good results. We show that high accuracy can be achieved with as few as 50 denoising steps. We also compare with DDRM and DPS, more complex diffusion methods of the kinds mentioned above. These methods are less accurate (as measured by MSE and SSIM) for our tomography problem, even after the generation hyperparameters are optimized. Finally we extend our method to reconstruction of arbitrary-sized images and show results on 128 $\times$ 1568 pixel images

Stacked unsupervised learning with a network architecture found by supervised meta-learning

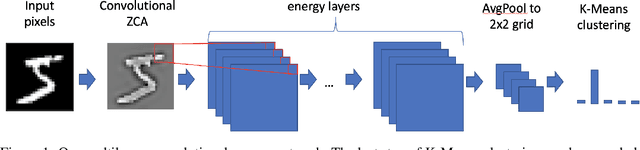
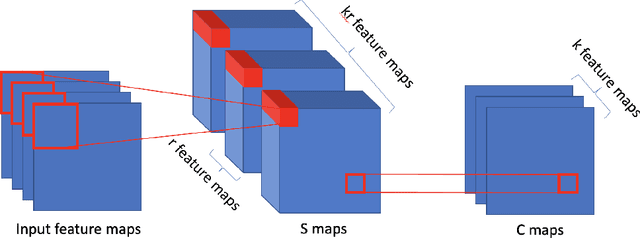
Stacked unsupervised learning (SUL) seems more biologically plausible than backpropagation, because learning is local to each layer. But SUL has fallen far short of backpropagation in practical applications, undermining the idea that SUL can explain how brains learn. Here we show an SUL algorithm that can perform completely unsupervised clustering of MNIST digits with comparable accuracy relative to unsupervised algorithms based on backpropagation. Our algorithm is exceeded only by self-supervised methods requiring training data augmentation by geometric distortions. The only prior knowledge in our unsupervised algorithm is implicit in the network architecture. Multiple convolutional "energy layers" contain a sum-of-squares nonlinearity, inspired by "energy models" of primary visual cortex. Convolutional kernels are learned with a fast minibatch implementation of the K-Subspaces algorithm. High accuracy requires preprocessing with an initial whitening layer, representations that are less sparse during inference than learning, and rescaling for gain control. The hyperparameters of the network architecture are found by supervised meta-learning, which optimizes unsupervised clustering accuracy. We regard such dependence of unsupervised learning on prior knowledge implicit in network architecture as biologically plausible, and analogous to the dependence of brain architecture on evolutionary history.

Kernel similarity matching with Hebbian neural networks

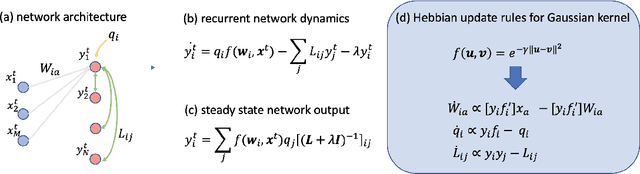
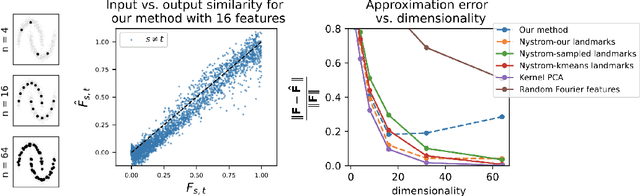
Recent works have derived neural networks with online correlation-based learning rules to perform \textit{kernel similarity matching}. These works applied existing linear similarity matching algorithms to nonlinear features generated with random Fourier methods. In this paper attempt to perform kernel similarity matching by directly learning the nonlinear features. Our algorithm proceeds by deriving and then minimizing an upper bound for the sum of squared errors between output and input kernel similarities. The construction of our upper bound leads to online correlation-based learning rules which can be implemented with a 1 layer recurrent neural network. In addition to generating high-dimensional linearly separable representations, we show that our upper bound naturally yields representations which are sparse and selective for specific input patterns. We compare the approximation quality of our method to neural random Fourier method and variants of the popular but non-biological "Nystr{\"o}m" method for approximating the kernel matrix. Our method appears to be comparable or better than randomly sampled Nystr{\"o}m methods when the outputs are relatively low dimensional (although still potentially higher dimensional than the inputs) but less faithful when the outputs are very high dimensional.

Sensitivity of sparse codes to image distortions

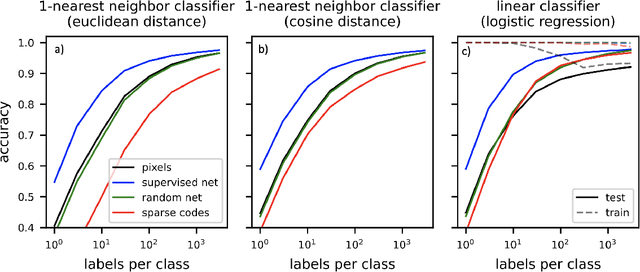
Sparse coding has been proposed as a theory of visual cortex and as an unsupervised algorithm for learning representations. We show empirically with the MNIST dataset that sparse codes can be very sensitive to image distortions, a behavior that may hinder invariant object recognition. A locally linear analysis suggests that the sensitivity is due to the existence of linear combinations of active dictionary elements with high cancellation. A nearest neighbor classifier is shown to perform worse on sparse codes than original images. For a linear classifier with a sufficiently large number of labeled examples, sparse codes are shown to yield higher accuracy than original images, but no higher than a representation computed by a random feedforward net. Sensitivity to distortions seems to be a basic property of sparse codes, and one should be aware of this property when applying sparse codes to invariant object recognition.

Large-scale image segmentation based on distributed clustering algorithms

Many approaches to 3D image segmentation are based on hierarchical clustering of supervoxels into image regions. Here we describe a distributed algorithm capable of handling a tremendous number of supervoxels. The algorithm works recursively, the regions are divided into chunks that are processed independently in parallel by multiple workers. At each round of the recursive procedure, the chunk size in all dimensions are doubled until a single chunk encompasses the entire image. The final result is provably independent of the chunking scheme, and the same as if the entire image were processed without division into chunks. This is nontrivial because a pair of adjacent regions is scored by some statistical property (e.g. mean or median) of the affinities at the interface, and the interface may extend over arbitrarily many chunks. The trick is to delay merge decisions for regions that touch chunk boundaries, and only complete them in a later round after the regions are fully contained within a chunk. We demonstrate the algorithm by clustering an affinity graph with over 1.5 trillion edges between 135 billion supervoxels derived from a 3D electron microscopic brain image.

Learning Dense Voxel Embeddings for 3D Neuron Reconstruction

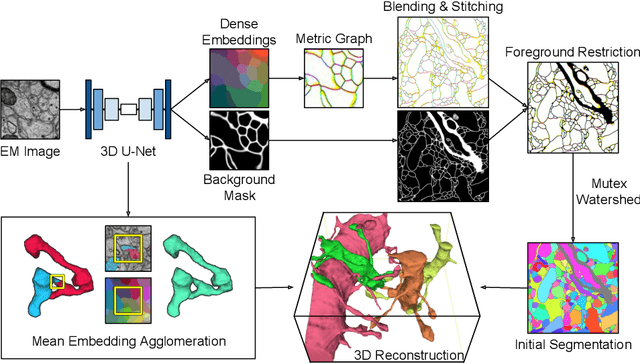
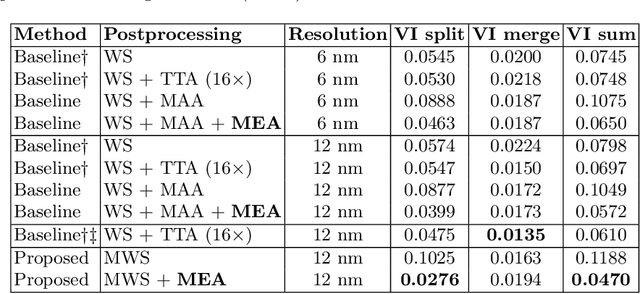
We show dense voxel embeddings learned via deep metric learning can be employed to produce a highly accurate segmentation of neurons from 3D electron microscopy images. A metric graph on an arbitrary set of short and long-range edges can be constructed from the dense embeddings generated by a convolutional network. Partitioning the metric graph with long-range affinities as repulsive constraints can produce an initial segmentation with high precision, with substantial improvements on very thin objects. The convolutional embedding net is reused without any modification to agglomerate the systematic splits caused by complex "self-touching"' objects. Our proposed method achieves state-of-the-art accuracy on the challenging problem of 3D neuron reconstruction from the brain images acquired by serial section electron microscopy. Our alternative, object-centered representation could be more generally useful for other computational tasks in automated neural circuit reconstruction.

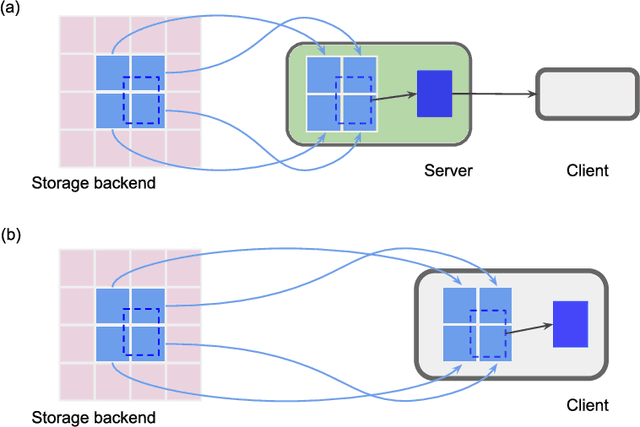
Chunkflow: Distributed Hybrid Cloud Processing of Large 3D Images by Convolutional Nets

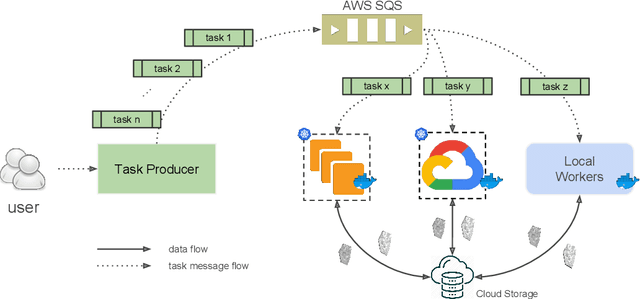
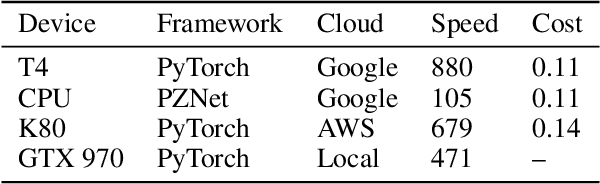
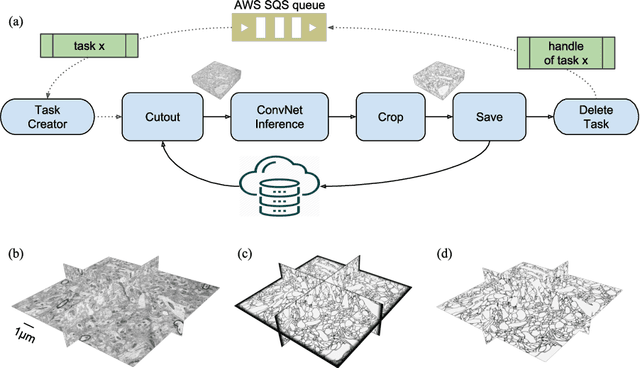
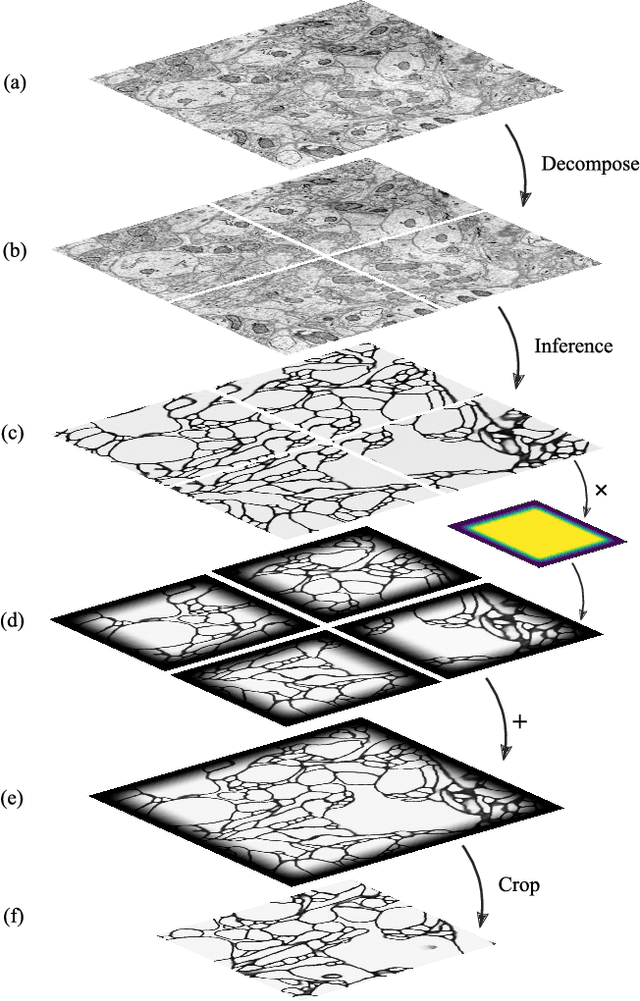
It is now common to process volumetric biomedical images using 3D Convolutional Networks (ConvNets). This can be challenging for the teravoxel and even petavoxel images that are being acquired today by light or electron microscopy. Here we introduce chunkflow, a software framework for distributing ConvNet processing over local and cloud GPUs and CPUs. The image volume is divided into overlapping chunks, each chunk is processed by a ConvNet, and the results are blended together to yield the output image. The frontend submits ConvNet tasks to a cloud queue. The tasks are executed by local and cloud GPUs and CPUs. Thanks to the fault-tolerant architecture of Chunkflow, cost can be greatly reduced by utilizing cheap unstable cloud instances. Chunkflow currently supports PyTorch for GPUs and PZnet for CPUs. To illustrate its usage, a large 3D brain image from serial section electron microscopy was processed by a 3D ConvNet with a U-Net style architecture. Chunkflow provides some chunk operations for general use, and the operations can be composed flexibly in a command line interface.

Convolutional nets for reconstructing neural circuits from brain images acquired by serial section electron microscopy

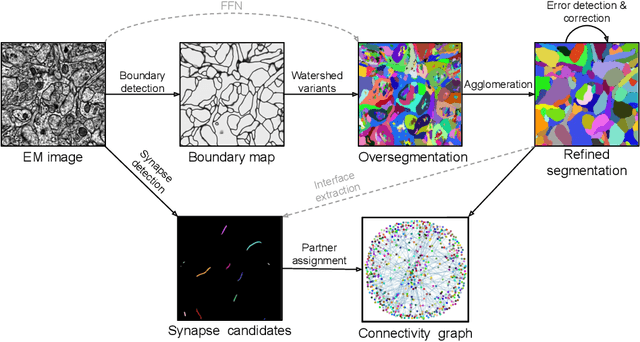
Neural circuits can be reconstructed from brain images acquired by serial section electron microscopy. Image analysis has been performed by manual labor for half a century, and efforts at automation date back almost as far. Convolutional nets were first applied to neuronal boundary detection a dozen years ago, and have now achieved impressive accuracy on clean images. Robust handling of image defects is a major outstanding challenge. Convolutional nets are also being employed for other tasks in neural circuit reconstruction: finding synapses and identifying synaptic partners, extending or pruning neuronal reconstructions, and aligning serial section images to create a 3D image stack. Computational systems are being engineered to handle petavoxel images of cubic millimeter brain volumes.

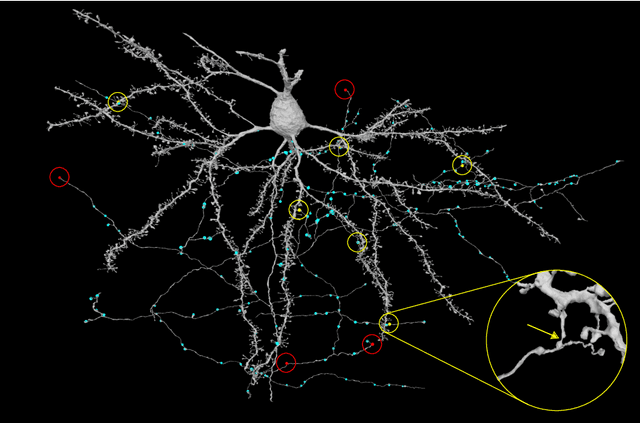
Synaptic Partner Assignment Using Attentional Voxel Association Networks

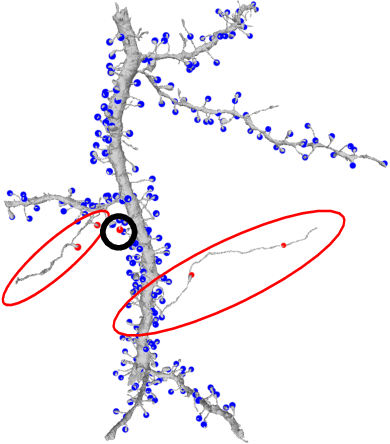
Connectomics aims to recover a complete set of synaptic connections within a dataset imaged by electron microscopy. Most systems for locating synapses use voxelwise classifier models, and train these classifiers to reproduce binary masks of synaptic clefts. However, only recent work has included a way to identify the synaptic partners that communicate at synaptic cleft segments. Here, we present a novel method for associating synaptic cleft segments with their synaptic partners using a convolutional network trained to associate the mask of a cleft with the voxels of its synaptic partners. The network takes the local image context and a mask of a single cleft segment as input. It is trained to produce two volumes of output: one which labels the voxels of the presynaptic partner within the input image, and another similar volume for the postsynaptic partner. The cleft mask acts as an attentional gating signal for the network, in that two clefts with the same local image context often have different partners. We find that an implementation of this approach performs well on a dataset of mouse somatosensory cortex, and evaluate it as part of a combined system to predict both clefts and connections.

Pixels to Plans: Learning Non-Prehensile Manipulation by Imitating a Planner

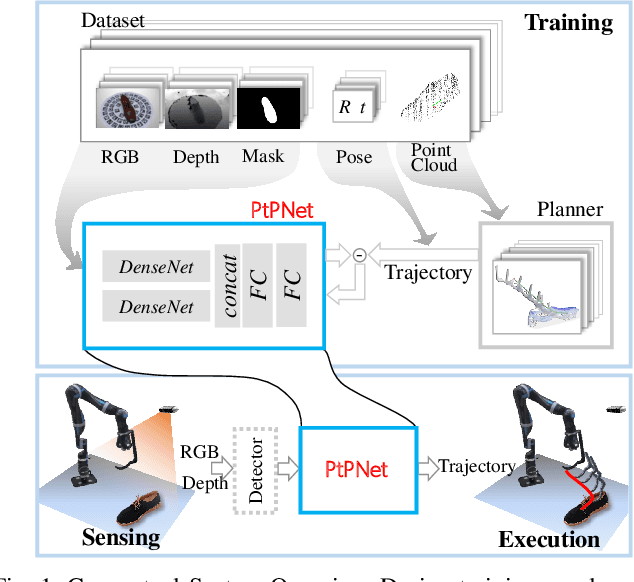
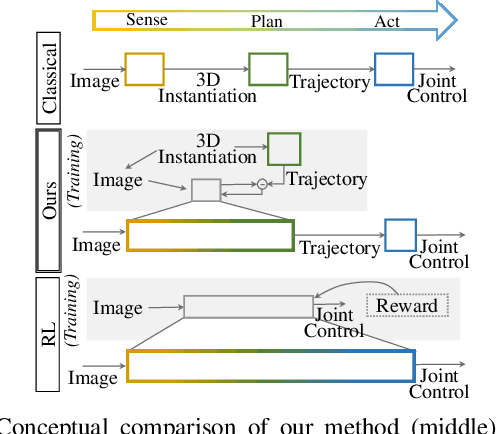
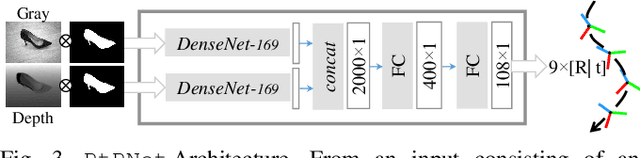
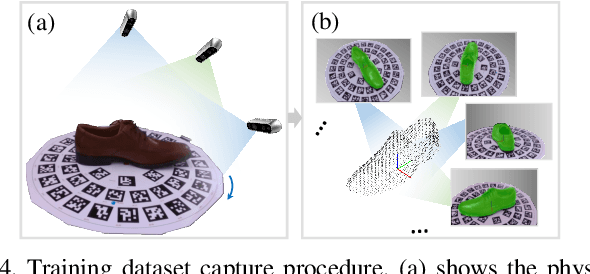
We present a novel method enabling robots to quickly learn to manipulate objects by leveraging a motion planner to generate "expert" training trajectories from a small amount of human-labeled data. In contrast to the traditional sense-plan-act cycle, we propose a deep learning architecture and training regimen called PtPNet that can estimate effective end-effector trajectories for manipulation directly from a single RGB-D image of an object. Additionally, we present a data collection and augmentation pipeline that enables the automatic generation of large numbers (millions) of training image and trajectory examples with almost no human labeling effort. We demonstrate our approach in a non-prehensile tool-based manipulation task, specifically picking up shoes with a hook. In hardware experiments, PtPNet generates motion plans (open-loop trajectories) that reliably (89% success over 189 trials) pick up four very different shoes from a range of positions and orientations, and reliably picks up a shoe it has never seen before. Compared with a traditional sense-plan-act paradigm, our system has the advantages of operating on sparse information (single RGB-D frame), producing high-quality trajectories much faster than the "expert" planner (300ms versus several seconds), and generalizing effectively to previously unseen shoes.