GPT-4o System Card

GPT-4o is an autoregressive omni model that accepts as input any combination of text, audio, image, and video, and generates any combination of text, audio, and image outputs. It's trained end-to-end across text, vision, and audio, meaning all inputs and outputs are processed by the same neural network. GPT-4o can respond to audio inputs in as little as 232 milliseconds, with an average of 320 milliseconds, which is similar to human response time in conversation. It matches GPT-4 Turbo performance on text in English and code, with significant improvement on text in non-English languages, while also being much faster and 50\% cheaper in the API. GPT-4o is especially better at vision and audio understanding compared to existing models. In line with our commitment to building AI safely and consistent with our voluntary commitments to the White House, we are sharing the GPT-4o System Card, which includes our Preparedness Framework evaluations. In this System Card, we provide a detailed look at GPT-4o's capabilities, limitations, and safety evaluations across multiple categories, focusing on speech-to-speech while also evaluating text and image capabilities, and measures we've implemented to ensure the model is safe and aligned. We also include third-party assessments on dangerous capabilities, as well as discussion of potential societal impacts of GPT-4o's text and vision capabilities.

DDGM: Solving inverse problems by Diffusive Denoising of Gradient-based Minimization

Inverse problems generally require a regularizer or prior for a good solution. A recent trend is to train a convolutional net to denoise images, and use this net as a prior when solving the inverse problem. Several proposals depend on a singular value decomposition of the forward operator, and several others backpropagate through the denoising net at runtime. Here we propose a simpler approach that combines the traditional gradient-based minimization of reconstruction error with denoising. Noise is also added at each step, so the iterative dynamics resembles a Langevin or diffusion process. Both the level of added noise and the size of the denoising step decay exponentially with time. We apply our method to the problem of tomographic reconstruction from electron micrographs acquired at multiple tilt angles. With empirical studies using simulated tilt views, we find parameter settings for our method that produce good results. We show that high accuracy can be achieved with as few as 50 denoising steps. We also compare with DDRM and DPS, more complex diffusion methods of the kinds mentioned above. These methods are less accurate (as measured by MSE and SSIM) for our tomography problem, even after the generation hyperparameters are optimized. Finally we extend our method to reconstruction of arbitrary-sized images and show results on 128 $\times$ 1568 pixel images

Stretched sinograms for limited-angle tomographic reconstruction with neural networks

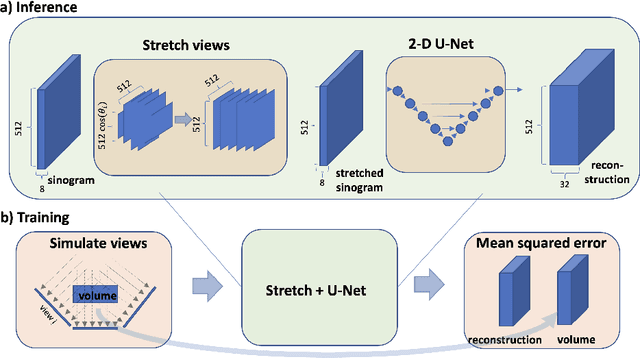
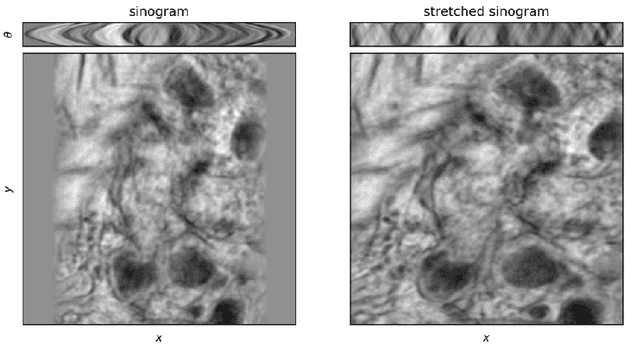
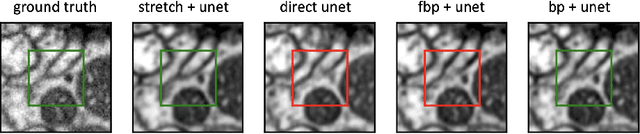
We present a direct method for limited angle tomographic reconstruction using convolutional networks. The key to our method is to first stretch every tilt view in the direction perpendicular to the tilt axis by the secant of the tilt angle. These stretched views are then fed into a 2-D U-Net which directly outputs the 3-D reconstruction. We train our networks by minimizing the mean squared error between the network's generated reconstruction and a ground truth 3-D volume. To demonstrate and evaluate our method, we synthesize tilt views from a 3-D image of fly brain tissue acquired with Focused Ion Beam Scanning Electron Microscopy. We compare our method to using a U-Net to directly reconstruct the unstretched tilt views and show that this simple stretching procedure leads to significantly better reconstructions. We also compare to using a network to clean up reconstructions generated by backprojection and filtered backprojection, and find that this simple stretching procedure also gives lower mean squared error on previously unseen images.

Stacked unsupervised learning with a network architecture found by supervised meta-learning

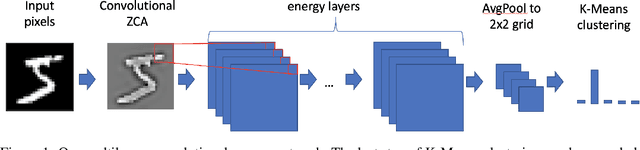
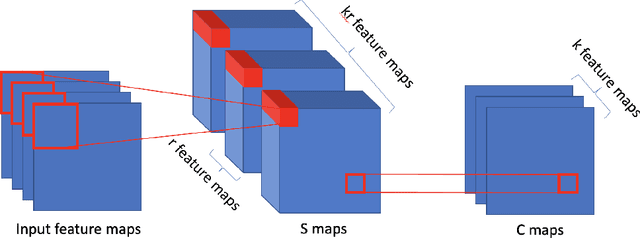
Stacked unsupervised learning (SUL) seems more biologically plausible than backpropagation, because learning is local to each layer. But SUL has fallen far short of backpropagation in practical applications, undermining the idea that SUL can explain how brains learn. Here we show an SUL algorithm that can perform completely unsupervised clustering of MNIST digits with comparable accuracy relative to unsupervised algorithms based on backpropagation. Our algorithm is exceeded only by self-supervised methods requiring training data augmentation by geometric distortions. The only prior knowledge in our unsupervised algorithm is implicit in the network architecture. Multiple convolutional "energy layers" contain a sum-of-squares nonlinearity, inspired by "energy models" of primary visual cortex. Convolutional kernels are learned with a fast minibatch implementation of the K-Subspaces algorithm. High accuracy requires preprocessing with an initial whitening layer, representations that are less sparse during inference than learning, and rescaling for gain control. The hyperparameters of the network architecture are found by supervised meta-learning, which optimizes unsupervised clustering accuracy. We regard such dependence of unsupervised learning on prior knowledge implicit in network architecture as biologically plausible, and analogous to the dependence of brain architecture on evolutionary history.

Kernel similarity matching with Hebbian neural networks

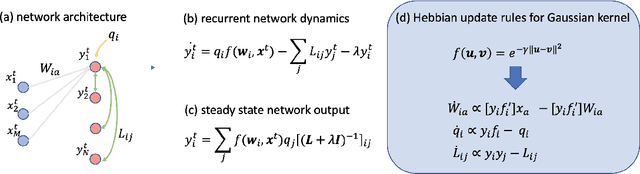
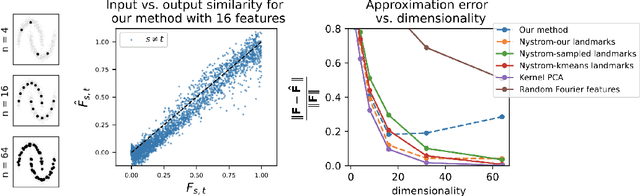
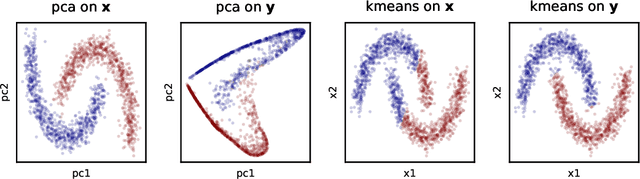
Recent works have derived neural networks with online correlation-based learning rules to perform \textit{kernel similarity matching}. These works applied existing linear similarity matching algorithms to nonlinear features generated with random Fourier methods. In this paper attempt to perform kernel similarity matching by directly learning the nonlinear features. Our algorithm proceeds by deriving and then minimizing an upper bound for the sum of squared errors between output and input kernel similarities. The construction of our upper bound leads to online correlation-based learning rules which can be implemented with a 1 layer recurrent neural network. In addition to generating high-dimensional linearly separable representations, we show that our upper bound naturally yields representations which are sparse and selective for specific input patterns. We compare the approximation quality of our method to neural random Fourier method and variants of the popular but non-biological "Nystr{\"o}m" method for approximating the kernel matrix. Our method appears to be comparable or better than randomly sampled Nystr{\"o}m methods when the outputs are relatively low dimensional (although still potentially higher dimensional than the inputs) but less faithful when the outputs are very high dimensional.

Sensitivity of sparse codes to image distortions

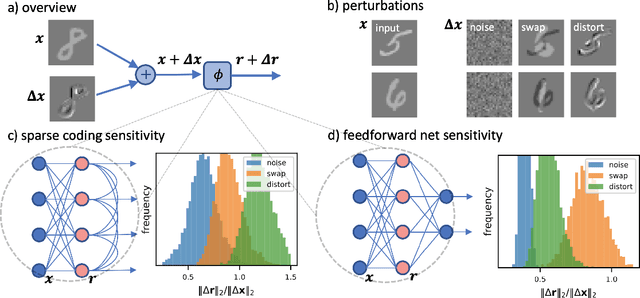
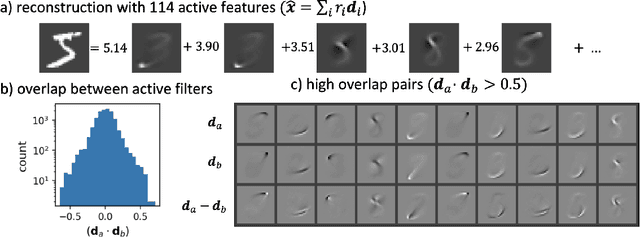
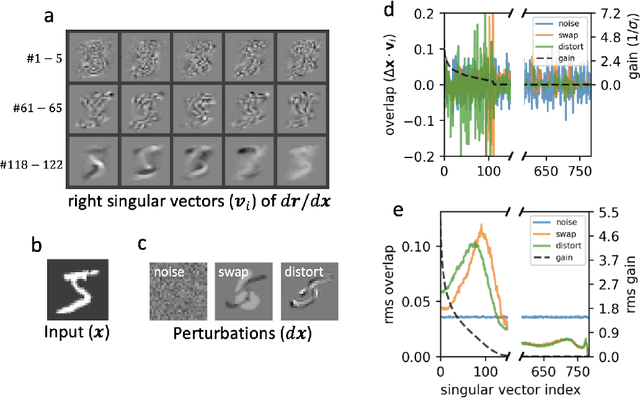
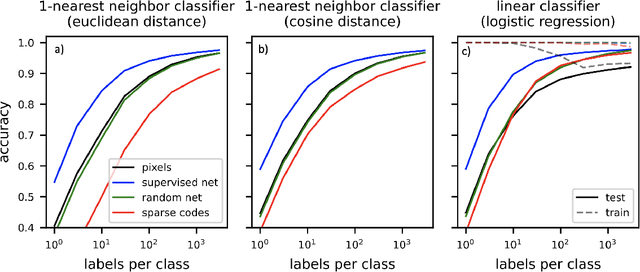
Sparse coding has been proposed as a theory of visual cortex and as an unsupervised algorithm for learning representations. We show empirically with the MNIST dataset that sparse codes can be very sensitive to image distortions, a behavior that may hinder invariant object recognition. A locally linear analysis suggests that the sensitivity is due to the existence of linear combinations of active dictionary elements with high cancellation. A nearest neighbor classifier is shown to perform worse on sparse codes than original images. For a linear classifier with a sufficiently large number of labeled examples, sparse codes are shown to yield higher accuracy than original images, but no higher than a representation computed by a random feedforward net. Sensitivity to distortions seems to be a basic property of sparse codes, and one should be aware of this property when applying sparse codes to invariant object recognition.

Learning Dense Voxel Embeddings for 3D Neuron Reconstruction

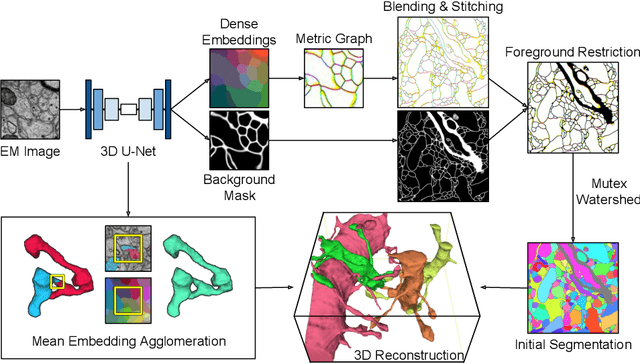
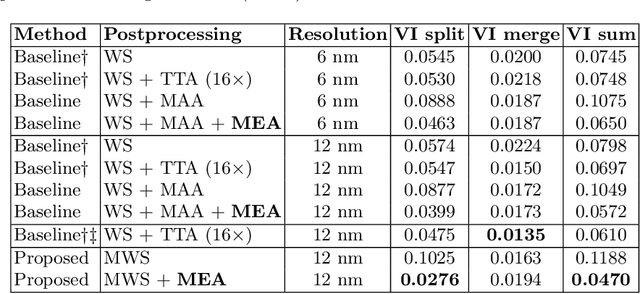
We show dense voxel embeddings learned via deep metric learning can be employed to produce a highly accurate segmentation of neurons from 3D electron microscopy images. A metric graph on an arbitrary set of short and long-range edges can be constructed from the dense embeddings generated by a convolutional network. Partitioning the metric graph with long-range affinities as repulsive constraints can produce an initial segmentation with high precision, with substantial improvements on very thin objects. The convolutional embedding net is reused without any modification to agglomerate the systematic splits caused by complex "self-touching"' objects. Our proposed method achieves state-of-the-art accuracy on the challenging problem of 3D neuron reconstruction from the brain images acquired by serial section electron microscopy. Our alternative, object-centered representation could be more generally useful for other computational tasks in automated neural circuit reconstruction.

Variance-Preserving Initialization Schemes Improve Deep Network Training: But Which Variance is Preserved?

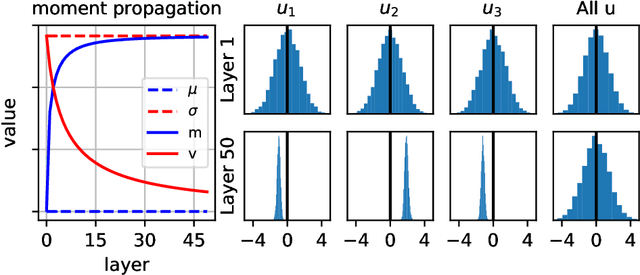
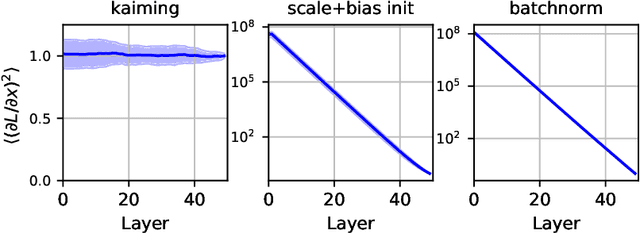
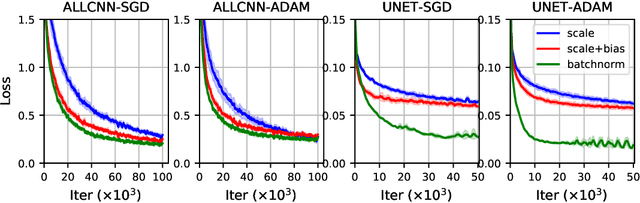
Before training a neural net, a classic rule of thumb is to randomly initialize the weights so that the variance of the preactivation is preserved across all layers. This is traditionally interpreted using the total variance due to randomness in both networks (weights) and samples. Alternatively, one can interpret the rule of thumb as preservation of the \emph{sample} mean and variance for a fixed network, i.e., preactivation statistics computed over the random sample of training samples. The two interpretations differ little for a shallow net, but the difference is shown to be large for a deep ReLU net by decomposing the total variance into the network-averaged sum of the sample variance and square of the sample mean. We demonstrate that the latter term dominates in the later layers through an analytical calculation in the limit of infinite network width, and numerical simulations for finite width. Our experimental results from training neural nets support the idea that preserving sample statistics can be better than preserving total variance. We discuss the implications for the alternative rule of thumb that a network should be initialized to be at the "edge of chaos."

Learning Metric Graphs for Neuron Segmentation In Electron Microscopy Images

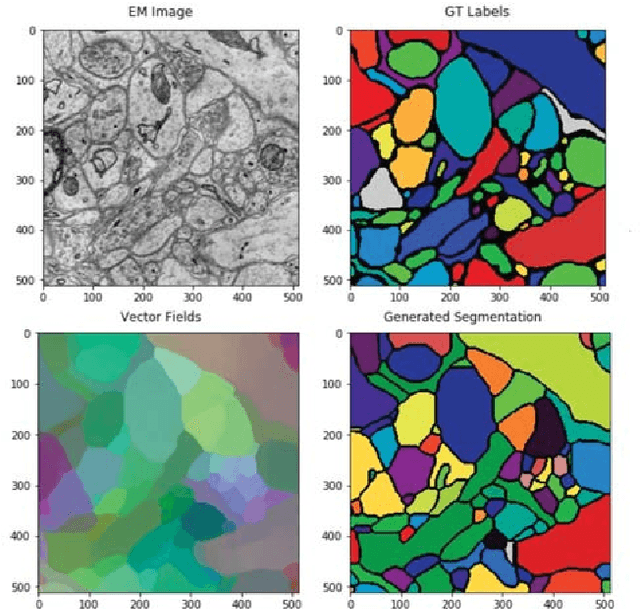
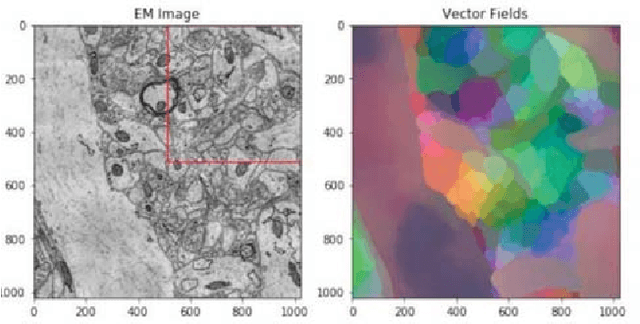
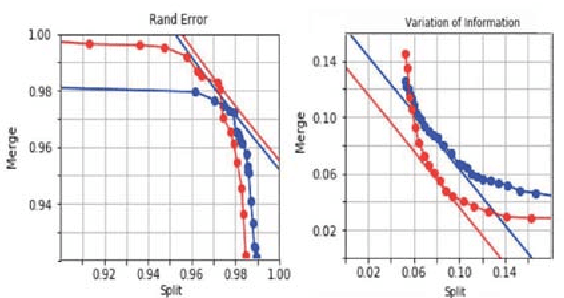
In the deep metric learning approach to image segmentation, a convolutional net densely generates feature vectors at the pixels of an image. Pairs of feature vectors are trained to be similar or different, depending on whether the corresponding pixels belong to same or different ground truth segments. To segment a new image, the feature vectors are computed and clustered. Both empirically and theoretically, it is unclear whether or when deep metric learning is superior to the more conventional approach of directly predicting an affinity graph with a convolutional net. We compare the two approaches using brain images from serial section electron microscopy images, which constitute an especially challenging example of instance segmentation. We first show that seed-based postprocessing of the feature vectors, as originally proposed, produces inferior accuracy because it is difficult for the convolutional net to predict feature vectors that remain uniform across large objects. Then we consider postprocessing by thresholding a nearest neighbor graph followed by connected components. In this case, segmentations from a "metric graph" turn out to be competitive or even superior to segmentations from a directly predicted affinity graph. To explain these findings theoretically, we invoke the property that the metric function satisfies the triangle inequality. Then we show with an example where this constraint suppresses noise, causing connected components to more robustly segment a metric graph than an unconstrained affinity graph.