Variance-Preserving Initialization Schemes Improve Deep Network Training: But Which Variance is Preserved?

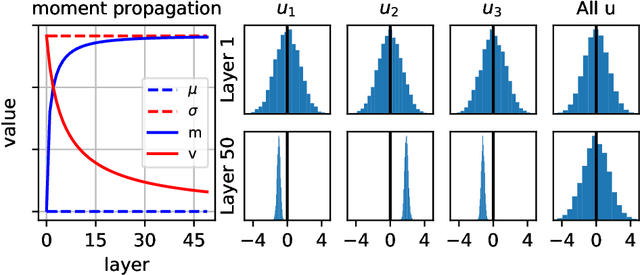
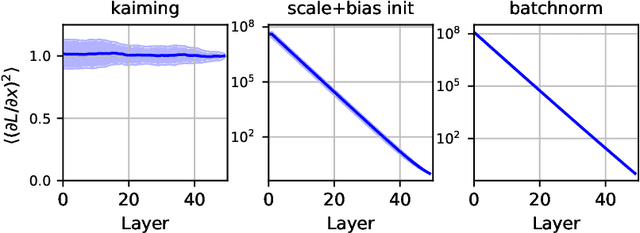
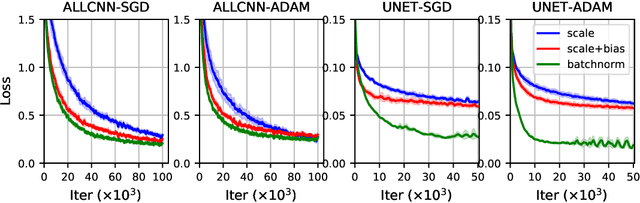
Before training a neural net, a classic rule of thumb is to randomly initialize the weights so that the variance of the preactivation is preserved across all layers. This is traditionally interpreted using the total variance due to randomness in both networks (weights) and samples. Alternatively, one can interpret the rule of thumb as preservation of the \emph{sample} mean and variance for a fixed network, i.e., preactivation statistics computed over the random sample of training samples. The two interpretations differ little for a shallow net, but the difference is shown to be large for a deep ReLU net by decomposing the total variance into the network-averaged sum of the sample variance and square of the sample mean. We demonstrate that the latter term dominates in the later layers through an analytical calculation in the limit of infinite network width, and numerical simulations for finite width. Our experimental results from training neural nets support the idea that preserving sample statistics can be better than preserving total variance. We discuss the implications for the alternative rule of thumb that a network should be initialized to be at the "edge of chaos."