Stacked unsupervised learning with a network architecture found by supervised meta-learning
Paper and Code
Jun 06, 2022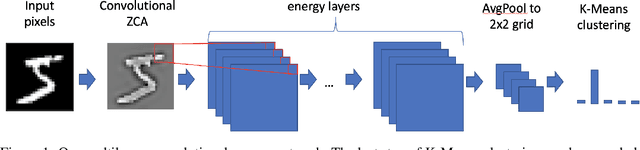

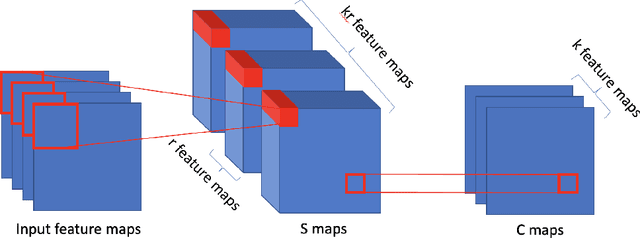

Stacked unsupervised learning (SUL) seems more biologically plausible than backpropagation, because learning is local to each layer. But SUL has fallen far short of backpropagation in practical applications, undermining the idea that SUL can explain how brains learn. Here we show an SUL algorithm that can perform completely unsupervised clustering of MNIST digits with comparable accuracy relative to unsupervised algorithms based on backpropagation. Our algorithm is exceeded only by self-supervised methods requiring training data augmentation by geometric distortions. The only prior knowledge in our unsupervised algorithm is implicit in the network architecture. Multiple convolutional "energy layers" contain a sum-of-squares nonlinearity, inspired by "energy models" of primary visual cortex. Convolutional kernels are learned with a fast minibatch implementation of the K-Subspaces algorithm. High accuracy requires preprocessing with an initial whitening layer, representations that are less sparse during inference than learning, and rescaling for gain control. The hyperparameters of the network architecture are found by supervised meta-learning, which optimizes unsupervised clustering accuracy. We regard such dependence of unsupervised learning on prior knowledge implicit in network architecture as biologically plausible, and analogous to the dependence of brain architecture on evolutionary history.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge