DPR: Diffusion Preference-based Reward for Offline Reinforcement Learning

Offline preference-based reinforcement learning (PbRL) mitigates the need for reward definition, aligning with human preferences via preference-driven reward feedback without interacting with the environment. However, the effectiveness of preference-driven reward functions depends on the modeling ability of the learning model, which current MLP-based and Transformer-based methods may fail to adequately provide. To alleviate the failure of the reward function caused by insufficient modeling, we propose a novel preference-based reward acquisition method: Diffusion Preference-based Reward (DPR). Unlike previous methods using Bradley-Terry models for trajectory preferences, we use diffusion models to directly model preference distributions for state-action pairs, allowing rewards to be discriminatively obtained from these distributions. In addition, considering the particularity of preference data that only know the internal relationships of paired trajectories, we further propose Conditional Diffusion Preference-based Reward (C-DPR), which leverages relative preference information to enhance the construction of the diffusion model. We apply the above methods to existing offline reinforcement learning algorithms and a series of experiment results demonstrate that the diffusion-based reward acquisition approach outperforms previous MLP-based and Transformer-based methods.

Sharper Concentration Inequalities for Multi-Graph Dependent Variables

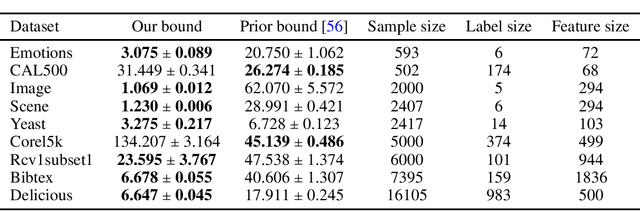
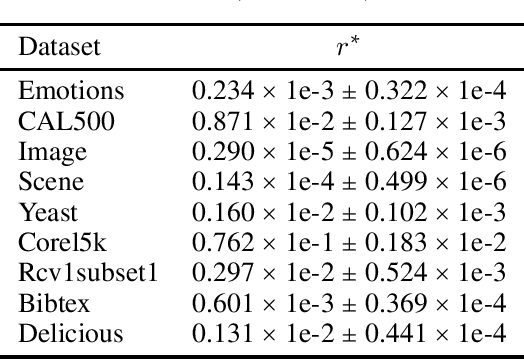
In multi-task learning (MTL) with each task involving graph-dependent data, generalization results of existing theoretical analyses yield a sub-optimal risk bound of $O(\frac{1}{\sqrt{n}})$, where $n$ is the number of training samples.This is attributed to the lack of a foundational sharper concentration inequality for multi-graph dependent random variables. To fill this gap, this paper proposes a new corresponding Bennett inequality, enabling the derivation of a sharper risk bound of $O(\frac{\log n}{n})$. Specifically, building on the proposed Bennett inequality, we propose a new corresponding Talagrand inequality for the empirical process and further develop an analytical framework of the local Rademacher complexity to enhance theoretical generalization analyses in MTL with multi-graph dependent data. Finally, we apply the theoretical advancements to applications such as Macro-AUC Optimization, demonstrating the superiority of our theoretical results over previous work, which is also corroborated by experimental results.

A Theory for Conditional Generative Modeling on Multiple Data Sources

The success of large generative models has driven a paradigm shift, leveraging massive multi-source data to enhance model capabilities. However, the interaction among these sources remains theoretically underexplored. This paper takes the first step toward a rigorous analysis of multi-source training in conditional generative modeling, where each condition represents a distinct data source. Specifically, we establish a general distribution estimation error bound in average total variation distance for conditional maximum likelihood estimation based on the bracketing number. Our result shows that when source distributions share certain similarities and the model is expressive enough, multi-source training guarantees a sharper bound than single-source training. We further instantiate the general theory on conditional Gaussian estimation and deep generative models including autoregressive and flexible energy-based models, by characterizing their bracketing numbers. The results highlight that the number of sources and similarity among source distributions improve the advantage of multi-source training. Simulations and real-world experiments validate our theory. Code is available at: \url{https://github.com/ML-GSAI/Multi-Source-GM}.

Towards Macro-AUC oriented Imbalanced Multi-Label Continual Learning

In Continual Learning (CL), while existing work primarily focuses on the multi-class classification task, there has been limited research on Multi-Label Learning (MLL). In practice, MLL datasets are often class-imbalanced, making it inherently challenging, a problem that is even more acute in CL. Due to its sensitivity to imbalance, Macro-AUC is an appropriate and widely used measure in MLL. However, there is no research to optimize Macro-AUC in MLCL specifically. To fill this gap, in this paper, we propose a new memory replay-based method to tackle the imbalance issue for Macro-AUC-oriented MLCL. Specifically, inspired by recent theory work, we propose a new Reweighted Label-Distribution-Aware Margin (RLDAM) loss. Furthermore, to be compatible with the RLDAM loss, a new memory-updating strategy named Weight Retain Updating (WRU) is proposed to maintain the numbers of positive and negative instances of the original dataset in memory. Theoretically, we provide superior generalization analyses of the RLDAM-based algorithm in terms of Macro-AUC, separately in batch MLL and MLCL settings. This is the first work to offer theoretical generalization analyses in MLCL to our knowledge. Finally, a series of experimental results illustrate the effectiveness of our method over several baselines. Our codes are available at https://github.com/ML-Group-SDU/Macro-AUC-CL.

IPL: Leveraging Multimodal Large Language Models for Intelligent Product Listing

Unlike professional Business-to-Consumer (B2C) e-commerce platforms (e.g., Amazon), Consumer-to-Consumer (C2C) platforms (e.g., Facebook marketplace) are mainly targeting individual sellers who usually lack sufficient experience in e-commerce. Individual sellers often struggle to compose proper descriptions for selling products. With the recent advancement of Multimodal Large Language Models (MLLMs), we attempt to integrate such state-of-the-art generative AI technologies into the product listing process. To this end, we develop IPL, an Intelligent Product Listing tool tailored to generate descriptions using various product attributes such as category, brand, color, condition, etc. IPL enables users to compose product descriptions by merely uploading photos of the selling product. More importantly, it can imitate the content style of our C2C platform Xianyu. This is achieved by employing domain-specific instruction tuning on MLLMs and adopting the multi-modal Retrieval-Augmented Generation (RAG) process. A comprehensive empirical evaluation demonstrates that the underlying model of IPL significantly outperforms the base model in domain-specific tasks while producing less hallucination. IPL has been successfully deployed in our production system, where 72% of users have their published product listings based on the generated content, and those product listings are shown to have a quality score 5.6% higher than those without AI assistance.

Learning to Race in Extreme Turning Scene with Active Exploration and Gaussian Process Regression-based MPC

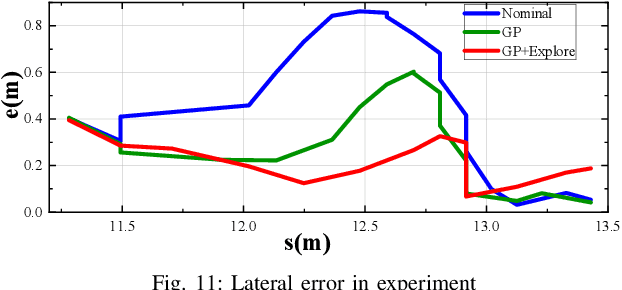
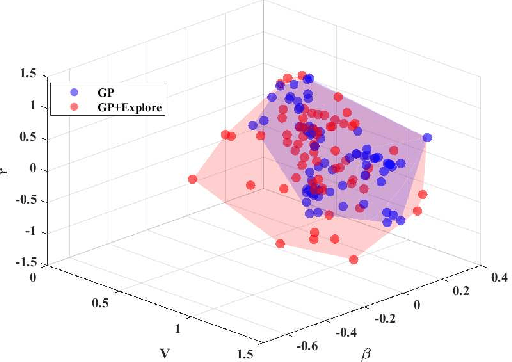
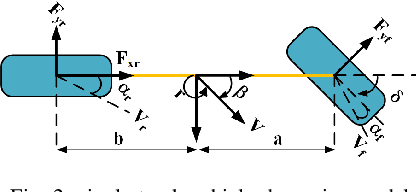
Extreme cornering in racing often induces large side-slip angles, presenting a formidable challenge in vehicle control. To tackle this issue, this paper introduces an Active Exploration with Double GPR (AEDGPR) system. The system initiates by planning a minimum-time trajectory with a Gaussian Process Regression(GPR) compensated model. The planning results show that in the cornering section, the yaw angular velocity and side-slip angle are in opposite directions, indicating that the vehicle is drifting. In response, we develop a drift controller based on Model Predictive Control (MPC) and incorporate Gaussian Process Regression to correct discrepancies in the vehicle dynamics model. Moreover, the covariance from the GPR is employed to actively explore various cornering states, aiming to minimize trajectory tracking errors. The proposed algorithm is validated through simulations on the Simulink-Carsim platform and experiments using a 1/10 scale RC vehicle.

On Mesa-Optimization in Autoregressively Trained Transformers: Emergence and Capability

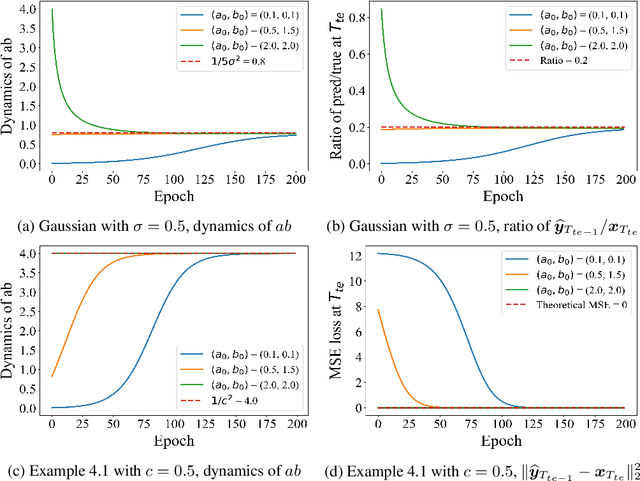
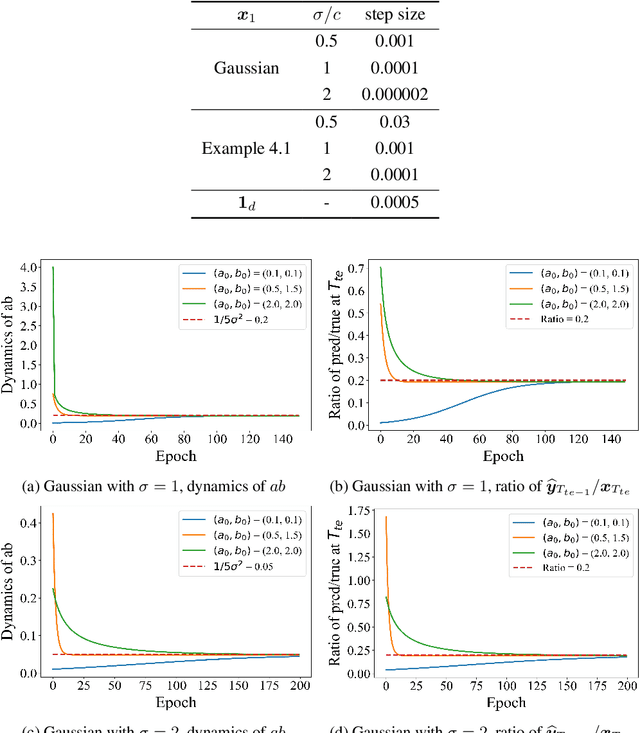
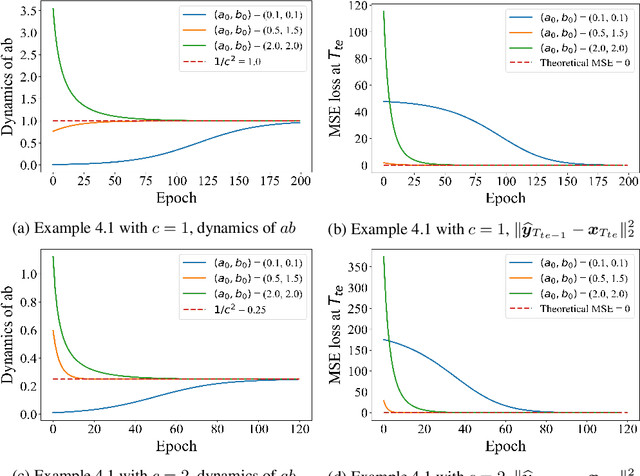
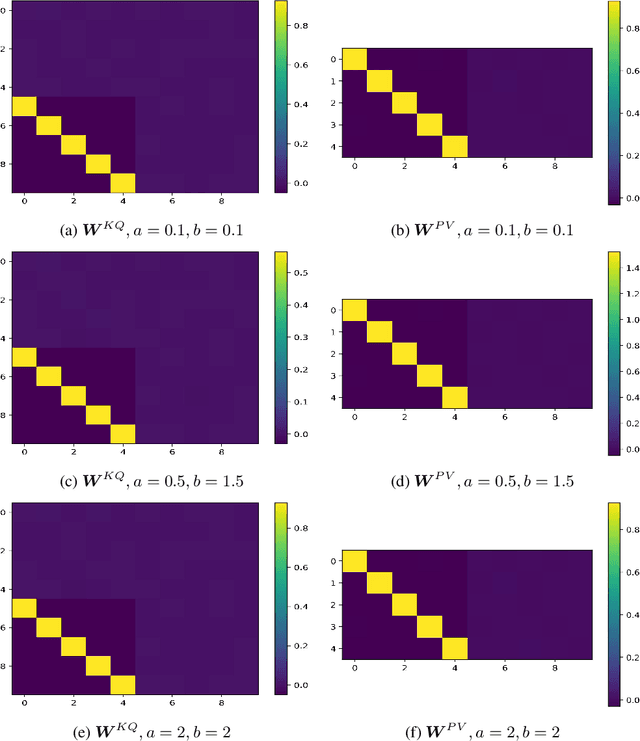
Autoregressively trained transformers have brought a profound revolution to the world, especially with their in-context learning (ICL) ability to address downstream tasks. Recently, several studies suggest that transformers learn a mesa-optimizer during autoregressive (AR) pretraining to implement ICL. Namely, the forward pass of the trained transformer is equivalent to optimizing an inner objective function in-context. However, whether the practical non-convex training dynamics will converge to the ideal mesa-optimizer is still unclear. Towards filling this gap, we investigate the non-convex dynamics of a one-layer linear causal self-attention model autoregressively trained by gradient flow, where the sequences are generated by an AR process $x_{t+1} = W x_t$. First, under a certain condition of data distribution, we prove that an autoregressively trained transformer learns $W$ by implementing one step of gradient descent to minimize an ordinary least squares (OLS) problem in-context. It then applies the learned $\widehat{W}$ for next-token prediction, thereby verifying the mesa-optimization hypothesis. Next, under the same data conditions, we explore the capability limitations of the obtained mesa-optimizer. We show that a stronger assumption related to the moments of data is the sufficient and necessary condition that the learned mesa-optimizer recovers the distribution. Besides, we conduct exploratory analyses beyond the first data condition and prove that generally, the trained transformer will not perform vanilla gradient descent for the OLS problem. Finally, our simulation results verify the theoretical results.

DiffAIL: Diffusion Adversarial Imitation Learning

Imitation learning aims to solve the problem of defining reward functions in real-world decision-making tasks. The current popular approach is the Adversarial Imitation Learning (AIL) framework, which matches expert state-action occupancy measures to obtain a surrogate reward for forward reinforcement learning. However, the traditional discriminator is a simple binary classifier and doesn't learn an accurate distribution, which may result in failing to identify expert-level state-action pairs induced by the policy interacting with the environment. To address this issue, we propose a method named diffusion adversarial imitation learning (DiffAIL), which introduces the diffusion model into the AIL framework. Specifically, DiffAIL models the state-action pairs as unconditional diffusion models and uses diffusion loss as part of the discriminator's learning objective, which enables the discriminator to capture better expert demonstrations and improve generalization. Experimentally, the results show that our method achieves state-of-the-art performance and significantly surpasses expert demonstration on two benchmark tasks, including the standard state-action setting and state-only settings. Our code can be available at the link https://github.com/ML-Group-SDU/DiffAIL.

Toward Understanding Generative Data Augmentation

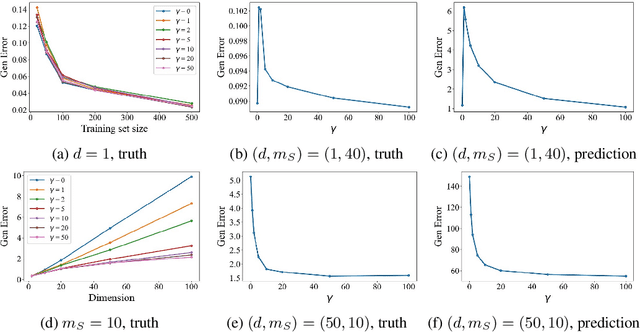
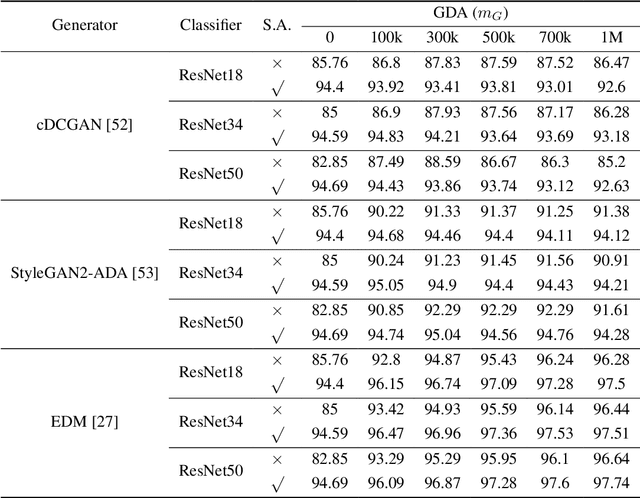
Generative data augmentation, which scales datasets by obtaining fake labeled examples from a trained conditional generative model, boosts classification performance in various learning tasks including (semi-)supervised learning, few-shot learning, and adversarially robust learning. However, little work has theoretically investigated the effect of generative data augmentation. To fill this gap, we establish a general stability bound in this not independently and identically distributed (non-i.i.d.) setting, where the learned distribution is dependent on the original train set and generally not the same as the true distribution. Our theoretical result includes the divergence between the learned distribution and the true distribution. It shows that generative data augmentation can enjoy a faster learning rate when the order of divergence term is $o(\max\left( \log(m)\beta_m, 1 / \sqrt{m})\right)$, where $m$ is the train set size and $\beta_m$ is the corresponding stability constant. We further specify the learning setup to the Gaussian mixture model and generative adversarial nets. We prove that in both cases, though generative data augmentation does not enjoy a faster learning rate, it can improve the learning guarantees at a constant level when the train set is small, which is significant when the awful overfitting occurs. Simulation results on the Gaussian mixture model and empirical results on generative adversarial nets support our theoretical conclusions. Our code is available at https://github.com/ML-GSAI/Understanding-GDA.

Towards Understanding Generalization of Macro-AUC in Multi-label Learning

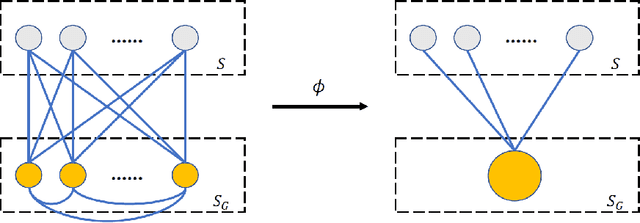
Macro-AUC is the arithmetic mean of the class-wise AUCs in multi-label learning and is commonly used in practice. However, its theoretical understanding is far lacking. Toward solving it, we characterize the generalization properties of various learning algorithms based on the corresponding surrogate losses w.r.t. Macro-AUC. We theoretically identify a critical factor of the dataset affecting the generalization bounds: \emph{the label-wise class imbalance}. Our results on the imbalance-aware error bounds show that the widely-used univariate loss-based algorithm is more sensitive to the label-wise class imbalance than the proposed pairwise and reweighted loss-based ones, which probably implies its worse performance. Moreover, empirical results on various datasets corroborate our theory findings. To establish it, technically, we propose a new (and more general) McDiarmid-type concentration inequality, which may be of independent interest.