A Theory for Conditional Generative Modeling on Multiple Data Sources

The success of large generative models has driven a paradigm shift, leveraging massive multi-source data to enhance model capabilities. However, the interaction among these sources remains theoretically underexplored. This paper takes the first step toward a rigorous analysis of multi-source training in conditional generative modeling, where each condition represents a distinct data source. Specifically, we establish a general distribution estimation error bound in average total variation distance for conditional maximum likelihood estimation based on the bracketing number. Our result shows that when source distributions share certain similarities and the model is expressive enough, multi-source training guarantees a sharper bound than single-source training. We further instantiate the general theory on conditional Gaussian estimation and deep generative models including autoregressive and flexible energy-based models, by characterizing their bracketing numbers. The results highlight that the number of sources and similarity among source distributions improve the advantage of multi-source training. Simulations and real-world experiments validate our theory. Code is available at: \url{https://github.com/ML-GSAI/Multi-Source-GM}.

On Mesa-Optimization in Autoregressively Trained Transformers: Emergence and Capability

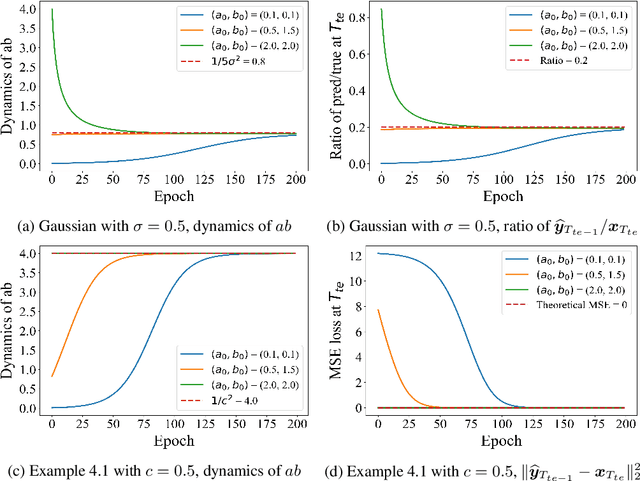
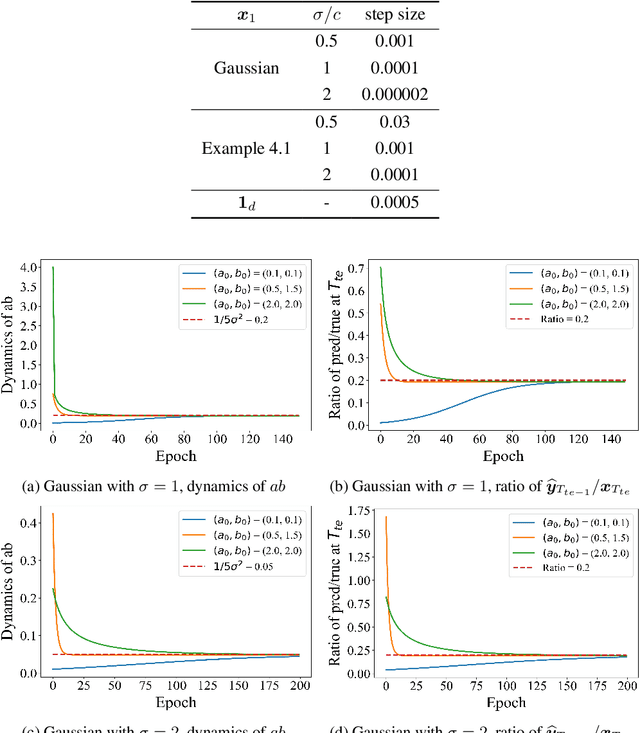
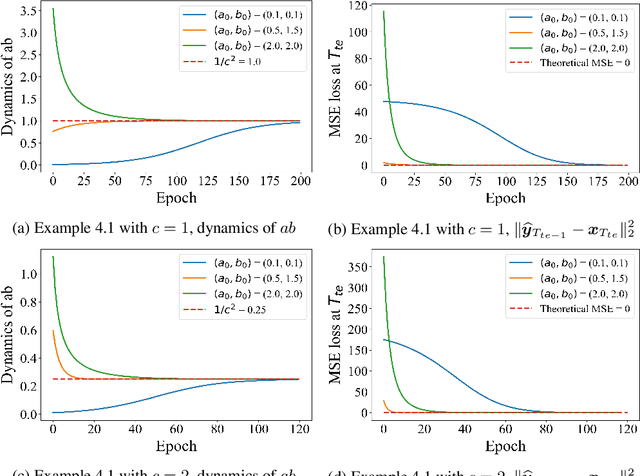
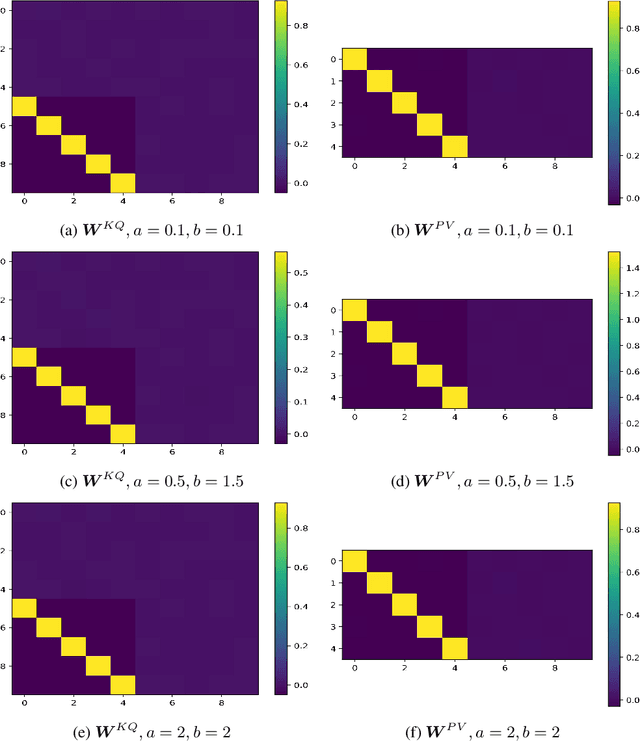
Autoregressively trained transformers have brought a profound revolution to the world, especially with their in-context learning (ICL) ability to address downstream tasks. Recently, several studies suggest that transformers learn a mesa-optimizer during autoregressive (AR) pretraining to implement ICL. Namely, the forward pass of the trained transformer is equivalent to optimizing an inner objective function in-context. However, whether the practical non-convex training dynamics will converge to the ideal mesa-optimizer is still unclear. Towards filling this gap, we investigate the non-convex dynamics of a one-layer linear causal self-attention model autoregressively trained by gradient flow, where the sequences are generated by an AR process $x_{t+1} = W x_t$. First, under a certain condition of data distribution, we prove that an autoregressively trained transformer learns $W$ by implementing one step of gradient descent to minimize an ordinary least squares (OLS) problem in-context. It then applies the learned $\widehat{W}$ for next-token prediction, thereby verifying the mesa-optimization hypothesis. Next, under the same data conditions, we explore the capability limitations of the obtained mesa-optimizer. We show that a stronger assumption related to the moments of data is the sufficient and necessary condition that the learned mesa-optimizer recovers the distribution. Besides, we conduct exploratory analyses beyond the first data condition and prove that generally, the trained transformer will not perform vanilla gradient descent for the OLS problem. Finally, our simulation results verify the theoretical results.

The Blessing of Randomness: SDE Beats ODE in General Diffusion-based Image Editing

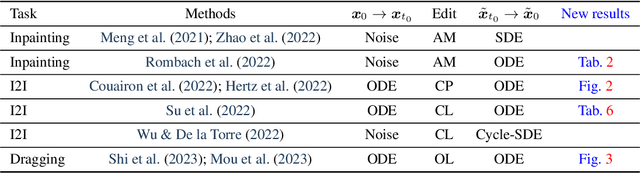
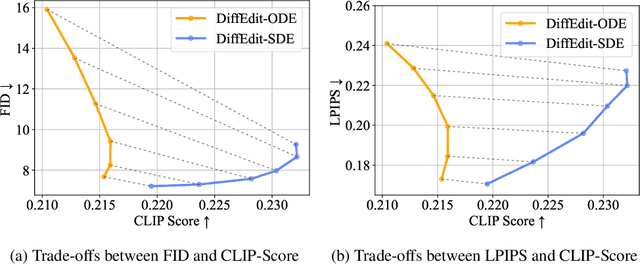
We present a unified probabilistic formulation for diffusion-based image editing, where a latent variable is edited in a task-specific manner and generally deviates from the corresponding marginal distribution induced by the original stochastic or ordinary differential equation (SDE or ODE). Instead, it defines a corresponding SDE or ODE for editing. In the formulation, we prove that the Kullback-Leibler divergence between the marginal distributions of the two SDEs gradually decreases while that for the ODEs remains as the time approaches zero, which shows the promise of SDE in image editing. Inspired by it, we provide the SDE counterparts for widely used ODE baselines in various tasks including inpainting and image-to-image translation, where SDE shows a consistent and substantial improvement. Moreover, we propose SDE-Drag -- a simple yet effective method built upon the SDE formulation for point-based content dragging. We build a challenging benchmark (termed DragBench) with open-set natural, art, and AI-generated images for evaluation. A user study on DragBench indicates that SDE-Drag significantly outperforms our ODE baseline, existing diffusion-based methods, and the renowned DragGAN. Our results demonstrate the superiority and versatility of SDE in image editing and push the boundary of diffusion-based editing methods.

Toward Understanding Generative Data Augmentation

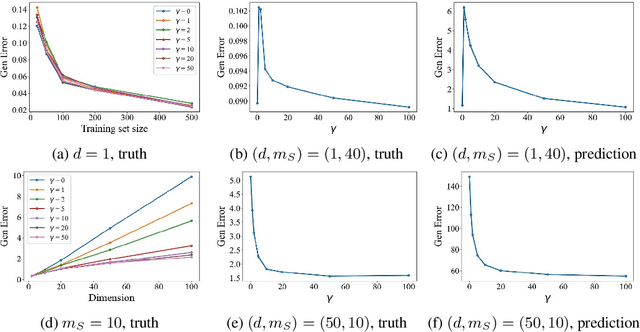
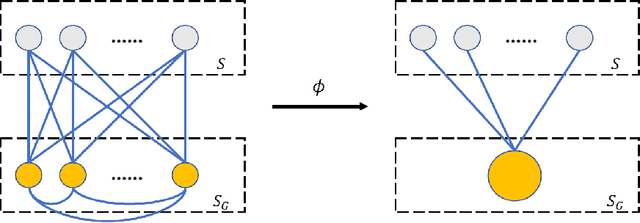
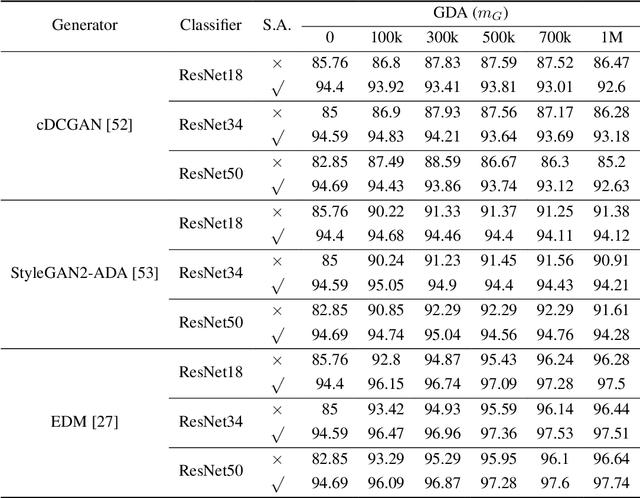
Generative data augmentation, which scales datasets by obtaining fake labeled examples from a trained conditional generative model, boosts classification performance in various learning tasks including (semi-)supervised learning, few-shot learning, and adversarially robust learning. However, little work has theoretically investigated the effect of generative data augmentation. To fill this gap, we establish a general stability bound in this not independently and identically distributed (non-i.i.d.) setting, where the learned distribution is dependent on the original train set and generally not the same as the true distribution. Our theoretical result includes the divergence between the learned distribution and the true distribution. It shows that generative data augmentation can enjoy a faster learning rate when the order of divergence term is $o(\max\left( \log(m)\beta_m, 1 / \sqrt{m})\right)$, where $m$ is the train set size and $\beta_m$ is the corresponding stability constant. We further specify the learning setup to the Gaussian mixture model and generative adversarial nets. We prove that in both cases, though generative data augmentation does not enjoy a faster learning rate, it can improve the learning guarantees at a constant level when the train set is small, which is significant when the awful overfitting occurs. Simulation results on the Gaussian mixture model and empirical results on generative adversarial nets support our theoretical conclusions. Our code is available at https://github.com/ML-GSAI/Understanding-GDA.

Revisiting Discriminative vs. Generative Classifiers: Theory and Implications

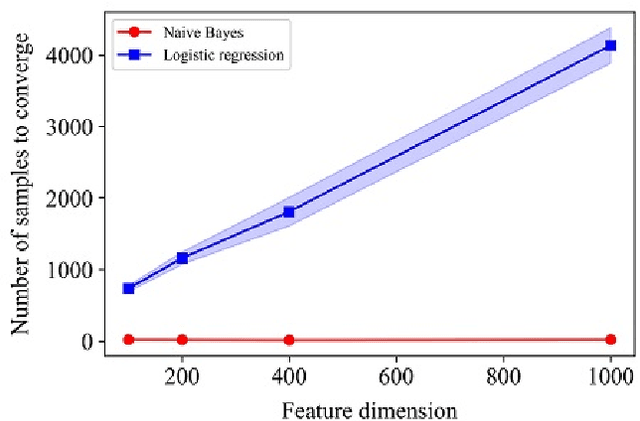
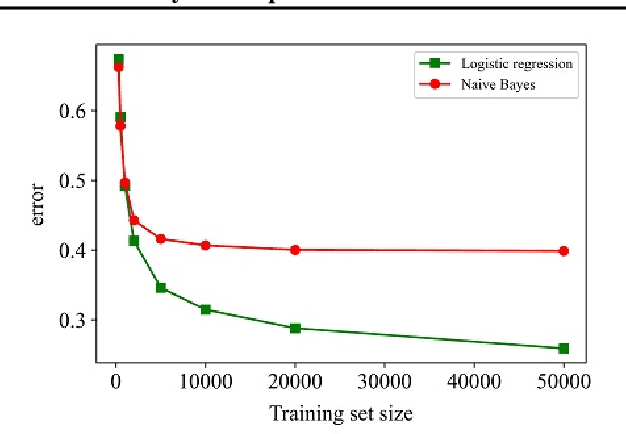
A large-scale deep model pre-trained on massive labeled or unlabeled data transfers well to downstream tasks. Linear evaluation freezes parameters in the pre-trained model and trains a linear classifier separately, which is efficient and attractive for transfer. However, little work has investigated the classifier in linear evaluation except for the default logistic regression. Inspired by the statistical efficiency of naive Bayes, the paper revisits the classical topic on discriminative vs. generative classifiers. Theoretically, the paper considers the surrogate loss instead of the zero-one loss in analyses and generalizes the classical results from binary cases to multiclass ones. We show that, under mild assumptions, multiclass naive Bayes requires $O(\log n)$ samples to approach its asymptotic error while the corresponding multiclass logistic regression requires $O(n)$ samples, where $n$ is the feature dimension. To establish it, we present a multiclass $\mathcal{H}$-consistency bound framework and an explicit bound for logistic loss, which are of independent interests. Simulation results on a mixture of Gaussian validate our theoretical findings. Experiments on various pre-trained deep vision models show that naive Bayes consistently converges faster as the number of data increases. Besides, naive Bayes shows promise in few-shot cases and we observe the ``two regimes'' phenomenon in pre-trained supervised models. Our code is available at https://github.com/ML-GSAI/Revisiting-Dis-vs-Gen-Classifiers.

AutoLC: Search Lightweight and Top-Performing Architecture for Remote Sensing Image Land-Cover Classification

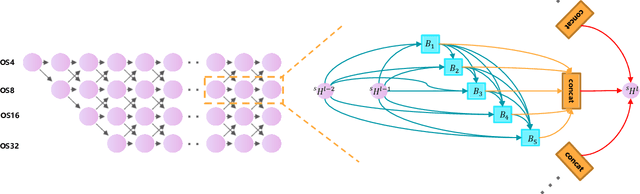
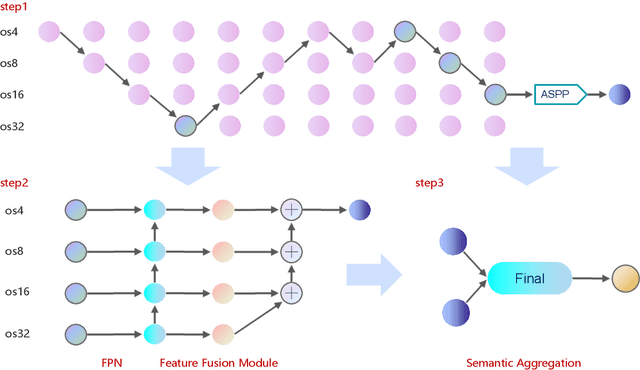
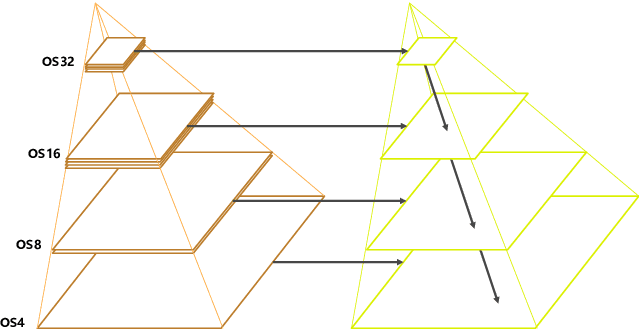
Land-cover classification has long been a hot and difficult challenge in remote sensing community. With massive High-resolution Remote Sensing (HRS) images available, manually and automatically designed Convolutional Neural Networks (CNNs) have already shown their great latent capacity on HRS land-cover classification in recent years. Especially, the former can achieve better performance while the latter is able to generate lightweight architecture. Unfortunately, they both have shortcomings. On the one hand, because manual CNNs are almost proposed for natural image processing, it becomes very redundant and inefficient to process HRS images. On the other hand, nascent Neural Architecture Search (NAS) techniques for dense prediction tasks are mainly based on encoder-decoder architecture, and just focus on the automatic design of the encoder, which makes it still difficult to recover the refined mapping when confronting complicated HRS scenes. To overcome their defects and tackle the HRS land-cover classification problems better, we propose AutoLC which combines the advantages of two methods. First, we devise a hierarchical search space and gain the lightweight encoder underlying gradient-based search strategy. Second, we meticulously design a lightweight but top-performing decoder that is adaptive to the searched encoder of itself. Finally, experimental results on the LoveDA land-cover dataset demonstrate that our AutoLC method outperforms the state-of-art manual and automatic methods with much less computational consumption.