Learning to Race in Extreme Turning Scene with Active Exploration and Gaussian Process Regression-based MPC

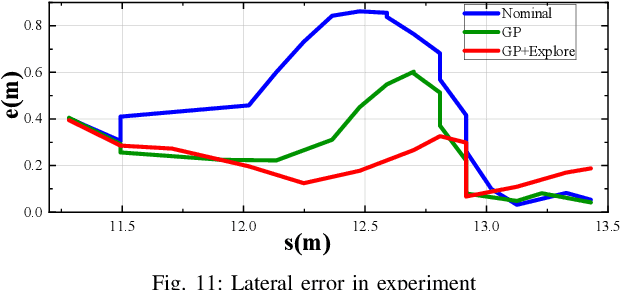
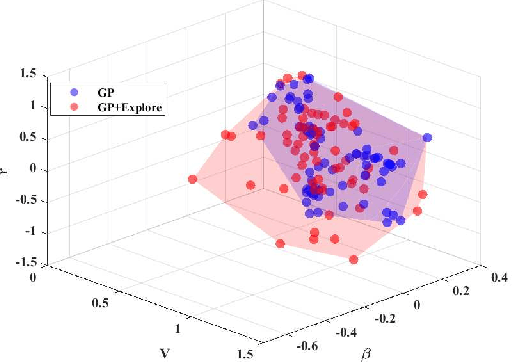
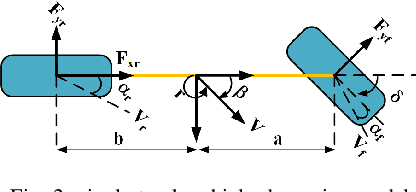
Extreme cornering in racing often induces large side-slip angles, presenting a formidable challenge in vehicle control. To tackle this issue, this paper introduces an Active Exploration with Double GPR (AEDGPR) system. The system initiates by planning a minimum-time trajectory with a Gaussian Process Regression(GPR) compensated model. The planning results show that in the cornering section, the yaw angular velocity and side-slip angle are in opposite directions, indicating that the vehicle is drifting. In response, we develop a drift controller based on Model Predictive Control (MPC) and incorporate Gaussian Process Regression to correct discrepancies in the vehicle dynamics model. Moreover, the covariance from the GPR is employed to actively explore various cornering states, aiming to minimize trajectory tracking errors. The proposed algorithm is validated through simulations on the Simulink-Carsim platform and experiments using a 1/10 scale RC vehicle.

Random Walks: A Review of Algorithms and Applications

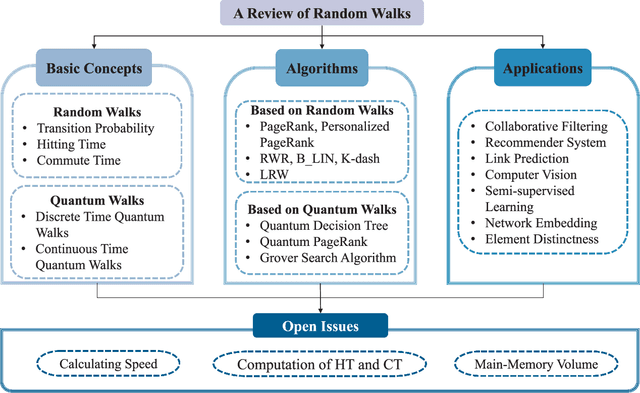
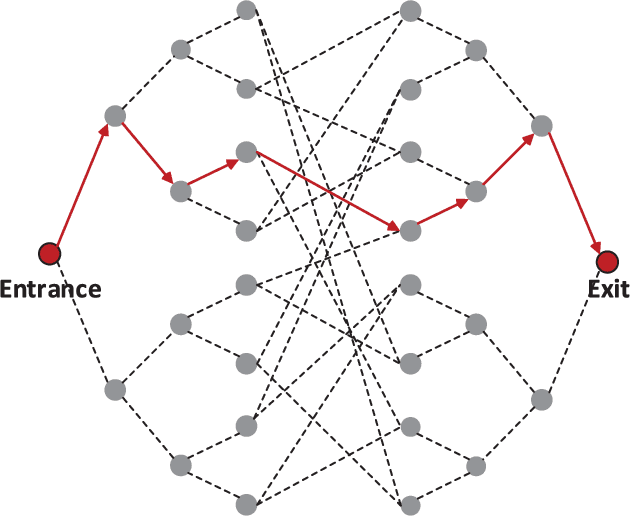
A random walk is known as a random process which describes a path including a succession of random steps in the mathematical space. It has increasingly been popular in various disciplines such as mathematics and computer science. Furthermore, in quantum mechanics, quantum walks can be regarded as quantum analogues of classical random walks. Classical random walks and quantum walks can be used to calculate the proximity between nodes and extract the topology in the network. Various random walk related models can be applied in different fields, which is of great significance to downstream tasks such as link prediction, recommendation, computer vision, semi-supervised learning, and network embedding. In this paper, we aim to provide a comprehensive review of classical random walks and quantum walks. We first review the knowledge of classical random walks and quantum walks, including basic concepts and some typical algorithms. We also compare the algorithms based on quantum walks and classical random walks from the perspective of time complexity. Then we introduce their applications in the field of computer science. Finally we discuss the open issues from the perspectives of efficiency, main-memory volume, and computing time of existing algorithms. This study aims to contribute to this growing area of research by exploring random walks and quantum walks together.