Liangtian Wan
Graph Learning: A Survey
May 03, 2021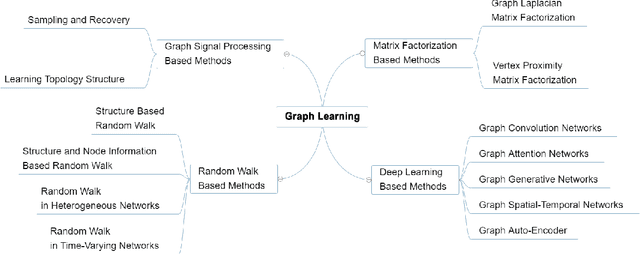
Abstract:Graphs are widely used as a popular representation of the network structure of connected data. Graph data can be found in a broad spectrum of application domains such as social systems, ecosystems, biological networks, knowledge graphs, and information systems. With the continuous penetration of artificial intelligence technologies, graph learning (i.e., machine learning on graphs) is gaining attention from both researchers and practitioners. Graph learning proves effective for many tasks, such as classification, link prediction, and matching. Generally, graph learning methods extract relevant features of graphs by taking advantage of machine learning algorithms. In this survey, we present a comprehensive overview on the state-of-the-art of graph learning. Special attention is paid to four categories of existing graph learning methods, including graph signal processing, matrix factorization, random walk, and deep learning. Major models and algorithms under these categories are reviewed respectively. We examine graph learning applications in areas such as text, images, science, knowledge graphs, and combinatorial optimization. In addition, we discuss several promising research directions in this field.
* 19 pages, 6 figures
Random Walks: A Review of Algorithms and Applications
Aug 09, 2020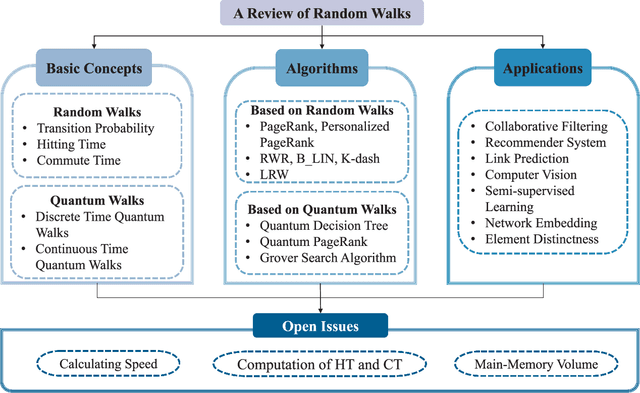

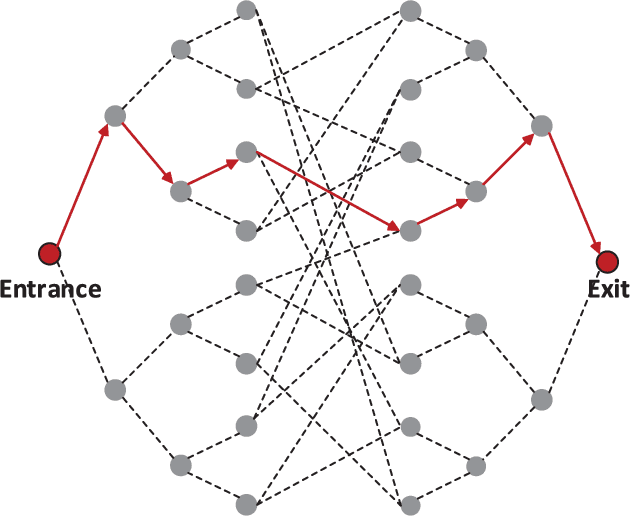

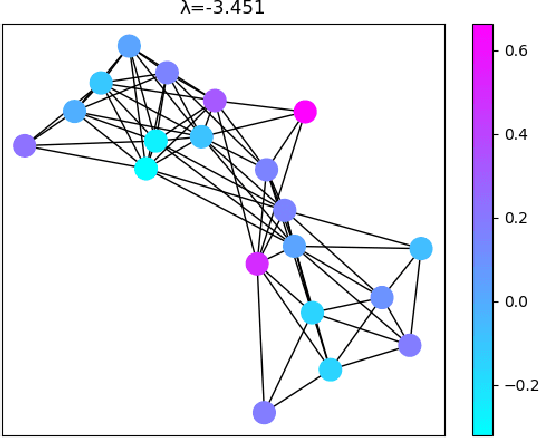
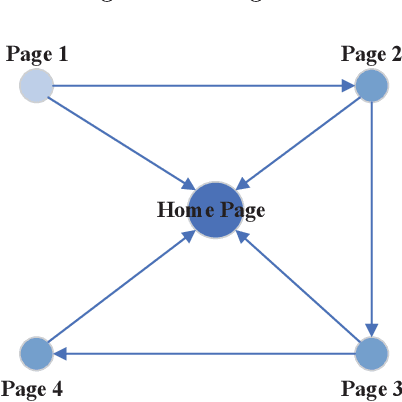
Abstract:A random walk is known as a random process which describes a path including a succession of random steps in the mathematical space. It has increasingly been popular in various disciplines such as mathematics and computer science. Furthermore, in quantum mechanics, quantum walks can be regarded as quantum analogues of classical random walks. Classical random walks and quantum walks can be used to calculate the proximity between nodes and extract the topology in the network. Various random walk related models can be applied in different fields, which is of great significance to downstream tasks such as link prediction, recommendation, computer vision, semi-supervised learning, and network embedding. In this paper, we aim to provide a comprehensive review of classical random walks and quantum walks. We first review the knowledge of classical random walks and quantum walks, including basic concepts and some typical algorithms. We also compare the algorithms based on quantum walks and classical random walks from the perspective of time complexity. Then we introduce their applications in the field of computer science. Finally we discuss the open issues from the perspectives of efficiency, main-memory volume, and computing time of existing algorithms. This study aims to contribute to this growing area of research by exploring random walks and quantum walks together.
* 13 pages, 4 figures
Big Networks: A Survey
Aug 09, 2020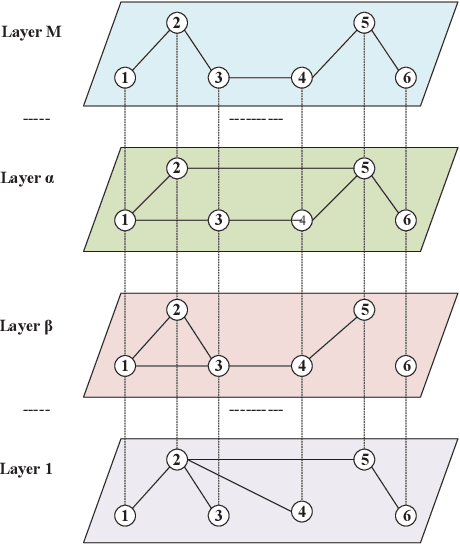


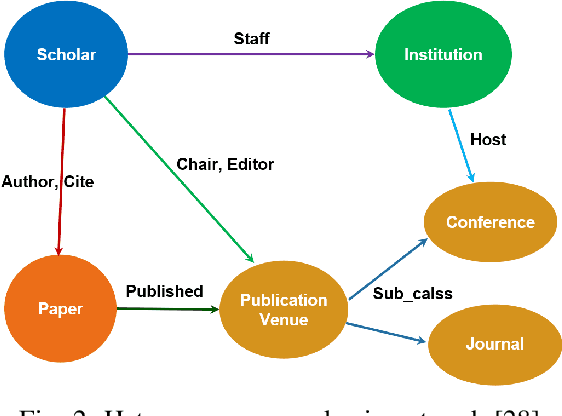
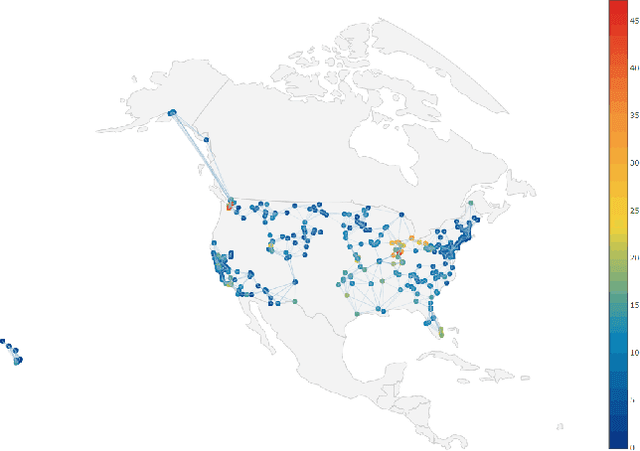
Abstract:A network is a typical expressive form of representing complex systems in terms of vertices and links, in which the pattern of interactions amongst components of the network is intricate. The network can be static that does not change over time or dynamic that evolves through time. The complication of network analysis is different under the new circumstance of network size explosive increasing. In this paper, we introduce a new network science concept called big network. Big networks are generally in large-scale with a complicated and higher-order inner structure. This paper proposes a guideline framework that gives an insight into the major topics in the area of network science from the viewpoint of a big network. We first introduce the structural characteristics of big networks from three levels, which are micro-level, meso-level, and macro-level. We then discuss some state-of-the-art advanced topics of big network analysis. Big network models and related approaches, including ranking methods, partition approaches, as well as network embedding algorithms are systematically introduced. Some typical applications in big networks are then reviewed, such as community detection, link prediction, recommendation, etc. Moreover, we also pinpoint some critical open issues that need to be investigated further.
* 69 pages, 4 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge