Hansong Nie
Random Walks: A Review of Algorithms and Applications
Aug 09, 2020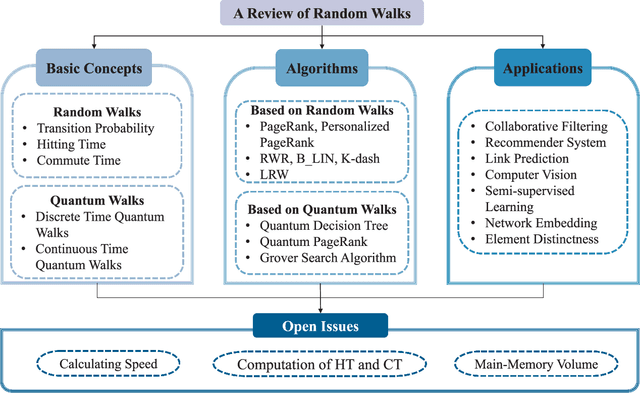


Abstract:A random walk is known as a random process which describes a path including a succession of random steps in the mathematical space. It has increasingly been popular in various disciplines such as mathematics and computer science. Furthermore, in quantum mechanics, quantum walks can be regarded as quantum analogues of classical random walks. Classical random walks and quantum walks can be used to calculate the proximity between nodes and extract the topology in the network. Various random walk related models can be applied in different fields, which is of great significance to downstream tasks such as link prediction, recommendation, computer vision, semi-supervised learning, and network embedding. In this paper, we aim to provide a comprehensive review of classical random walks and quantum walks. We first review the knowledge of classical random walks and quantum walks, including basic concepts and some typical algorithms. We also compare the algorithms based on quantum walks and classical random walks from the perspective of time complexity. Then we introduce their applications in the field of computer science. Finally we discuss the open issues from the perspectives of efficiency, main-memory volume, and computing time of existing algorithms. This study aims to contribute to this growing area of research by exploring random walks and quantum walks together.
* 13 pages, 4 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge