Guillermo Ortiz-Jiménez
On the Difficulty of Constructing a Robust and Publicly-Detectable Watermark
Feb 07, 2025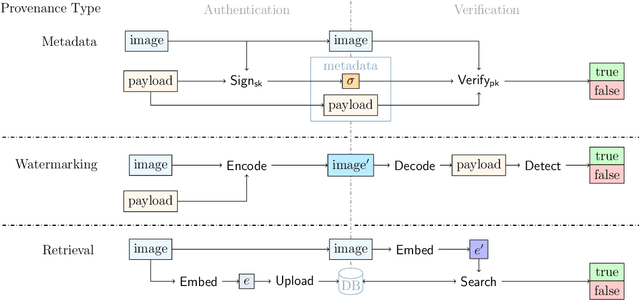
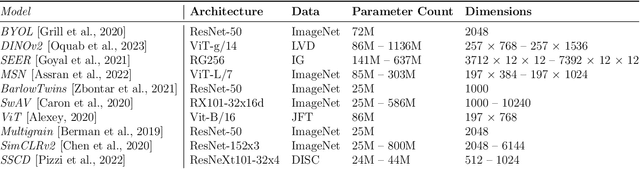
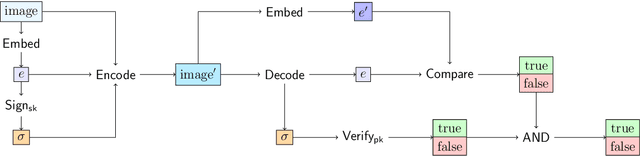
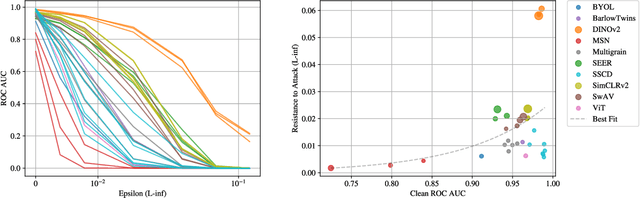
Abstract:This work investigates the theoretical boundaries of creating publicly-detectable schemes to enable the provenance of watermarked imagery. Metadata-based approaches like C2PA provide unforgeability and public-detectability. ML techniques offer robust retrieval and watermarking. However, no existing scheme combines robustness, unforgeability, and public-detectability. In this work, we formally define such a scheme and establish its existence. Although theoretically possible, we find that at present, it is intractable to build certain components of our scheme without a leap in deep learning capabilities. We analyze these limitations and propose research directions that need to be addressed before we can practically realize robust and publicly-verifiable provenance.
Catastrophic overfitting is a bug but also a feature
Jun 16, 2022



Abstract:Despite clear computational advantages in building robust neural networks, adversarial training (AT) using single-step methods is unstable as it suffers from catastrophic overfitting (CO): Networks gain non-trivial robustness during the first stages of adversarial training, but suddenly reach a breaking point where they quickly lose all robustness in just a few iterations. Although some works have succeeded at preventing CO, the different mechanisms that lead to this remarkable failure mode are still poorly understood. In this work, however, we find that the interplay between the structure of the data and the dynamics of AT plays a fundamental role in CO. Specifically, through active interventions on typical datasets of natural images, we establish a causal link between the structure of the data and the onset of CO in single-step AT methods. This new perspective provides important insights into the mechanisms that lead to CO and paves the way towards a better understanding of the general dynamics of robust model construction. The code to reproduce the experiments of this paper can be found at https://github.com/gortizji/co_features .
On the benefits of knowledge distillation for adversarial robustness
Mar 14, 2022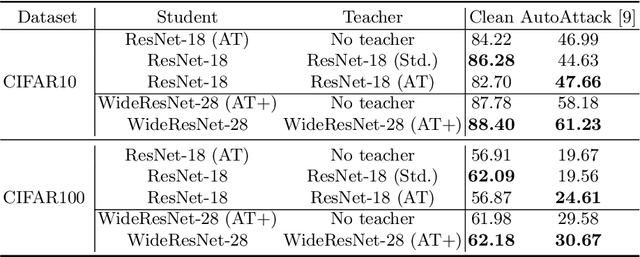
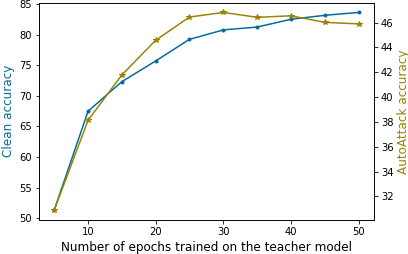
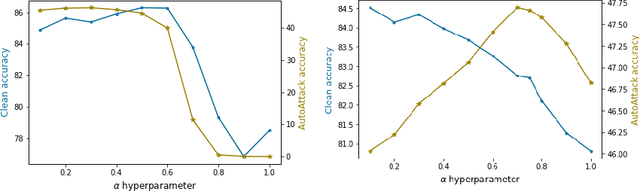
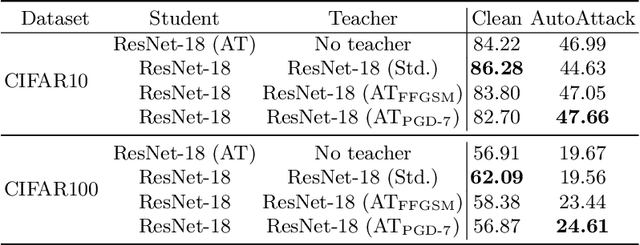
Abstract:Knowledge distillation is normally used to compress a big network, or teacher, onto a smaller one, the student, by training it to match its outputs. Recently, some works have shown that robustness against adversarial attacks can also be distilled effectively to achieve good rates of robustness on mobile-friendly models. In this work, however, we take a different point of view, and show that knowledge distillation can be used directly to boost the performance of state-of-the-art models in adversarial robustness. In this sense, we present a thorough analysis and provide general guidelines to distill knowledge from a robust teacher and boost the clean and adversarial performance of a student model even further. To that end, we present Adversarial Knowledge Distillation (AKD), a new framework to improve a model's robust performance, consisting on adversarially training a student on a mixture of the original labels and the teacher outputs. Through carefully controlled ablation studies, we show that using early-stopping, model ensembles and weak adversarial training are key techniques to maximize performance of the student, and show that these insights generalize across different robust distillation techniques. Finally, we provide insights on the effect of robust knowledge distillation on the dynamics of the student network, and show that AKD mostly improves the calibration of the network and modify its training dynamics on samples that the model finds difficult to learn, or even memorize.
PRIME: A Few Primitives Can Boost Robustness to Common Corruptions
Dec 27, 2021



Abstract:Despite their impressive performance on image classification tasks, deep networks have a hard time generalizing to many common corruptions of their data. To fix this vulnerability, prior works have mostly focused on increasing the complexity of their training pipelines, combining multiple methods, in the name of diversity. However, in this work, we take a step back and follow a principled approach to achieve robustness to common corruptions. We propose PRIME, a general data augmentation scheme that consists of simple families of max-entropy image transformations. We show that PRIME outperforms the prior art for corruption robustness, while its simplicity and plug-and-play nature enables it to be combined with other methods to further boost their robustness. Furthermore, we analyze PRIME to shed light on the importance of the mixing strategy on synthesizing corrupted images, and to reveal the robustness-accuracy trade-offs arising in the context of common corruptions. Finally, we show that the computational efficiency of our method allows it to be easily used in both on-line and off-line data augmentation schemes.
A Structured Dictionary Perspective on Implicit Neural Representations
Dec 03, 2021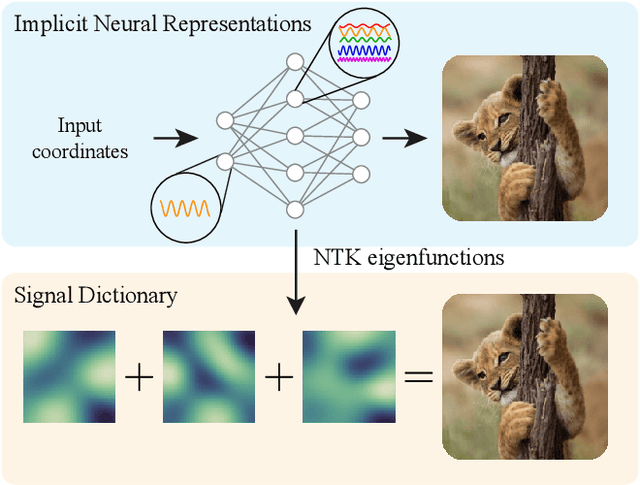
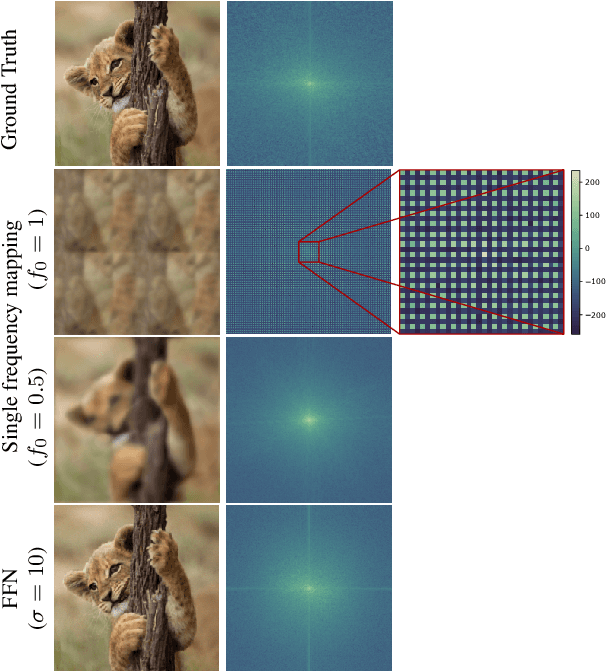
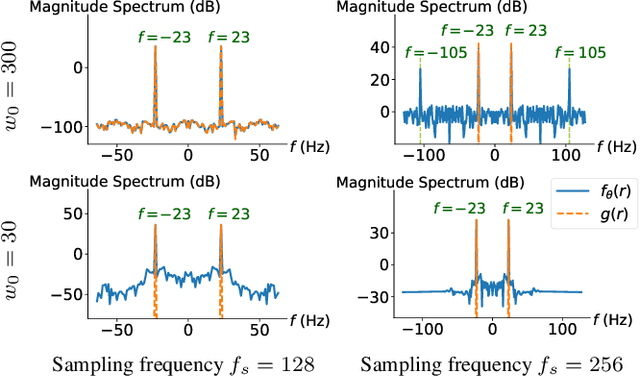
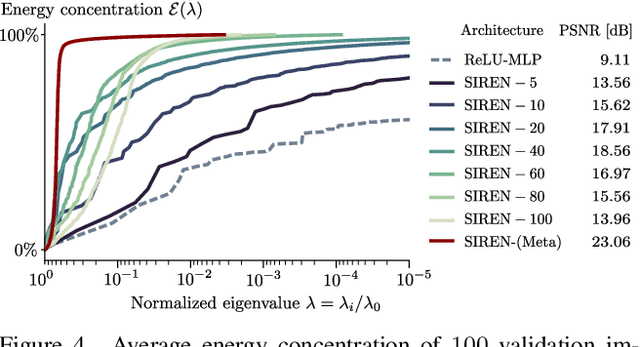
Abstract:Propelled by new designs that permit to circumvent the spectral bias, implicit neural representations (INRs) have recently emerged as a promising alternative to classical discretized representations of signals. Nevertheless, despite their practical success, we still lack a proper theoretical characterization of how INRs represent signals. In this work, we aim to fill this gap, and we propose a novel unified perspective to theoretically analyse INRs. Leveraging results from harmonic analysis and deep learning theory, we show that most INR families are analogous to structured signal dictionaries whose atoms are integer harmonics of the set of initial mapping frequencies. This structure allows INRs to express signals with an exponentially increasing frequency support using a number of parameters that only grows linearly with depth. Afterwards, we explore the inductive bias of INRs exploiting recent results about the empirical neural tangent kernel (NTK). Specifically, we show that the eigenfunctions of the NTK can be seen as dictionary atoms whose inner product with the target signal determines the final performance of their reconstruction. In this regard, we reveal that meta-learning the initialization has a reshaping effect of the NTK analogous to dictionary learning, building dictionary atoms as a combination of the examples seen during meta-training. Our results permit to design and tune novel INR architectures, but can also be of interest for the wider deep learning theory community.
What can linearized neural networks actually say about generalization?
Jun 12, 2021



Abstract:For certain infinitely-wide neural networks, the neural tangent kernel (NTK) theory fully characterizes generalization. However, for the networks used in practice, the empirical NTK represents only a rough first-order approximation of these architectures. Still, a growing body of work keeps leveraging this approximation to successfully analyze important deep learning phenomena and derive algorithms for new applications. In our work, we provide strong empirical evidence to determine the practical validity of such approximation by conducting a systematic comparison of the behaviour of different neural networks and their linear approximations on different tasks. We show that the linear approximations can indeed rank the learning complexity of certain tasks for neural networks, albeit with important nuances. Specifically, we discover that, in contrast to what was previously observed, neural networks do not always perform better than their kernel approximations, and reveal that their performance gap heavily depends on architecture, number of samples and training task. In fact, we show that during training, deep networks increase the alignment of their empirical NTK with the target task, which explains why linear approximations at the end of training can better explain the dynamics of deep networks. Overall, our work provides concrete examples of novel deep learning phenomena which can inspire future theoretical research, as well as provides a new perspective on the use of the NTK approximation in deep learning.
On the choice of graph neural network architectures
Nov 13, 2019


Abstract:Seminal works on graph neural networks have primarily targeted semi-supervised node classification problems with few observed labels and high-dimensional signals. With the development of graph networks, this setup has become a de facto benchmark for a significant body of research. Interestingly, several works have recently shown that graph neural networks do not perform much better than predefined low-pass filters followed by a linear classifier in these particular settings. However, when learning with little data in a high-dimensional space, it is not surprising that simple and heavily regularized learning methods are near-optimal. In this paper, we show empirically that in settings with fewer features and more training data, more complex graph networks significantly outperform simpler architectures, and propose a few insights towards to the proper choice of graph neural networks architectures. We finally outline the importance of using sufficiently diverse benchmarks (including lower dimensional signals as well) when designing and studying new types of graph neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge