The Chicken and Egg Dilemma: Co-optimizing Data and Model Configurations for LLMs

Co-optimizing data and model configurations for training LLMs presents a classic chicken-and-egg dilemma: The best training data configuration (e.g., data mixture) for a downstream task depends on the chosen model configuration (e.g., model architecture), and vice versa. However, jointly optimizing both data and model configurations is often deemed intractable, and existing methods focus on either data or model optimization without considering their interaction. We introduce JoBS, an approach that uses a scaling-law-inspired performance predictor to aid Bayesian optimization (BO) in jointly optimizing LLM training data and model configurations efficiently. JoBS allocates a portion of the optimization budget to learn an LLM performance predictor that predicts how promising a training configuration is from a small number of training steps. The remaining budget is used to perform BO entirely with the predictor, effectively amortizing the cost of running full-training runs. We study JoBS's average regret and devise the optimal budget allocation to minimize regret. JoBS outperforms existing multi-fidelity BO baselines, as well as data and model optimization approaches across diverse LLM tasks under the same optimization budget.

Uncovering Scaling Laws for Large Language Models via Inverse Problems

Large Language Models (LLMs) are large-scale pretrained models that have achieved remarkable success across diverse domains. These successes have been driven by unprecedented complexity and scale in both data and computations. However, due to the high costs of training such models, brute-force trial-and-error approaches to improve LLMs are not feasible. Inspired by the success of inverse problems in uncovering fundamental scientific laws, this position paper advocates that inverse problems can also efficiently uncover scaling laws that guide the building of LLMs to achieve the desirable performance with significantly better cost-effectiveness.

WaterDrum: Watermarking for Data-centric Unlearning Metric

Large language model (LLM) unlearning is critical in real-world applications where it is necessary to efficiently remove the influence of private, copyrighted, or harmful data from some users. However, existing utility-centric unlearning metrics (based on model utility) may fail to accurately evaluate the extent of unlearning in realistic settings such as when (a) the forget and retain set have semantically similar content, (b) retraining the model from scratch on the retain set is impractical, and/or (c) the model owner can improve the unlearning metric without directly performing unlearning on the LLM. This paper presents the first data-centric unlearning metric for LLMs called WaterDrum that exploits robust text watermarking for overcoming these limitations. We also introduce new benchmark datasets for LLM unlearning that contain varying levels of similar data points and can be used to rigorously evaluate unlearning algorithms using WaterDrum. Our code is available at https://github.com/lululu008/WaterDrum and our new benchmark datasets are released at https://huggingface.co/datasets/Glow-AI/WaterDrum-Ax.

PIED: Physics-Informed Experimental Design for Inverse Problems

In many science and engineering settings, system dynamics are characterized by governing PDEs, and a major challenge is to solve inverse problems (IPs) where unknown PDE parameters are inferred based on observational data gathered under limited budget. Due to the high costs of setting up and running experiments, experimental design (ED) is often done with the help of PDE simulations to optimize for the most informative design parameters to solve such IPs, prior to actual data collection. This process of optimizing design parameters is especially critical when the budget and other practical constraints make it infeasible to adjust the design parameters between trials during the experiments. However, existing experimental design (ED) methods tend to require sequential and frequent design parameter adjustments between trials. Furthermore, they also have significant computational bottlenecks due to the need for complex numerical simulations for PDEs, and do not exploit the advantages provided by physics informed neural networks (PINNs), such as its meshless solutions, differentiability, and amortized training. This work presents PIED, the first ED framework that makes use of PINNs in a fully differentiable architecture to perform continuous optimization of design parameters for IPs for one-shot deployments. PIED overcomes existing methods' computational bottlenecks through parallelized computation and meta-learning of PINN parameter initialization, and proposes novel methods to effectively take into account PINN training dynamics in optimizing the ED parameters. Through experiments based on noisy simulated data and even real world experimental data, we empirically show that given limited observation budget, PIED significantly outperforms existing ED methods in solving IPs, including challenging settings where the inverse parameters are unknown functions rather than just finite-dimensional.

Dipper: Diversity in Prompts for Producing Large Language Model Ensembles in Reasoning tasks

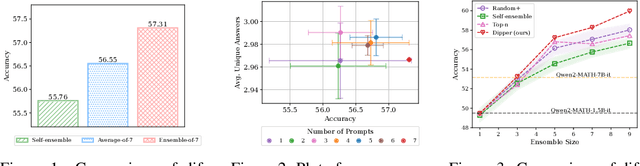
Large Language Models still encounter substantial challenges in reasoning tasks, especially for smaller models, which many users may be restricted to due to resource constraints (e.g. GPU memory restrictions). Inference-time methods to boost LLM performance, such as prompting methods to invoke certain reasoning pathways in responses, have been shown effective in past works, though they largely rely on sequential queries. The ensemble method, which consists of multiple constituent models running in parallel, is a promising approach to achieving better inference-time performance, especially given recent developments that enabled significant speed-ups in LLM batch inference. In this work, we propose a novel, training-free LLM ensemble framework where a single LLM model is fed an optimized, diverse set of prompts in parallel, effectively producing an ensemble at inference time to achieve performance improvement in reasoning tasks. We empirically demonstrate that our method leads to significant gains on math reasoning tasks, e.g., on MATH, where our ensemble consisting of a few small models (e.g., three Qwen2-MATH-1.5B-it models) can outperform a larger model (e.g., Qwen2-MATH-7B-it).

Waterfall: Framework for Robust and Scalable Text Watermarking

Protecting intellectual property (IP) of text such as articles and code is increasingly important, especially as sophisticated attacks become possible, such as paraphrasing by large language models (LLMs) or even unauthorized training of LLMs on copyrighted text to infringe such IP. However, existing text watermarking methods are not robust enough against such attacks nor scalable to millions of users for practical implementation. In this paper, we propose Waterfall, the first training-free framework for robust and scalable text watermarking applicable across multiple text types (e.g., articles, code) and languages supportable by LLMs, for general text and LLM data provenance. Waterfall comprises several key innovations, such as being the first to use LLM as paraphrasers for watermarking along with a novel combination of techniques that are surprisingly effective in achieving robust verifiability and scalability. We empirically demonstrate that Waterfall achieves significantly better scalability, robust verifiability, and computational efficiency compared to SOTA article-text watermarking methods, and also showed how it could be directly applied to the watermarking of code.

Data-Centric AI in the Age of Large Language Models

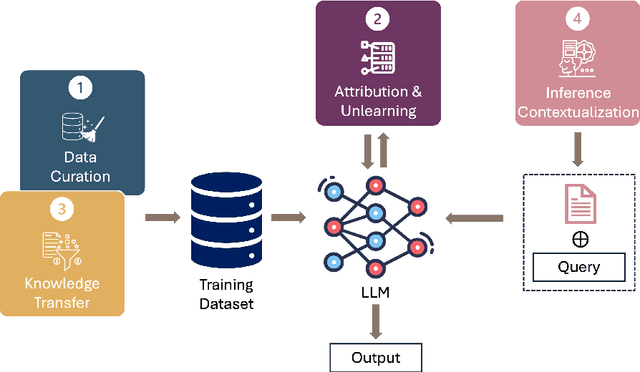
This position paper proposes a data-centric viewpoint of AI research, focusing on large language models (LLMs). We start by making the key observation that data is instrumental in the developmental (e.g., pretraining and fine-tuning) and inferential stages (e.g., in-context learning) of LLMs, and yet it receives disproportionally low attention from the research community. We identify four specific scenarios centered around data, covering data-centric benchmarks and data curation, data attribution, knowledge transfer, and inference contextualization. In each scenario, we underscore the importance of data, highlight promising research directions, and articulate the potential impacts on the research community and, where applicable, the society as a whole. For instance, we advocate for a suite of data-centric benchmarks tailored to the scale and complexity of data for LLMs. These benchmarks can be used to develop new data curation methods and document research efforts and results, which can help promote openness and transparency in AI and LLM research.

PINNACLE: PINN Adaptive ColLocation and Experimental points selection

Physics-Informed Neural Networks (PINNs), which incorporate PDEs as soft constraints, train with a composite loss function that contains multiple training point types: different types of collocation points chosen during training to enforce each PDE and initial/boundary conditions, and experimental points which are usually costly to obtain via experiments or simulations. Training PINNs using this loss function is challenging as it typically requires selecting large numbers of points of different types, each with different training dynamics. Unlike past works that focused on the selection of either collocation or experimental points, this work introduces PINN Adaptive ColLocation and Experimental points selection (PINNACLE), the first algorithm that jointly optimizes the selection of all training point types, while automatically adjusting the proportion of collocation point types as training progresses. PINNACLE uses information on the interaction among training point types, which had not been considered before, based on an analysis of PINN training dynamics via the Neural Tangent Kernel (NTK). We theoretically show that the criterion used by PINNACLE is related to the PINN generalization error, and empirically demonstrate that PINNACLE is able to outperform existing point selection methods for forward, inverse, and transfer learning problems.

Quantum Bayesian Optimization

Kernelized bandits, also known as Bayesian optimization (BO), has been a prevalent method for optimizing complicated black-box reward functions. Various BO algorithms have been theoretically shown to enjoy upper bounds on their cumulative regret which are sub-linear in the number T of iterations, and a regret lower bound of Omega(sqrt(T)) has been derived which represents the unavoidable regrets for any classical BO algorithm. Recent works on quantum bandits have shown that with the aid of quantum computing, it is possible to achieve tighter regret upper bounds better than their corresponding classical lower bounds. However, these works are restricted to either multi-armed or linear bandits, and are hence not able to solve sophisticated real-world problems with non-linear reward functions. To this end, we introduce the quantum-Gaussian process-upper confidence bound (Q-GP-UCB) algorithm. To the best of our knowledge, our Q-GP-UCB is the first BO algorithm able to achieve a regret upper bound of O(polylog T), which is significantly smaller than its regret lower bound of Omega(sqrt(T)) in the classical setting. Moreover, thanks to our novel analysis of the confidence ellipsoid, our Q-GP-UCB with the linear kernel achieves a smaller regret than the quantum linear UCB algorithm from the previous work. We use simulations, as well as an experiment using a real quantum computer, to verify that the theoretical quantum speedup achieved by our Q-GP-UCB is also potentially relevant in practice.