Giacomo Camposampiero
Can Large Reasoning Models do Analogical Reasoning under Perceptual Uncertainty?
Mar 14, 2025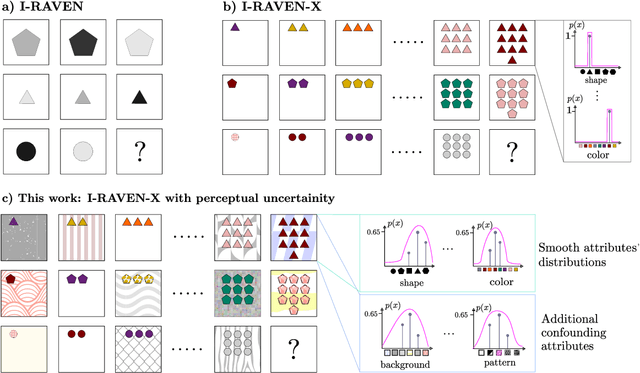
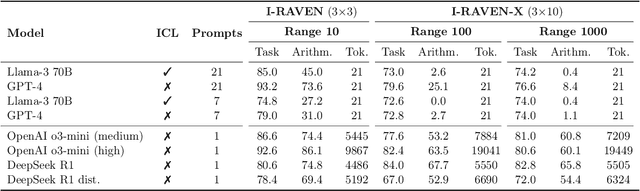
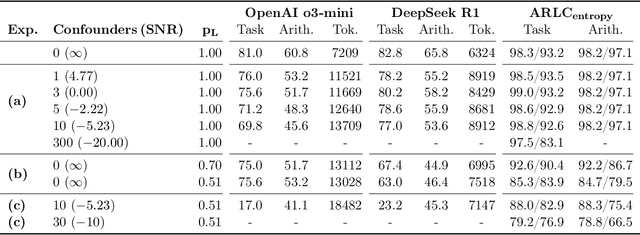
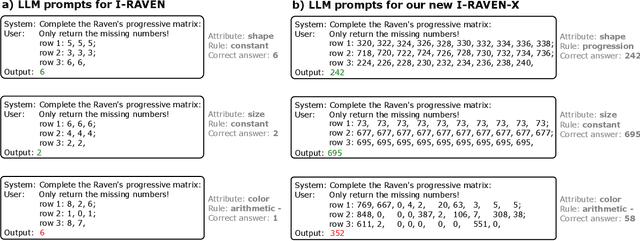
Abstract:This work presents a first evaluation of two state-of-the-art Large Reasoning Models (LRMs), OpenAI's o3-mini and DeepSeek R1, on analogical reasoning, focusing on well-established nonverbal human IQ tests based on Raven's progressive matrices. We benchmark with the I-RAVEN dataset and its more difficult extension, I-RAVEN-X, which tests the ability to generalize to longer reasoning rules and ranges of the attribute values. To assess the influence of visual uncertainties on these nonverbal analogical reasoning tests, we extend the I-RAVEN-X dataset, which otherwise assumes an oracle perception. We adopt a two-fold strategy to simulate this imperfect visual perception: 1) we introduce confounding attributes which, being sampled at random, do not contribute to the prediction of the correct answer of the puzzles and 2) smoothen the distributions of the input attributes' values. We observe a sharp decline in OpenAI's o3-mini task accuracy, dropping from 86.6% on the original I-RAVEN to just 17.0% -- approaching random chance -- on the more challenging I-RAVEN-X, which increases input length and range and emulates perceptual uncertainty. This drop occurred despite spending 3.4x more reasoning tokens. A similar trend is also observed for DeepSeek R1: from 80.6% to 23.2%. On the other hand, a neuro-symbolic probabilistic abductive model, ARLC, that achieves state-of-the-art performances on I-RAVEN, can robustly reason under all these out-of-distribution tests, maintaining strong accuracy with only a modest reduction from 98.6% to 88.0%. Our code is available at https://github.com/IBM/raven-large-language-models.
On the Expressiveness and Length Generalization of Selective State-Space Models on Regular Languages
Dec 26, 2024



Abstract:Selective state-space models (SSMs) are an emerging alternative to the Transformer, offering the unique advantage of parallel training and sequential inference. Although these models have shown promising performance on a variety of tasks, their formal expressiveness and length generalization properties remain underexplored. In this work, we provide insight into the workings of selective SSMs by analyzing their expressiveness and length generalization performance on regular language tasks, i.e., finite-state automaton (FSA) emulation. We address certain limitations of modern SSM-based architectures by introducing the Selective Dense State-Space Model (SD-SSM), the first selective SSM that exhibits perfect length generalization on a set of various regular language tasks using a single layer. It utilizes a dictionary of dense transition matrices, a softmax selection mechanism that creates a convex combination of dictionary matrices at each time step, and a readout consisting of layer normalization followed by a linear map. We then proceed to evaluate variants of diagonal selective SSMs by considering their empirical performance on commutative and non-commutative automata. We explain the experimental results with theoretical considerations. Our code is available at https://github.com/IBM/selective-dense-state-space-model.
Towards Learning to Reason: Comparing LLMs with Neuro-Symbolic on Arithmetic Relations in Abstract Reasoning
Dec 07, 2024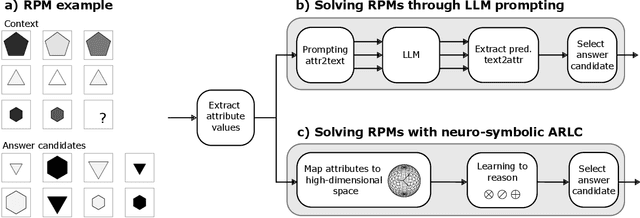
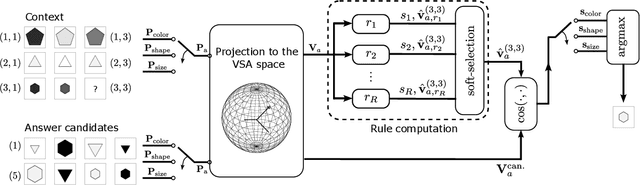
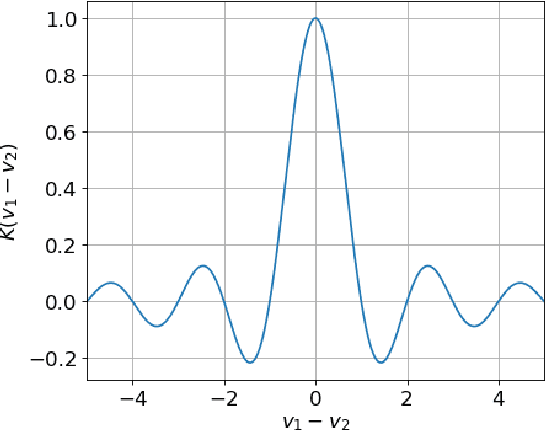
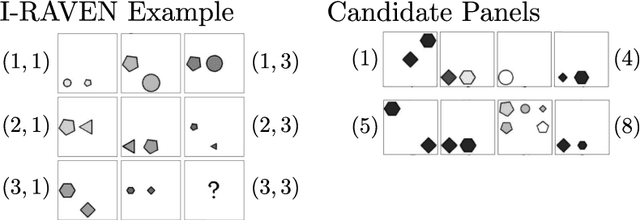
Abstract:This work compares large language models (LLMs) and neuro-symbolic approaches in solving Raven's progressive matrices (RPM), a visual abstract reasoning test that involves the understanding of mathematical rules such as progression or arithmetic addition. Providing the visual attributes directly as textual prompts, which assumes an oracle visual perception module, allows us to measure the model's abstract reasoning capability in isolation. Despite providing such compositionally structured representations from the oracle visual perception and advanced prompting techniques, both GPT-4 and Llama-3 70B cannot achieve perfect accuracy on the center constellation of the I-RAVEN dataset. Our analysis reveals that the root cause lies in the LLM's weakness in understanding and executing arithmetic rules. As a potential remedy, we analyze the Abductive Rule Learner with Context-awareness (ARLC), a neuro-symbolic approach that learns to reason with vector-symbolic architectures (VSAs). Here, concepts are represented with distributed vectors s.t. dot products between encoded vectors define a similarity kernel, and simple element-wise operations on the vectors perform addition/subtraction on the encoded values. We find that ARLC achieves almost perfect accuracy on the center constellation of I-RAVEN, demonstrating a high fidelity in arithmetic rules. To stress the length generalization capabilities of the models, we extend the RPM tests to larger matrices (3x10 instead of typical 3x3) and larger dynamic ranges of the attribute values (from 10 up to 1000). We find that the LLM's accuracy of solving arithmetic rules drops to sub-10%, especially as the dynamic range expands, while ARLC can maintain a high accuracy due to emulating symbolic computations on top of properly distributed representations. Our code is available at https://github.com/IBM/raven-large-language-models.
Kernel Approximation using Analog In-Memory Computing
Nov 05, 2024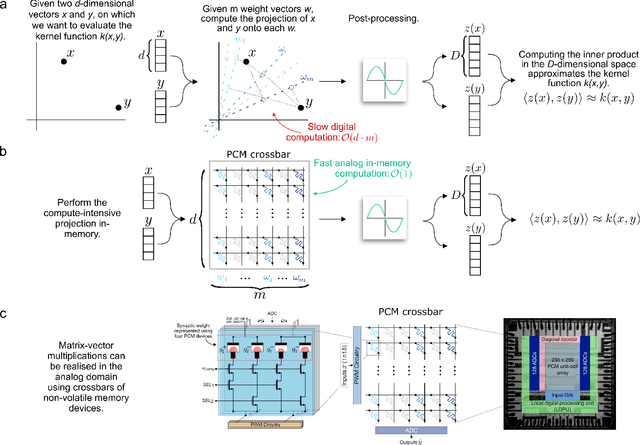
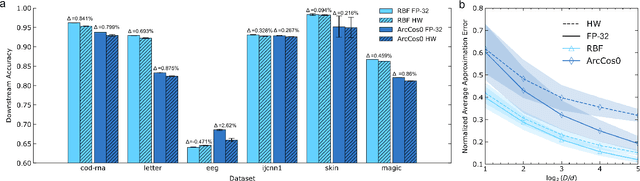
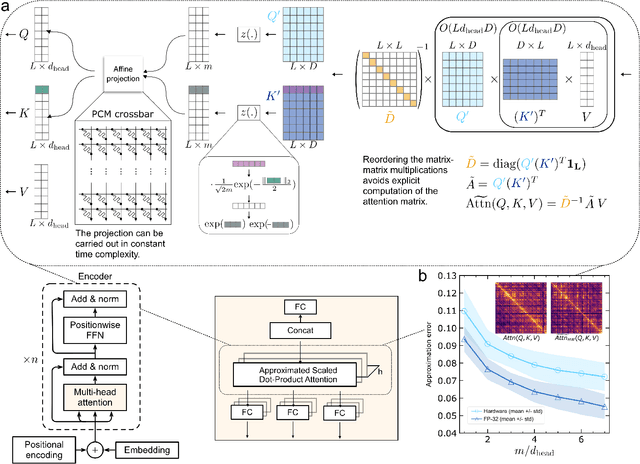
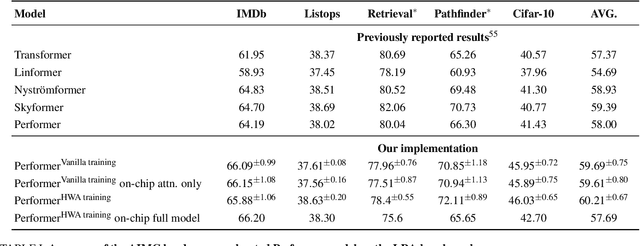
Abstract:Kernel functions are vital ingredients of several machine learning algorithms, but often incur significant memory and computational costs. We introduce an approach to kernel approximation in machine learning algorithms suitable for mixed-signal Analog In-Memory Computing (AIMC) architectures. Analog In-Memory Kernel Approximation addresses the performance bottlenecks of conventional kernel-based methods by executing most operations in approximate kernel methods directly in memory. The IBM HERMES Project Chip, a state-of-the-art phase-change memory based AIMC chip, is utilized for the hardware demonstration of kernel approximation. Experimental results show that our method maintains high accuracy, with less than a 1% drop in kernel-based ridge classification benchmarks and within 1% accuracy on the Long Range Arena benchmark for kernelized attention in Transformer neural networks. Compared to traditional digital accelerators, our approach is estimated to deliver superior energy efficiency and lower power consumption. These findings highlight the potential of heterogeneous AIMC architectures to enhance the efficiency and scalability of machine learning applications.
Terminating Differentiable Tree Experts
Jul 02, 2024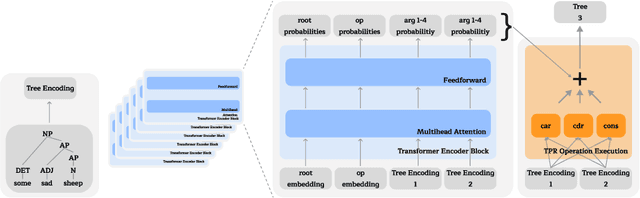

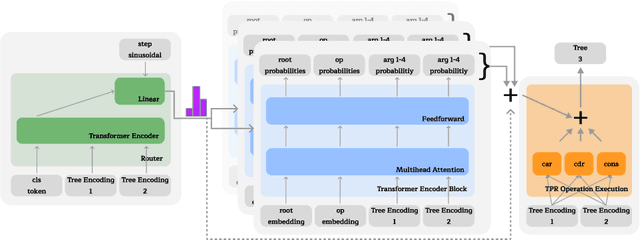

Abstract:We advance the recently proposed neuro-symbolic Differentiable Tree Machine, which learns tree operations using a combination of transformers and Tensor Product Representations. We investigate the architecture and propose two key components. We first remove a series of different transformer layers that are used in every step by introducing a mixture of experts. This results in a Differentiable Tree Experts model with a constant number of parameters for any arbitrary number of steps in the computation, compared to the previous method in the Differentiable Tree Machine with a linear growth. Given this flexibility in the number of steps, we additionally propose a new termination algorithm to provide the model the power to choose how many steps to make automatically. The resulting Terminating Differentiable Tree Experts model sluggishly learns to predict the number of steps without an oracle. It can do so while maintaining the learning capabilities of the model, converging to the optimal amount of steps.
Towards Learning Abductive Reasoning using VSA Distributed Representations
Jun 27, 2024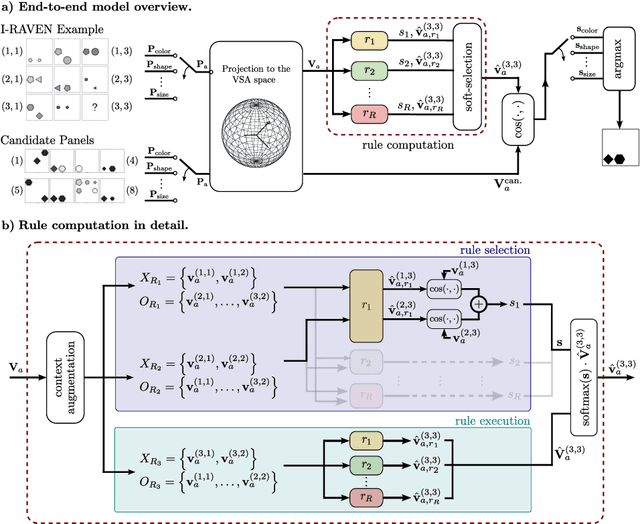

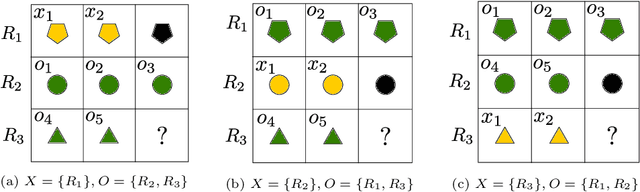
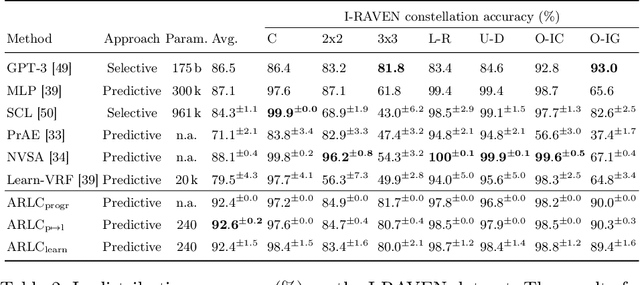
Abstract:We introduce the Abductive Rule Learner with Context-awareness (ARLC), a model that solves abstract reasoning tasks based on Learn-VRF. ARLC features a novel and more broadly applicable training objective for abductive reasoning, resulting in better interpretability and higher accuracy when solving Raven's progressive matrices (RPM). ARLC allows both programming domain knowledge and learning the rules underlying a data distribution. We evaluate ARLC on the I-RAVEN dataset, showcasing state-of-the-art accuracy across both in-distribution and out-of-distribution (unseen attribute-rule pairs) tests. ARLC surpasses neuro-symbolic and connectionist baselines, including large language models, despite having orders of magnitude fewer parameters. We show ARLC's robustness to post-programming training by incrementally learning from examples on top of programmed knowledge, which only improves its performance and does not result in catastrophic forgetting of the programmed solution. We validate ARLC's seamless transfer learning from a 2x2 RPM constellation to unseen constellations. Our code is available at https://github.com/IBM/abductive-rule-learner-with-context-awareness.
Limits of Transformer Language Models on Learning Algorithmic Compositions
Feb 13, 2024



Abstract:We analyze the capabilities of Transformer language models on learning discrete algorithms. To this end, we introduce two new tasks demanding the composition of several discrete sub-tasks. On both training LLaMA models from scratch and prompting on GPT-4 and Gemini we measure learning compositions of learned primitives. We observe that the compositional capabilities of state-of-the-art Transformer language models are very limited and sample-wise scale worse than relearning all sub-tasks for a new algorithmic composition. We also present a theorem in complexity theory, showing that gradient descent on memorizing feedforward models can be exponentially data inefficient.
Visual Abstraction and Reasoning through Language
Mar 07, 2023Abstract:While Artificial Intelligence (AI) models have achieved human or even superhuman performance in narrowly defined applications, they still struggle to show signs of broader and more flexible intelligence. The Abstraction and Reasoning Corpus (ARC), introduced by Fran\c{c}ois Chollet, aims to assess how close AI systems are to human-like cognitive abilities. Most current approaches rely on carefully handcrafted domain-specific languages (DSLs), which are used to brute-force solutions to the tasks present in ARC. In this work, we propose a general framework for solving ARC based on natural language descriptions of the tasks. While not yet beating state-of-the-art DSL models on ARC, we demonstrate the immense potential of our approach hinted at by the ability to solve previously unsolved tasks.
The effectiveness of factorization and similarity blending
Sep 16, 2022

Abstract:Collaborative Filtering (CF) is a widely used technique which allows to leverage past users' preferences data to identify behavioural patterns and exploit them to predict custom recommendations. In this work, we illustrate our review of different CF techniques in the context of the Computational Intelligence Lab (CIL) CF project at ETH Z\"urich. After evaluating the performances of the individual models, we show that blending factorization-based and similarity-based approaches can lead to a significant error decrease (-9.4%) on the best-performing stand-alone model. Moreover, we propose a novel stochastic extension of a similarity model, SCSR, which consistently reduce the asymptotic complexity of the original algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge