Structured Sparse Transition Matrices to Enable State Tracking in State-Space Models

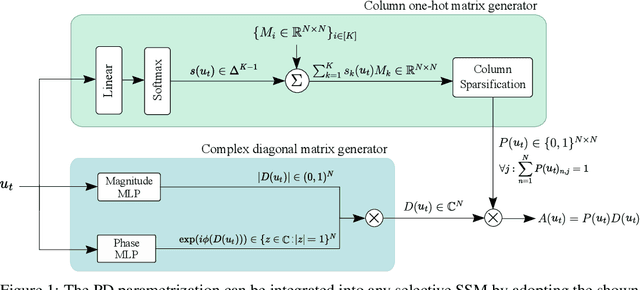
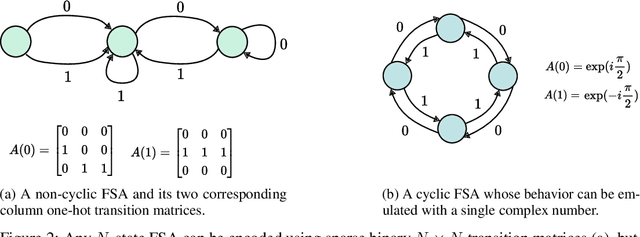
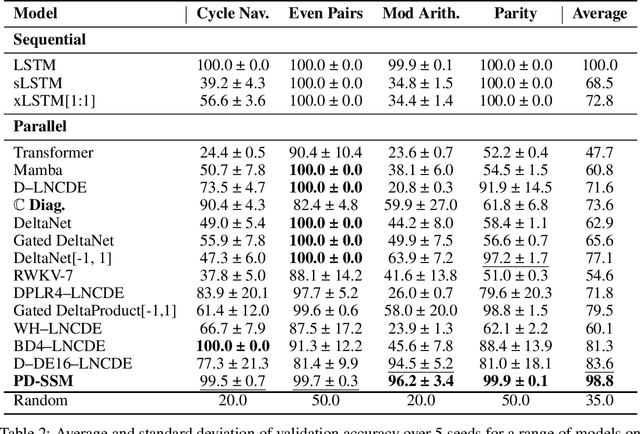
Modern state-space models (SSMs) often utilize transition matrices which enable efficient computation but pose restrictions on the model's expressivity, as measured in terms of the ability to emulate finite-state automata (FSA). While unstructured transition matrices are optimal in terms of expressivity, they come at a prohibitively high compute and memory cost even for moderate state sizes. We propose a structured sparse parametrization of transition matrices in SSMs that enables FSA state tracking with optimal state size and depth, while keeping the computational cost of the recurrence comparable to that of diagonal SSMs. Our method, PD-SSM, parametrizes the transition matrix as the product of a column one-hot matrix ($P$) and a complex-valued diagonal matrix ($D$). Consequently, the computational cost of parallel scans scales linearly with the state size. Theoretically, the model is BIBO-stable and can emulate any $N$-state FSA with one layer of dimension $N$ and a linear readout of size $N \times N$, significantly improving on all current structured SSM guarantees. Experimentally, the model significantly outperforms a wide collection of modern SSM variants on various FSA state tracking tasks. On multiclass time-series classification, the performance is comparable to that of neural controlled differential equations, a paradigm explicitly built for time-series analysis. Finally, we integrate PD-SSM into a hybrid Transformer-SSM architecture and demonstrate that the model can effectively track the states of a complex FSA in which transitions are encoded as a set of variable-length English sentences. The code is available at https://github.com/IBM/expressive-sparse-state-space-model

On the Expressiveness and Length Generalization of Selective State-Space Models on Regular Languages

Selective state-space models (SSMs) are an emerging alternative to the Transformer, offering the unique advantage of parallel training and sequential inference. Although these models have shown promising performance on a variety of tasks, their formal expressiveness and length generalization properties remain underexplored. In this work, we provide insight into the workings of selective SSMs by analyzing their expressiveness and length generalization performance on regular language tasks, i.e., finite-state automaton (FSA) emulation. We address certain limitations of modern SSM-based architectures by introducing the Selective Dense State-Space Model (SD-SSM), the first selective SSM that exhibits perfect length generalization on a set of various regular language tasks using a single layer. It utilizes a dictionary of dense transition matrices, a softmax selection mechanism that creates a convex combination of dictionary matrices at each time step, and a readout consisting of layer normalization followed by a linear map. We then proceed to evaluate variants of diagonal selective SSMs by considering their empirical performance on commutative and non-commutative automata. We explain the experimental results with theoretical considerations. Our code is available at https://github.com/IBM/selective-dense-state-space-model.

Terminating Differentiable Tree Experts

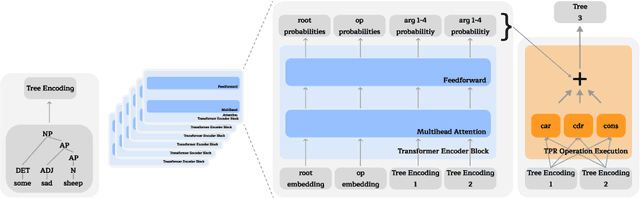
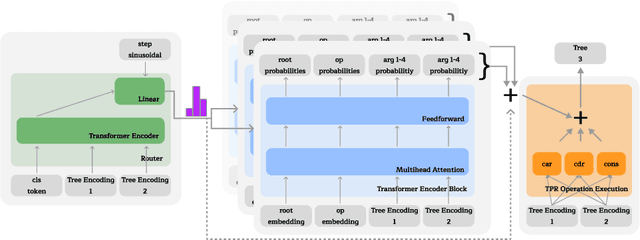
We advance the recently proposed neuro-symbolic Differentiable Tree Machine, which learns tree operations using a combination of transformers and Tensor Product Representations. We investigate the architecture and propose two key components. We first remove a series of different transformer layers that are used in every step by introducing a mixture of experts. This results in a Differentiable Tree Experts model with a constant number of parameters for any arbitrary number of steps in the computation, compared to the previous method in the Differentiable Tree Machine with a linear growth. Given this flexibility in the number of steps, we additionally propose a new termination algorithm to provide the model the power to choose how many steps to make automatically. The resulting Terminating Differentiable Tree Experts model sluggishly learns to predict the number of steps without an oracle. It can do so while maintaining the learning capabilities of the model, converging to the optimal amount of steps.

Towards Learning Abductive Reasoning using VSA Distributed Representations

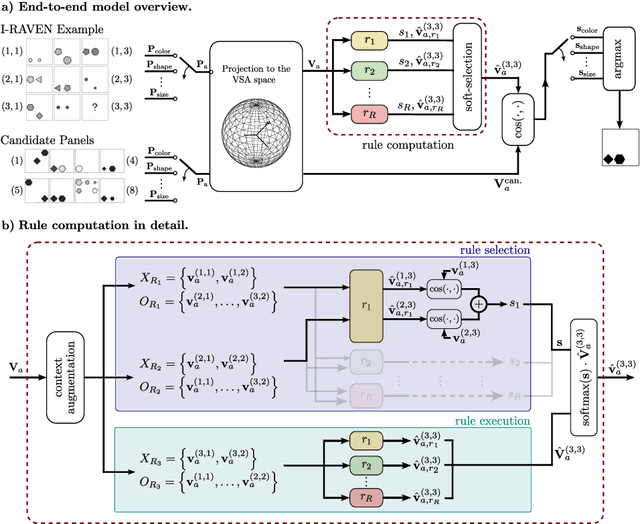
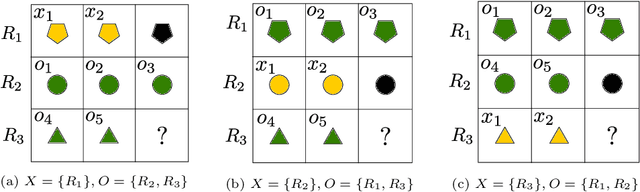
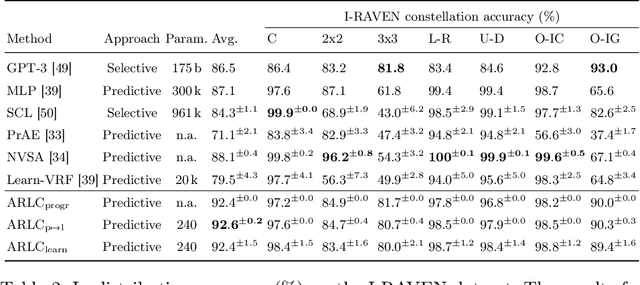
We introduce the Abductive Rule Learner with Context-awareness (ARLC), a model that solves abstract reasoning tasks based on Learn-VRF. ARLC features a novel and more broadly applicable training objective for abductive reasoning, resulting in better interpretability and higher accuracy when solving Raven's progressive matrices (RPM). ARLC allows both programming domain knowledge and learning the rules underlying a data distribution. We evaluate ARLC on the I-RAVEN dataset, showcasing state-of-the-art accuracy across both in-distribution and out-of-distribution (unseen attribute-rule pairs) tests. ARLC surpasses neuro-symbolic and connectionist baselines, including large language models, despite having orders of magnitude fewer parameters. We show ARLC's robustness to post-programming training by incrementally learning from examples on top of programmed knowledge, which only improves its performance and does not result in catastrophic forgetting of the programmed solution. We validate ARLC's seamless transfer learning from a 2x2 RPM constellation to unseen constellations. Our code is available at https://github.com/IBM/abductive-rule-learner-with-context-awareness.