Terminating Differentiable Tree Experts
Paper and Code
Jul 02, 2024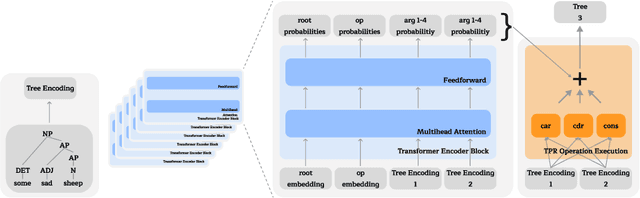

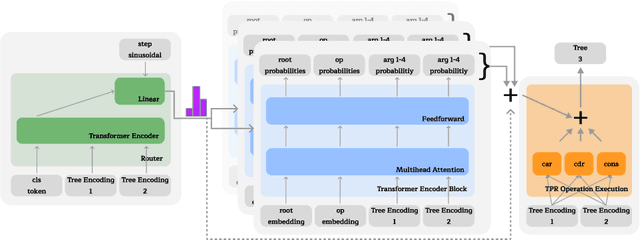

We advance the recently proposed neuro-symbolic Differentiable Tree Machine, which learns tree operations using a combination of transformers and Tensor Product Representations. We investigate the architecture and propose two key components. We first remove a series of different transformer layers that are used in every step by introducing a mixture of experts. This results in a Differentiable Tree Experts model with a constant number of parameters for any arbitrary number of steps in the computation, compared to the previous method in the Differentiable Tree Machine with a linear growth. Given this flexibility in the number of steps, we additionally propose a new termination algorithm to provide the model the power to choose how many steps to make automatically. The resulting Terminating Differentiable Tree Experts model sluggishly learns to predict the number of steps without an oracle. It can do so while maintaining the learning capabilities of the model, converging to the optimal amount of steps.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge