Towards Learning to Reason: Comparing LLMs with Neuro-Symbolic on Arithmetic Relations in Abstract Reasoning
Paper and Code
Dec 07, 2024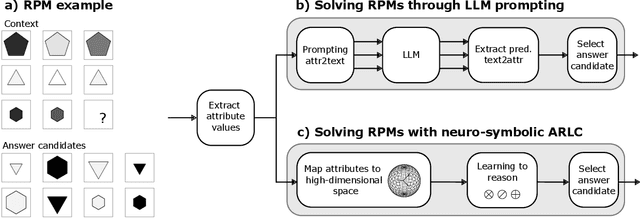
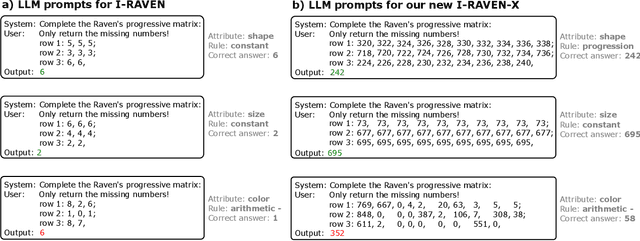
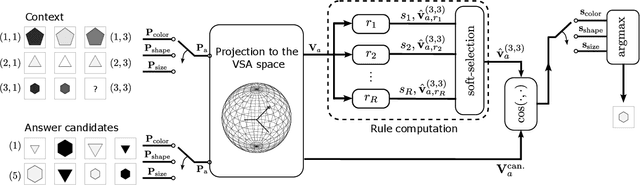
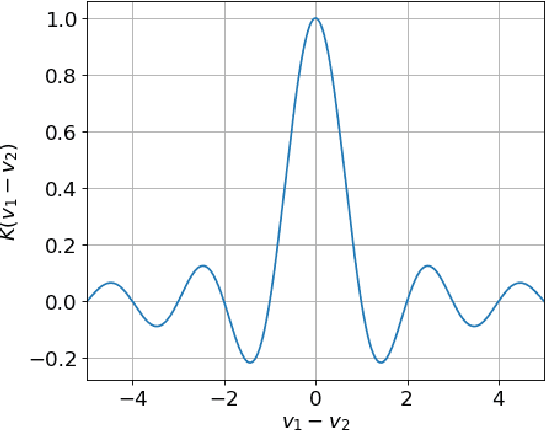
This work compares large language models (LLMs) and neuro-symbolic approaches in solving Raven's progressive matrices (RPM), a visual abstract reasoning test that involves the understanding of mathematical rules such as progression or arithmetic addition. Providing the visual attributes directly as textual prompts, which assumes an oracle visual perception module, allows us to measure the model's abstract reasoning capability in isolation. Despite providing such compositionally structured representations from the oracle visual perception and advanced prompting techniques, both GPT-4 and Llama-3 70B cannot achieve perfect accuracy on the center constellation of the I-RAVEN dataset. Our analysis reveals that the root cause lies in the LLM's weakness in understanding and executing arithmetic rules. As a potential remedy, we analyze the Abductive Rule Learner with Context-awareness (ARLC), a neuro-symbolic approach that learns to reason with vector-symbolic architectures (VSAs). Here, concepts are represented with distributed vectors s.t. dot products between encoded vectors define a similarity kernel, and simple element-wise operations on the vectors perform addition/subtraction on the encoded values. We find that ARLC achieves almost perfect accuracy on the center constellation of I-RAVEN, demonstrating a high fidelity in arithmetic rules. To stress the length generalization capabilities of the models, we extend the RPM tests to larger matrices (3x10 instead of typical 3x3) and larger dynamic ranges of the attribute values (from 10 up to 1000). We find that the LLM's accuracy of solving arithmetic rules drops to sub-10%, especially as the dynamic range expands, while ARLC can maintain a high accuracy due to emulating symbolic computations on top of properly distributed representations. Our code is available at https://github.com/IBM/raven-large-language-models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge