Probabilistic Satisfaction of Temporal Logic Constraints in Reinforcement Learning via Adaptive Policy-Switching

Constrained Reinforcement Learning (CRL) is a subset of machine learning that introduces constraints into the traditional reinforcement learning (RL) framework. Unlike conventional RL which aims solely to maximize cumulative rewards, CRL incorporates additional constraints that represent specific mission requirements or limitations that the agent must comply with during the learning process. In this paper, we address a type of CRL problem where an agent aims to learn the optimal policy to maximize reward while ensuring a desired level of temporal logic constraint satisfaction throughout the learning process. We propose a novel framework that relies on switching between pure learning (reward maximization) and constraint satisfaction. This framework estimates the probability of constraint satisfaction based on earlier trials and properly adjusts the probability of switching between learning and constraint satisfaction policies. We theoretically validate the correctness of the proposed algorithm and demonstrate its performance and scalability through comprehensive simulations.

Reinforcement Learning Under Probabilistic Spatio-Temporal Constraints with Time Windows

We propose an automata-theoretic approach for reinforcement learning (RL) under complex spatio-temporal constraints with time windows. The problem is formulated using a Markov decision process under a bounded temporal logic constraint. Different from existing RL methods that can eventually learn optimal policies satisfying such constraints, our proposed approach enforces a desired probability of constraint satisfaction throughout learning. This is achieved by translating the bounded temporal logic constraint into a total automaton and avoiding "unsafe" actions based on the available prior information regarding the transition probabilities, i.e., a pair of upper and lower bounds for each transition probability. We provide theoretical guarantees on the resulting probability of constraint satisfaction. We also provide numerical results in a scenario where a robot explores the environment to discover high-reward regions while fulfilling some periodic pick-up and delivery tasks that are encoded as temporal logic constraints.

Distributed Planning for Serving Cooperative Tasks with Time Windows: A Game Theoretic Approach

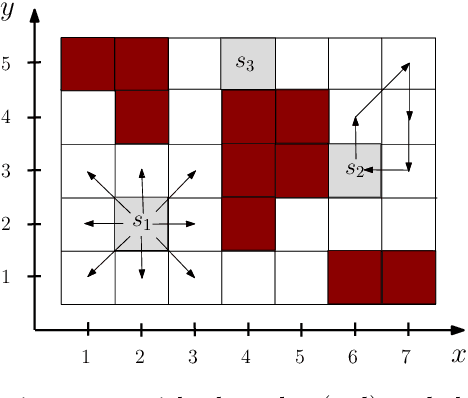
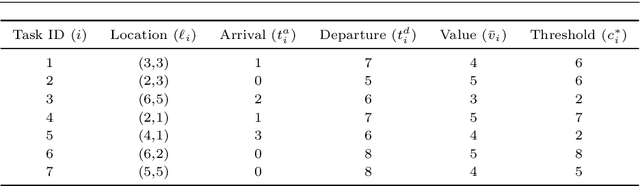
We study distributed planning for multi-robot systems to provide optimal service to cooperative tasks that are distributed over space and time. Each task requires service by sufficiently many robots at the specified location within the specified time window. Tasks arrive over episodes and the robots try to maximize the total value of service in each episode by planning their own trajectories based on the specifications of incoming tasks. Robots are required to start and end each episode at their assigned stations in the environment. We present a game theoretic solution to this problem by mapping it to a game, where the action of each robot is its trajectory in an episode, and using a suitable learning algorithm to obtain optimal joint plans in a distributed manner. We present a systematic way to design minimal action sets (subsets of feasible trajectories) for robots based on the specifications of incoming tasks to facilitate fast learning. We then provide the performance guarantees for the cases where all the robots follow a best response or noisy best response algorithm to iteratively plan their trajectories. While the best response algorithm leads to a Nash equilibrium, the noisy best response algorithm leads to globally optimal joint plans with high probability. We show that the proposed game can in general have arbitrarily poor Nash equilibria, which makes the noisy best response algorithm preferable unless the task specifications are known to have some special structure. We also describe a family of special cases where all the equilibria are guaranteed to have bounded suboptimality. Simulations and experimental results are provided to demonstrate the proposed approach.

Control Synthesis using Signal Temporal Logic Specifications with Integral and Derivative Predicates

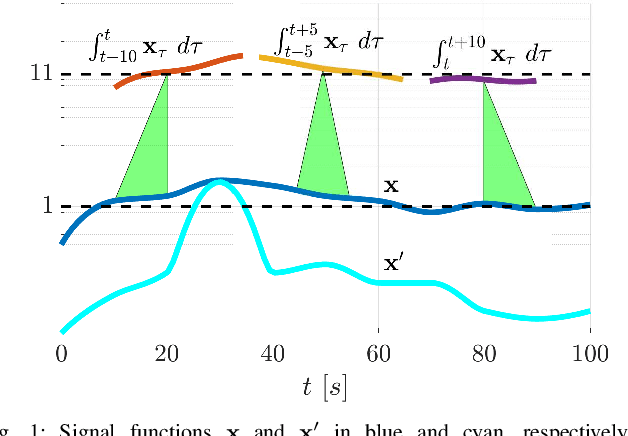
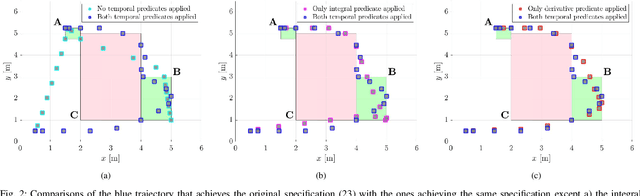
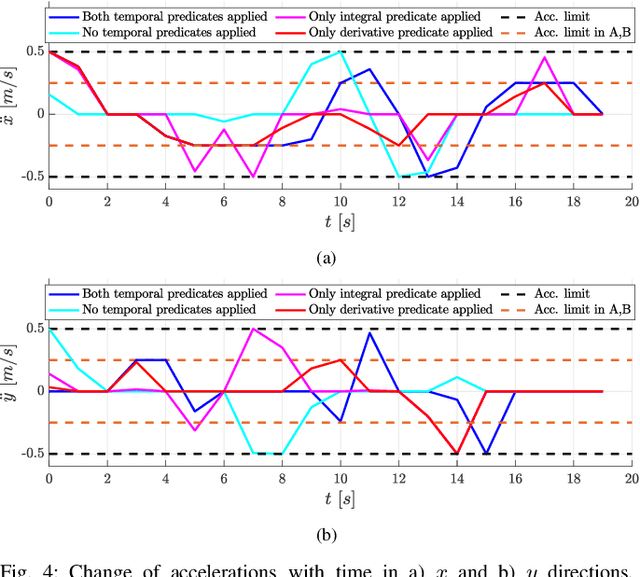
In many applications, the integrals and derivatives of signals carry valuable information (e.g., cumulative success over a time window, the rate of change) regarding the behavior of the underlying system. In this paper, we extend the expressiveness of Signal Temporal Logic (STL) by introducing predicates that can define rich properties related to the integral and derivative of a signal. For control synthesis, the new predicates are encoded into mixed-integer linear inequalities and are used in the formulation of a mixed-integer linear program to find a trajectory that satisfies an STL specification. We discuss the benefits of using the new predicates and illustrate them in a case study showing the influence of the new predicates on the trajectories of an autonomous robot.

Probabilistically Guaranteed Satisfaction of Temporal Logic Constraints During Reinforcement Learning

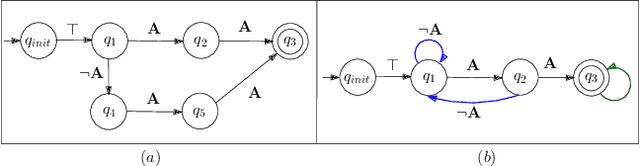
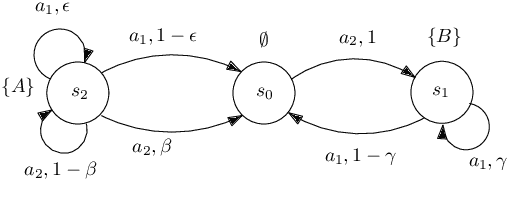
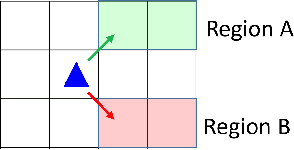
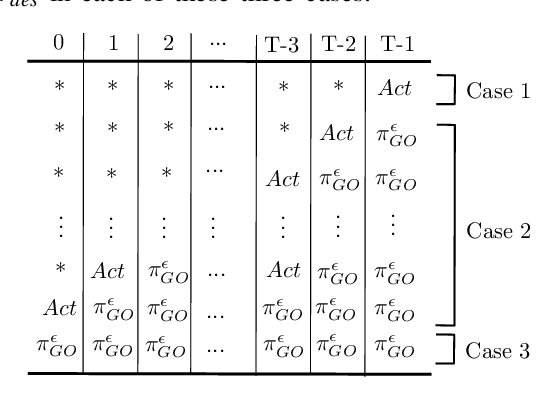
We present a novel reinforcement learning algorithm for finding optimal policies in Markov Decision Processes while satisfying temporal logic constraints with a desired probability throughout the learning process. An automata-theoretic approach is proposed to ensure probabilistic satisfaction of the constraint in each episode, which is different from penalizing violations to achieve constraint satisfaction after a sufficiently large number of episodes. The proposed approach is based on computing a lower bound on the probability of constraint satisfaction and adjusting the exploration behavior as needed. We present theoretical results on the probabilistic constraint satisfaction achieved by the proposed approach. We also numerically demonstrate the proposed idea in a drone scenario, where the constraint is to perform periodically arriving pick-up and delivery tasks and the objective is to fly over high-reward zones to simultaneously perform aerial monitoring.

Decentralized Safe Reactive Planning under TWTL Specifications

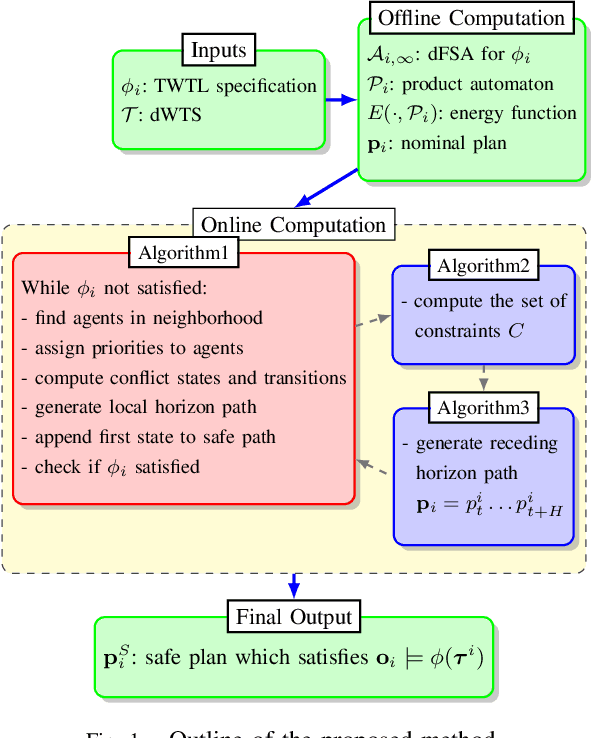
We investigate a multi-agent planning problem, where each agent aims to achieve an individual task while avoiding collisions with others. We assume that each agent's task is expressed as a Time-Window Temporal Logic (TWTL) specification defined over a 3D environment. We propose a decentralized receding horizon algorithm for online planning of trajectories. We show that when the environment is sufficiently connected, the resulting agent trajectories are always safe (collision-free) and lead to the satisfaction of the TWTL specifications or their finite temporal relaxations. Accordingly, deadlocks are always avoided and each agent is guaranteed to safely achieve its task with a finite time-delay in the worst case. Performance of the proposed algorithm is demonstrated via numerical simulations and experiments with quadrotors.

Tractable Reinforcement Learning of Signal Temporal Logic Objectives

Signal temporal logic (STL) is an expressive language to specify time-bound real-world robotic tasks and safety specifications. Recently, there has been an interest in learning optimal policies to satisfy STL specifications via reinforcement learning (RL). Learning to satisfy STL specifications often needs a sufficient length of state history to compute reward and the next action. The need for history results in exponential state-space growth for the learning problem. Thus the learning problem becomes computationally intractable for most real-world applications. In this paper, we propose a compact means to capture state history in a new augmented state-space representation. An approximation to the objective (maximizing probability of satisfaction) is proposed and solved for in the new augmented state-space. We show the performance bound of the approximate solution and compare it with the solution of an existing technique via simulations.

Persistent Surveillance With Energy-Constrained UAVs and Mobile Charging Stations

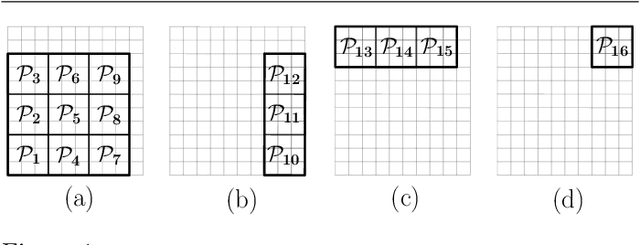
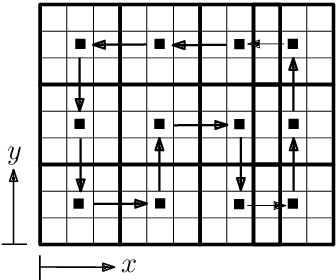
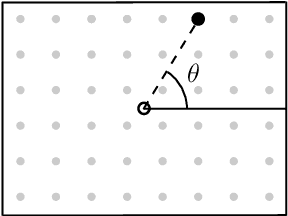
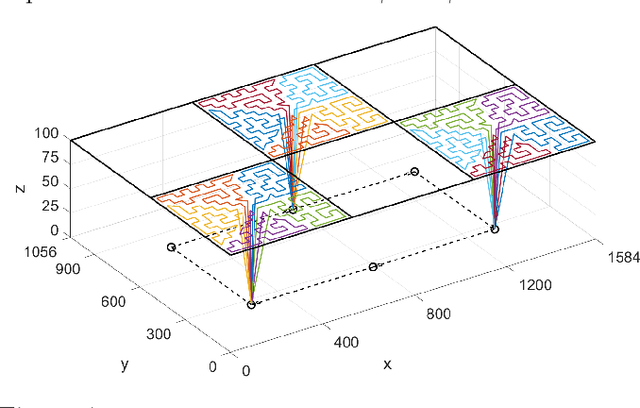
We address the problem of achieving persistent surveillance over an environment by using energy-constrained unmanned aerial vehicles (UAVs), which are supported by unmanned ground vehicles (UGVs) serving as mobile charging stations. Specifically, we plan the trajectories of all vehicles and the charging schedule of UAVs to minimize the long-term maximum age, where age is defined as the time between two consecutive visits to regions of interest in a partitioned environment. We introduce a scalable planning strategy based on 1) creating UAV- UGV teams, 2) decomposing the environment into optimal partitions that can be covered by any of the teams in a single fuel cycle, 3) uniformly distributing the teams over a cyclic path traversing those partitions, and 4) having the UAVs in each team cover their current partition and be transported to the next partition while being recharged by the UGV. We show some results related to the safety and performance of the proposed strategy.

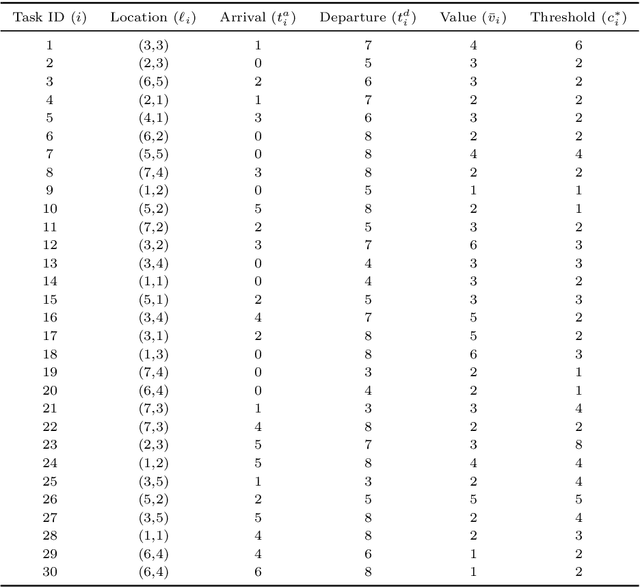
Distributed Path Planning for Executing Cooperative Tasks with Time Windows

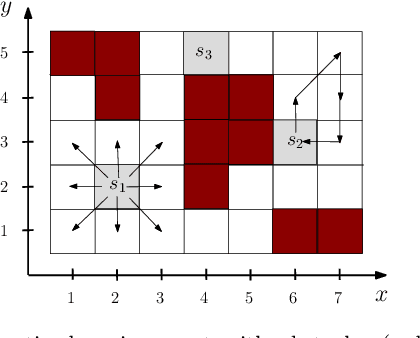
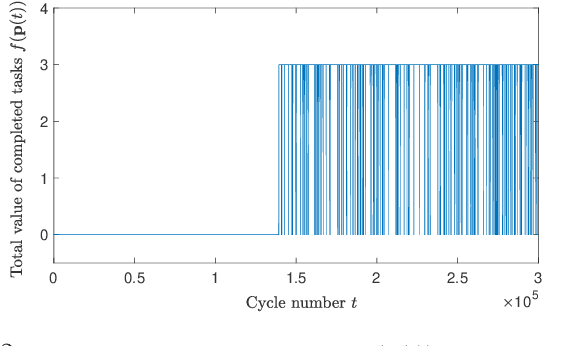
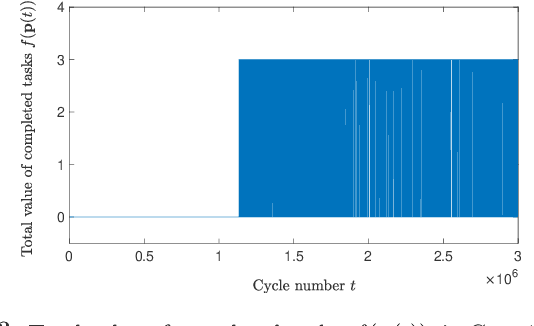
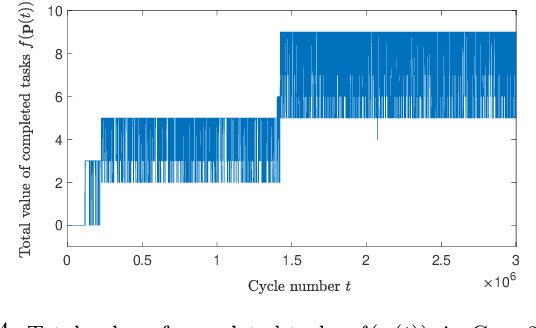
We investigate the distributed planning of robot trajectories for optimal execution of cooperative tasks with time windows. In this setting, each task has a value and is completed if sufficiently many robots are simultaneously present at the necessary location within the specified time window. Tasks keep arriving periodically over cycles. The task specifications (required number of robots, location, time window, and value) are unknown a priori and the robots try to maximize the value of completed tasks by planning their own trajectories for the upcoming cycle based on their past observations in a distributed manner. Considering the recharging and maintenance needs, robots are required to start and end each cycle at their assigned stations located in the environment. We map this problem to a game theoretic formulation and maximize the collective performance through distributed learning. Some simulation results are also provided to demonstrate the performance of the proposed approach.

Robust Satisfaction of Temporal Logic Specifications via Reinforcement Learning

We consider the problem of steering a system with unknown, stochastic dynamics to satisfy a rich, temporally layered task given as a signal temporal logic formula. We represent the system as a Markov decision process in which the states are built from a partition of the state space and the transition probabilities are unknown. We present provably convergent reinforcement learning algorithms to maximize the probability of satisfying a given formula and to maximize the average expected robustness, i.e., a measure of how strongly the formula is satisfied. We demonstrate via a pair of robot navigation simulation case studies that reinforcement learning with robustness maximization performs better than probability maximization in terms of both probability of satisfaction and expected robustness.