Probabilistic Satisfaction of Temporal Logic Constraints in Reinforcement Learning via Adaptive Policy-Switching

Constrained Reinforcement Learning (CRL) is a subset of machine learning that introduces constraints into the traditional reinforcement learning (RL) framework. Unlike conventional RL which aims solely to maximize cumulative rewards, CRL incorporates additional constraints that represent specific mission requirements or limitations that the agent must comply with during the learning process. In this paper, we address a type of CRL problem where an agent aims to learn the optimal policy to maximize reward while ensuring a desired level of temporal logic constraint satisfaction throughout the learning process. We propose a novel framework that relies on switching between pure learning (reward maximization) and constraint satisfaction. This framework estimates the probability of constraint satisfaction based on earlier trials and properly adjusts the probability of switching between learning and constraint satisfaction policies. We theoretically validate the correctness of the proposed algorithm and demonstrate its performance and scalability through comprehensive simulations.

Control Synthesis using Signal Temporal Logic Specifications with Integral and Derivative Predicates

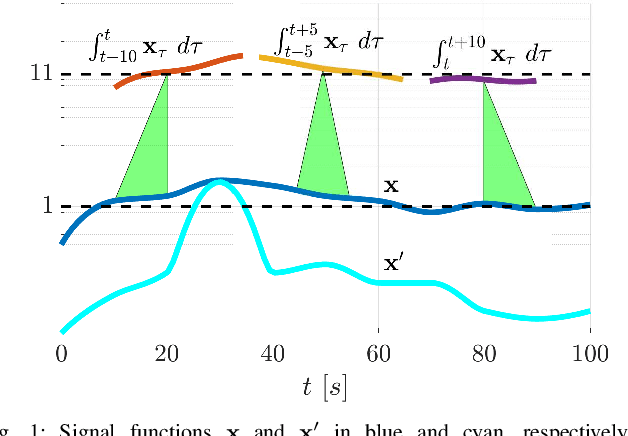
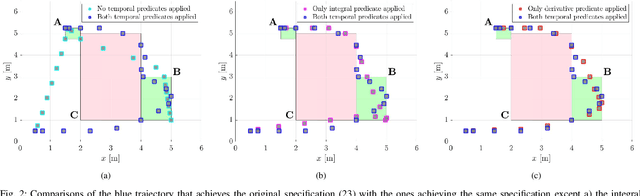
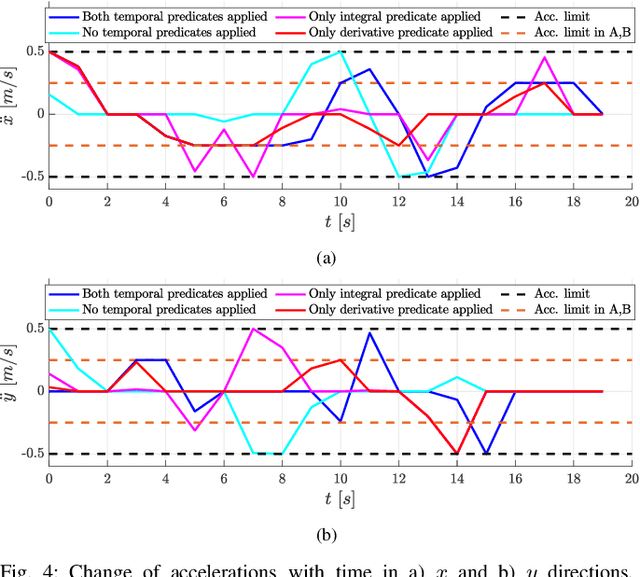
In many applications, the integrals and derivatives of signals carry valuable information (e.g., cumulative success over a time window, the rate of change) regarding the behavior of the underlying system. In this paper, we extend the expressiveness of Signal Temporal Logic (STL) by introducing predicates that can define rich properties related to the integral and derivative of a signal. For control synthesis, the new predicates are encoded into mixed-integer linear inequalities and are used in the formulation of a mixed-integer linear program to find a trajectory that satisfies an STL specification. We discuss the benefits of using the new predicates and illustrate them in a case study showing the influence of the new predicates on the trajectories of an autonomous robot.