Fast Decomposition of Temporal Logic Specifications for Heterogeneous Teams

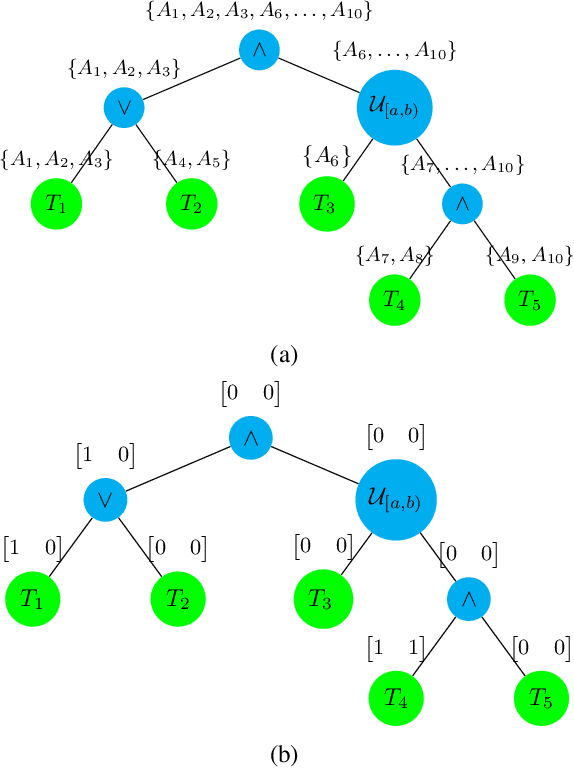
In this work, we focus on decomposing large multi-agent path planning problems with global temporal logic goals (common to all agents) into smaller sub-problems that can be solved and executed independently. Crucially, the sub-problems' solutions must jointly satisfy the common global mission specification. The agents' missions are given as Capability Temporal Logic (CaTL) formulas, a fragment of signal temporal logic, that can express properties over tasks involving multiple agent capabilities (sensors, e.g., camera, IR, and effectors, e.g., wheeled, flying, manipulators) under strict timing constraints. The approach we take is to decompose both the temporal logic specification and the team of agents. We jointly reason about the assignment of agents to subteams and the decomposition of formulas using a satisfiability modulo theories (SMT) approach. The output of the SMT is then distributed to subteams and leads to a significant speed up in planning time. We include computational results to evaluate the efficiency of our solution, as well as the trade-offs introduced by the conservative nature of the SMT encoding.

Robust Satisfaction of Temporal Logic Specifications via Reinforcement Learning

We consider the problem of steering a system with unknown, stochastic dynamics to satisfy a rich, temporally layered task given as a signal temporal logic formula. We represent the system as a Markov decision process in which the states are built from a partition of the state space and the transition probabilities are unknown. We present provably convergent reinforcement learning algorithms to maximize the probability of satisfying a given formula and to maximize the average expected robustness, i.e., a measure of how strongly the formula is satisfied. We demonstrate via a pair of robot navigation simulation case studies that reinforcement learning with robustness maximization performs better than probability maximization in terms of both probability of satisfaction and expected robustness.

Technical Report: Distribution Temporal Logic: Combining Correctness with Quality of Estimation

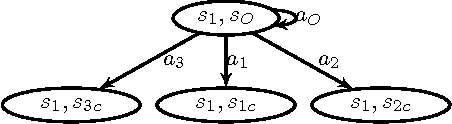
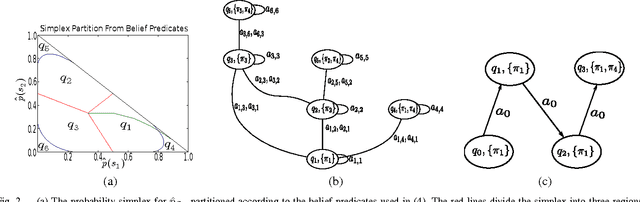
We present a new temporal logic called Distribution Temporal Logic (DTL) defined over predicates of belief states and hidden states of partially observable systems. DTL can express properties involving uncertainty and likelihood that cannot be described by existing logics. A co-safe formulation of DTL is defined and algorithmic procedures are given for monitoring executions of a partially observable Markov decision process with respect to such formulae. A simulation case study of a rescue robotics application outlines our approach.

Technical Report: A Receding Horizon Algorithm for Informative Path Planning with Temporal Logic Constraints

This technical report is an extended version of the paper 'A Receding Horizon Algorithm for Informative Path Planning with Temporal Logic Constraints' accepted to the 2013 IEEE International Conference on Robotics and Automation (ICRA). This paper considers the problem of finding the most informative path for a sensing robot under temporal logic constraints, a richer set of constraints than have previously been considered in information gathering. An algorithm for informative path planning is presented that leverages tools from information theory and formal control synthesis, and is proven to give a path that satisfies the given temporal logic constraints. The algorithm uses a receding horizon approach in order to provide a reactive, on-line solution while mitigating computational complexity. Statistics compiled from multiple simulation studies indicate that this algorithm performs better than a baseline exhaustive search approach.