Distributed Planning for Serving Cooperative Tasks with Time Windows: A Game Theoretic Approach
Paper and Code
Jul 18, 2021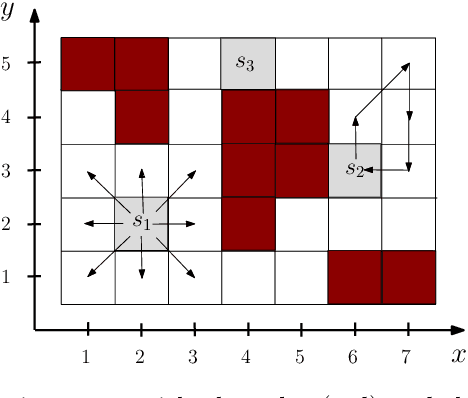
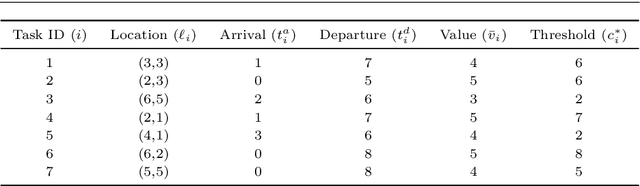
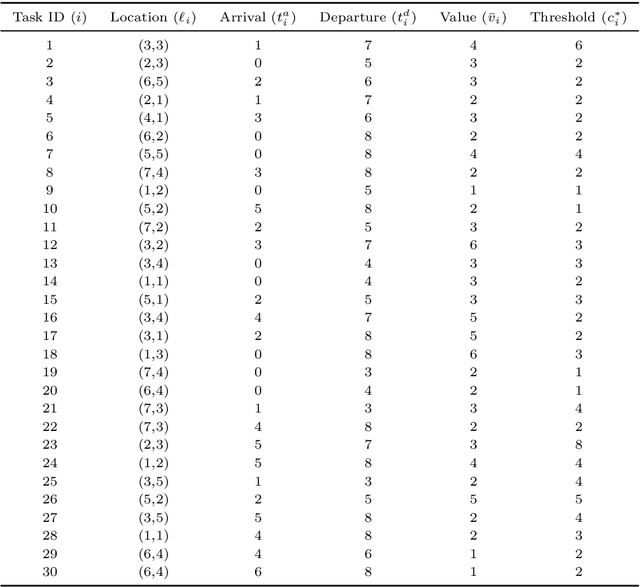
We study distributed planning for multi-robot systems to provide optimal service to cooperative tasks that are distributed over space and time. Each task requires service by sufficiently many robots at the specified location within the specified time window. Tasks arrive over episodes and the robots try to maximize the total value of service in each episode by planning their own trajectories based on the specifications of incoming tasks. Robots are required to start and end each episode at their assigned stations in the environment. We present a game theoretic solution to this problem by mapping it to a game, where the action of each robot is its trajectory in an episode, and using a suitable learning algorithm to obtain optimal joint plans in a distributed manner. We present a systematic way to design minimal action sets (subsets of feasible trajectories) for robots based on the specifications of incoming tasks to facilitate fast learning. We then provide the performance guarantees for the cases where all the robots follow a best response or noisy best response algorithm to iteratively plan their trajectories. While the best response algorithm leads to a Nash equilibrium, the noisy best response algorithm leads to globally optimal joint plans with high probability. We show that the proposed game can in general have arbitrarily poor Nash equilibria, which makes the noisy best response algorithm preferable unless the task specifications are known to have some special structure. We also describe a family of special cases where all the equilibria are guaranteed to have bounded suboptimality. Simulations and experimental results are provided to demonstrate the proposed approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge