Photonic Accelerators for Image Segmentation in Autonomous Driving and Defect Detection

Photonic computing promises faster and more energy-efficient deep neural network (DNN) inference than traditional digital hardware. Advances in photonic computing can have profound impacts on applications such as autonomous driving and defect detection that depend on fast, accurate and energy efficient execution of image segmentation models. In this paper, we investigate image segmentation on photonic accelerators to explore: a) the types of image segmentation DNN architectures that are best suited for photonic accelerators, and b) the throughput and energy efficiency of executing the different image segmentation models on photonic accelerators, along with the trade-offs involved therein. Specifically, we demonstrate that certain segmentation models exhibit negligible loss in accuracy (compared to digital float32 models) when executed on photonic accelerators, and explore the empirical reasoning for their robustness. We also discuss techniques for recovering accuracy in the case of models that do not perform well. Further, we compare throughput (inferences-per-second) and energy consumption estimates for different image segmentation workloads on photonic accelerators. We discuss the challenges and potential optimizations that can help improve the application of photonic accelerators to such computer vision tasks.

Adaptive Block Floating-Point for Analog Deep Learning Hardware

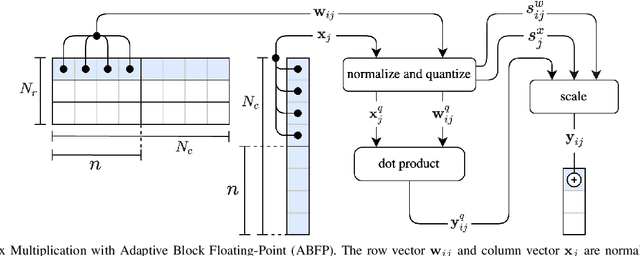
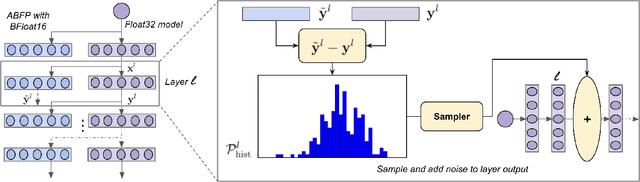
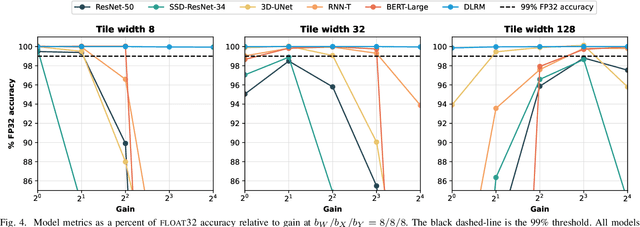
Analog mixed-signal (AMS) devices promise faster, more energy-efficient deep neural network (DNN) inference than their digital counterparts. However, recent studies show that DNNs on AMS devices with fixed-point numbers can incur an accuracy penalty because of precision loss. To mitigate this penalty, we present a novel AMS-compatible adaptive block floating-point (ABFP) number representation. We also introduce amplification (or gain) as a method for increasing the accuracy of the number representation without increasing the bit precision of the output. We evaluate the effectiveness of ABFP on the DNNs in the MLPerf datacenter inference benchmark -- realizing less than $1\%$ loss in accuracy compared to FLOAT32. We also propose a novel method of finetuning for AMS devices, Differential Noise Finetuning (DNF), which samples device noise to speed up finetuning compared to conventional Quantization-Aware Training.

Latent Space Simulation for Carbon Capture Design Optimization

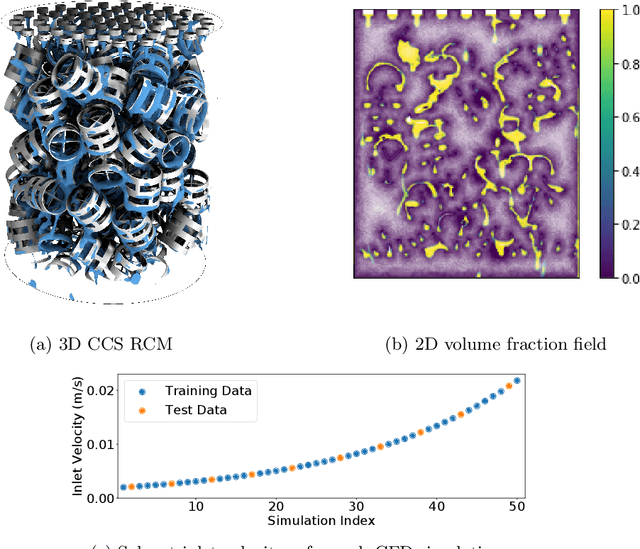
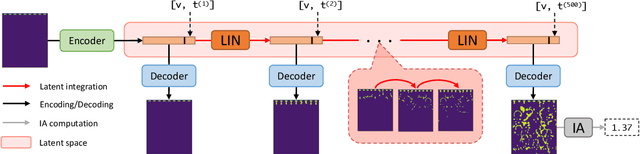
The CO2 capture efficiency in solvent-based carbon capture systems (CCSs) critically depends on the gas-solvent interfacial area (IA), making maximization of IA a foundational challenge in CCS design. While the IA associated with a particular CCS design can be estimated via a computational fluid dynamics (CFD) simulation, using CFD to derive the IAs associated with numerous CCS designs is prohibitively costly. Fortunately, previous works such as Deep Fluids (DF) (Kim et al., 2019) show that large simulation speedups are achievable by replacing CFD simulators with neural network (NN) surrogates that faithfully mimic the CFD simulation process. This raises the possibility of a fast, accurate replacement for a CFD simulator and therefore efficient approximation of the IAs required by CCS design optimization. Thus, here, we build on the DF approach to develop surrogates that can successfully be applied to our complex carbon-capture CFD simulations. Our optimized DF-style surrogates produce large speedups (4000x) while obtaining IA relative errors as low as 4% on unseen CCS configurations that lie within the range of training configurations. This hints at the promise of NN surrogates for our CCS design optimization problem. Nonetheless, DF has inherent limitations with respect to CCS design (e.g., limited transferability of trained models to new CCS packings). We conclude with ideas to address these challenges.

Efficient nonlinear manifold reduced order model

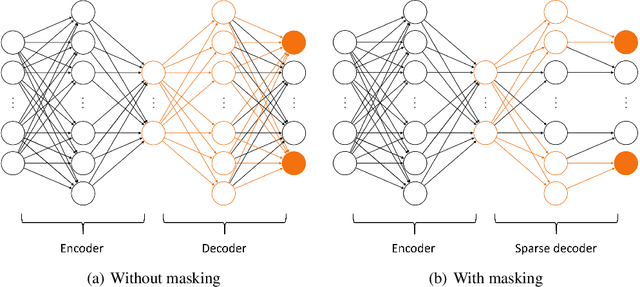
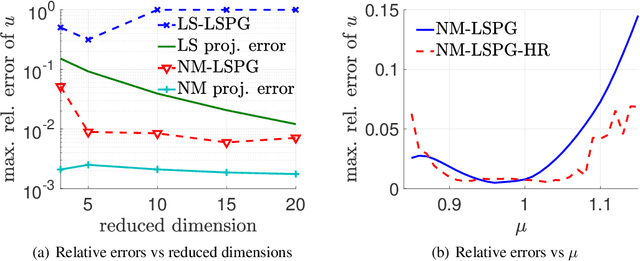
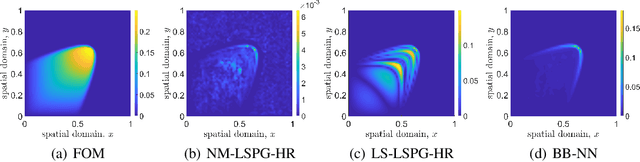
Traditional linear subspace reduced order models (LS-ROMs) are able to accelerate physical simulations, in which the intrinsic solution space falls into a subspace with a small dimension, i.e., the solution space has a small Kolmogorov n-width. However, for physical phenomena not of this type, such as advection-dominated flow phenomena, a low-dimensional linear subspace poorly approximates the solution. To address cases such as these, we have developed an efficient nonlinear manifold ROM (NM-ROM), which can better approximate high-fidelity model solutions with a smaller latent space dimension than the LS-ROMs. Our method takes advantage of the existing numerical methods that are used to solve the corresponding full order models (FOMs). The efficiency is achieved by developing a hyper-reduction technique in the context of the NM-ROM. Numerical results show that neural networks can learn a more efficient latent space representation on advection-dominated data from 2D Burgers' equations with a high Reynolds number. A speed-up of up to 11.7 for 2D Burgers' equations is achieved with an appropriate treatment of the nonlinear terms through a hyper-reduction technique.

A fast and accurate physics-informed neural network reduced order model with shallow masked autoencoder

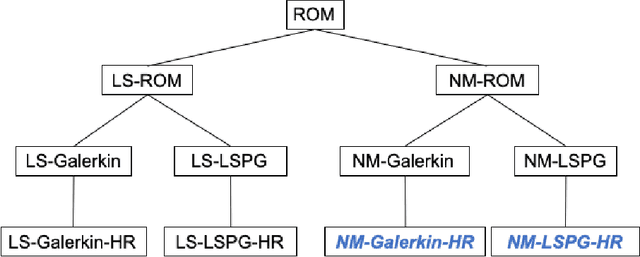
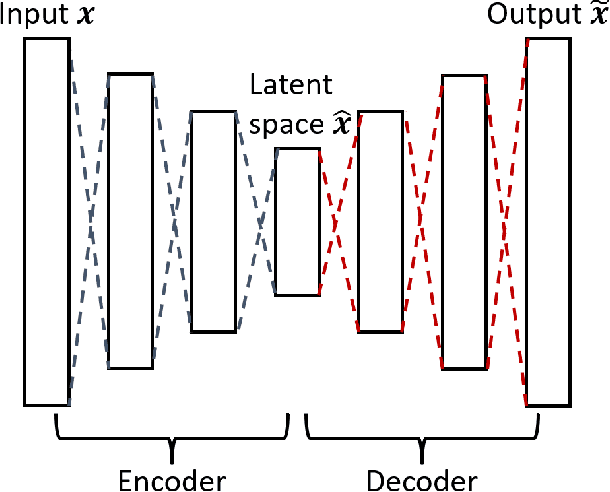
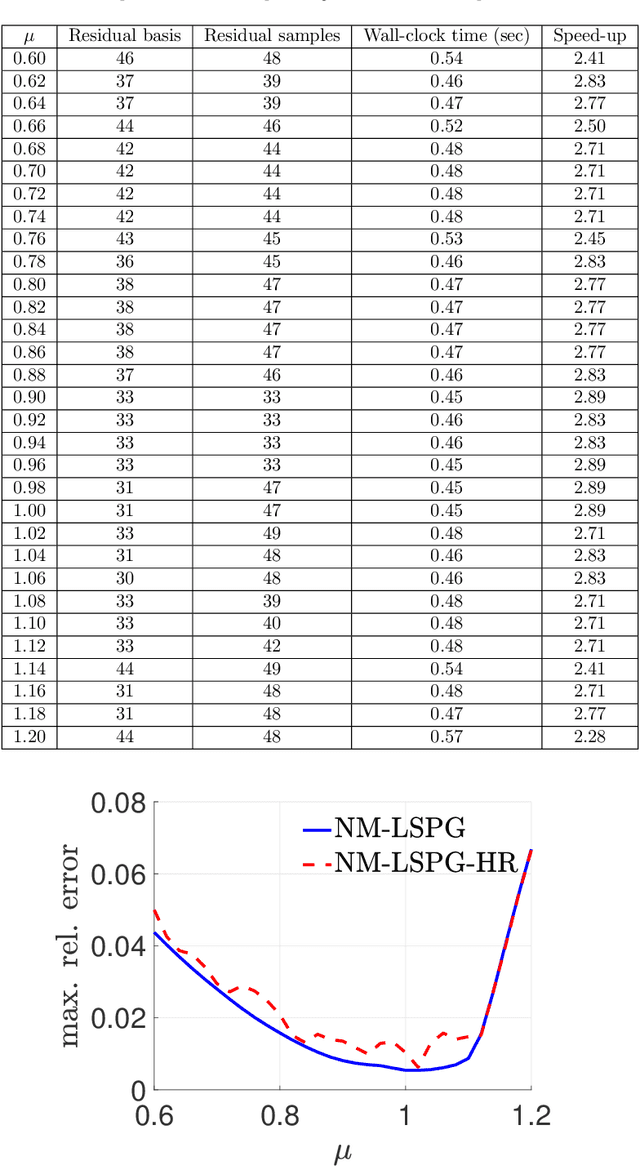
Traditional linear subspace reduced order models (LS-ROMs) are able to accelerate physical simulations, in which the intrinsic solution space falls into a subspace with a small dimension, i.e., the solution space has a small Kolmogorov n-width. However, for physical phenomena not of this type, e.g., any advection-dominated flow phenomena, such as in traffic flow, atmospheric flows, and air flow over vehicles, a low-dimensional linear subspace poorly approximates the solution. To address cases such as these, we have developed a fast and accurate physics-informed neural network ROM, namely nonlinear manifold ROM (NM-ROM), which can better approximate high-fidelity model solutions with a smaller latent space dimension than the LS-ROMs. Our method takes advantage of the existing numerical methods that are used to solve the corresponding full order models. The efficiency is achieved by developing a hyper-reduction technique in the context of the NM-ROM. Numerical results show that neural networks can learn a more efficient latent space representation on advection-dominated data from 1D and 2D Burgers' equations. A speedup of up to 2.6 for 1D Burgers' and a speedup of 11.7 for 2D Burgers' equations are achieved with an appropriate treatment of the nonlinear terms through a hyper-reduction technique. Finally, a posteriori error bounds for the NM-ROMs are derived that take account of the hyper-reduced operators.