Bayesian Optimization of Antibodies Informed by a Generative Model of Evolving Sequences

To build effective therapeutics, biologists iteratively mutate antibody sequences to improve binding and stability. Proposed mutations can be informed by previous measurements or by learning from large antibody databases to predict only typical antibodies. Unfortunately, the space of typical antibodies is enormous to search, and experiments often fail to find suitable antibodies on a budget. We introduce Clone-informed Bayesian Optimization (CloneBO), a Bayesian optimization procedure that efficiently optimizes antibodies in the lab by teaching a generative model how our immune system optimizes antibodies. Our immune system makes antibodies by iteratively evolving specific portions of their sequences to bind their target strongly and stably, resulting in a set of related, evolving sequences known as a clonal family. We train a large language model, CloneLM, on hundreds of thousands of clonal families and use it to design sequences with mutations that are most likely to optimize an antibody within the human immune system. We propose to guide our designs to fit previous measurements with a twisted sequential Monte Carlo procedure. We show that CloneBO optimizes antibodies substantially more efficiently than previous methods in realistic in silico experiments and designs stronger and more stable binders in in vitro wet lab experiments.

Unmasking Trees for Tabular Data

We herein describe UnmaskingTrees, a method and open-source software package for tabular data generation and, especially, imputation. Our experiments suggest that training gradient-boosted trees to incrementally unmask features offers a simple, strong baseline for imputation.

How Lexical is Bilingual Lexicon Induction?

In contemporary machine learning approaches to bilingual lexicon induction (BLI), a model learns a mapping between the embedding spaces of a language pair. Recently, retrieve-and-rank approach to BLI has achieved state of the art results on the task. However, the problem remains challenging in low-resource settings, due to the paucity of data. The task is complicated by factors such as lexical variation across languages. We argue that the incorporation of additional lexical information into the recent retrieve-and-rank approach should improve lexicon induction. We demonstrate the efficacy of our proposed approach on XLING, improving over the previous state of the art by an average of 2\% across all language pairs.

Inverse distance weighting attention

We report the effects of replacing the scaled dot-product (within softmax) attention with the negative-log of Euclidean distance. This form of attention simplifies to inverse distance weighting interpolation. Used in simple one hidden layer networks and trained with vanilla cross-entropy loss on classification problems, it tends to produce a key matrix containing prototypes and a value matrix with corresponding logits. We also show that the resulting interpretable networks can be augmented with manually-constructed prototypes to perform low-impact handling of special cases.

The Kernel Density Integral Transformation

Feature preprocessing continues to play a critical role when applying machine learning and statistical methods to tabular data. In this paper, we propose the use of the kernel density integral transformation as a feature preprocessing step. Our approach subsumes the two leading feature preprocessing methods as limiting cases: linear min-max scaling and quantile transformation. We demonstrate that, without hyperparameter tuning, the kernel density integral transformation can be used as a simple drop-in replacement for either method, offering robustness to the weaknesses of each. Alternatively, with tuning of a single continuous hyperparameter, we frequently outperform both of these methods. Finally, we show that the kernel density transformation can be profitably applied to statistical data analysis, particularly in correlation analysis and univariate clustering.

Look-ups are not all you need for deep learning inference

Fast approximations to matrix multiplication have the potential to dramatically reduce the cost of neural network inference. Recent work on approximate matrix multiplication proposed to replace costly multiplications with table-lookups by fitting a fast hash function from training data. In this work, we propose improvements to this previous work, targeted to the deep learning inference setting, where one has access to both training data and fixed (already learned) model weight matrices. We further propose a fine-tuning procedure for accelerating entire neural networks while minimizing loss in accuracy. Finally, we analyze the proposed method on a simple image classification task. While we show improvements to prior work, overall classification accuracy remains substantially diminished compared to exact matrix multiplication. Our work, despite this negative result, points the way towards future efforts to accelerate inner products with fast nonlinear hashing methods.

Adaptive Block Floating-Point for Analog Deep Learning Hardware

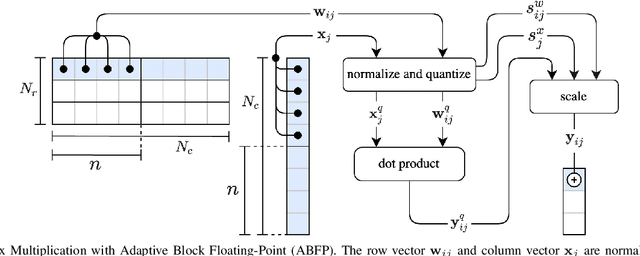
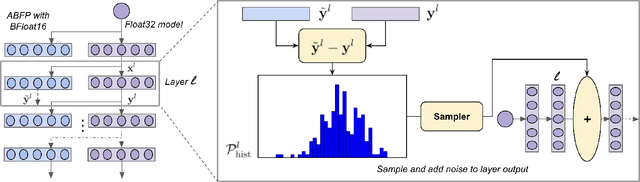
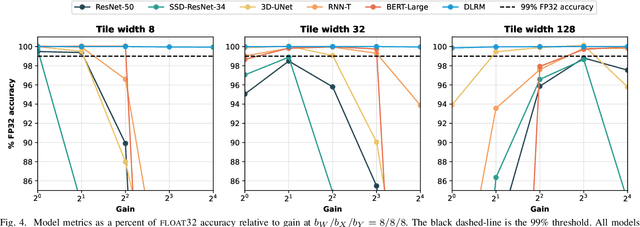
Analog mixed-signal (AMS) devices promise faster, more energy-efficient deep neural network (DNN) inference than their digital counterparts. However, recent studies show that DNNs on AMS devices with fixed-point numbers can incur an accuracy penalty because of precision loss. To mitigate this penalty, we present a novel AMS-compatible adaptive block floating-point (ABFP) number representation. We also introduce amplification (or gain) as a method for increasing the accuracy of the number representation without increasing the bit precision of the output. We evaluate the effectiveness of ABFP on the DNNs in the MLPerf datacenter inference benchmark -- realizing less than $1\%$ loss in accuracy compared to FLOAT32. We also propose a novel method of finetuning for AMS devices, Differential Noise Finetuning (DNF), which samples device noise to speed up finetuning compared to conventional Quantization-Aware Training.

Towards Backwards-Compatible Data with Confounded Domain Adaptation

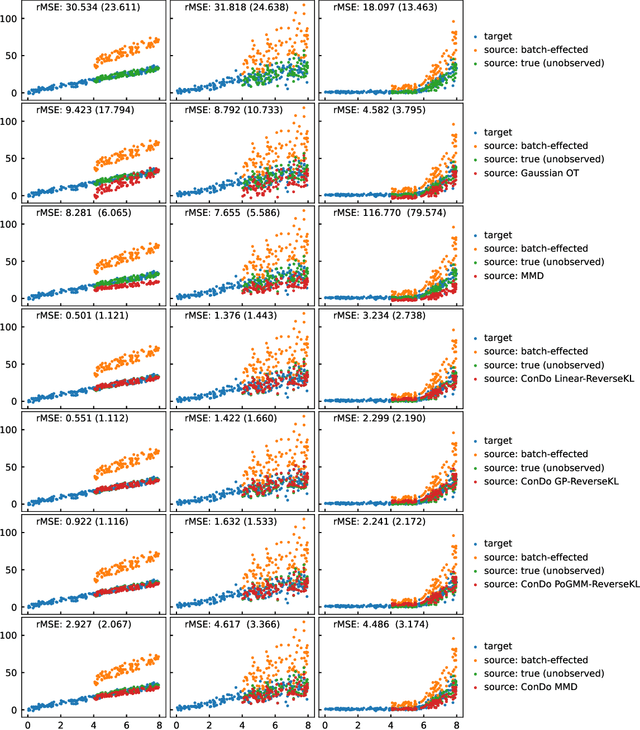
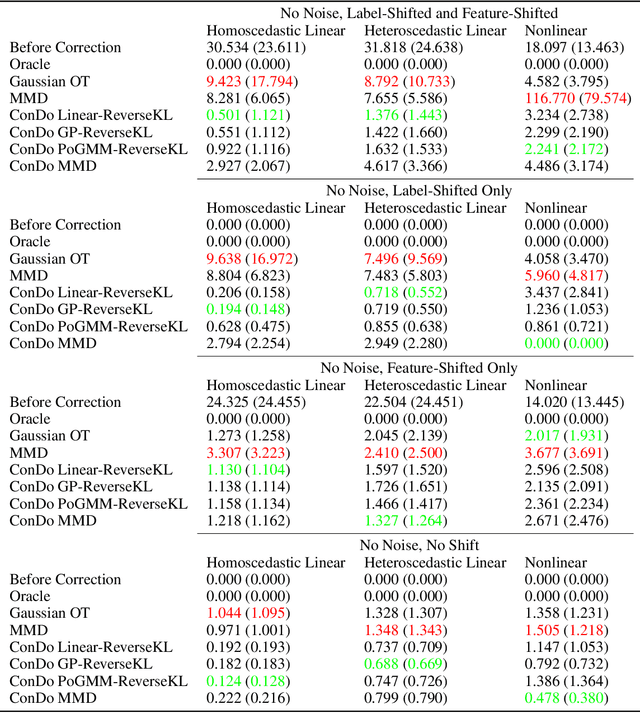
Most current domain adaptation methods address either covariate shift or label shift, but are not applicable where they occur simultaneously and are confounded with each other. Domain adaptation approaches which do account for such confounding are designed to adapt covariates to optimally predict a particular label whose shift is confounded with covariate shift. In this paper, we instead seek to achieve general-purpose data backwards compatibility. This would allow the adapted covariates to be used for a variety of downstream problems, including on pre-existing prediction models and on data analytics tasks. To do this we consider a special case of generalized label shift (GLS), which we call confounded shift. We present a novel framework for this problem, based on minimizing the expected divergence between the source and target conditional distributions, conditioning on possible confounders. Within this framework, we propose using the reverse Kullback-Leibler divergence, demonstrating the use of parametric and nonparametric Gaussian estimators of the conditional distribution. We also propose using the Maximum Mean Discrepancy (MMD), introducing a dynamic strategy for choosing the kernel bandwidth, which is applicable even outside the confounded shift setting. Finally, we demonstrate our approach on synthetic and real datasets.

Large-Scale Optimization Algorithms for Sparse Conditional Gaussian Graphical Models

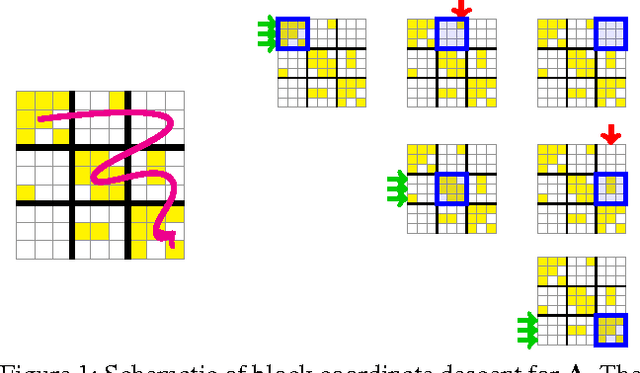
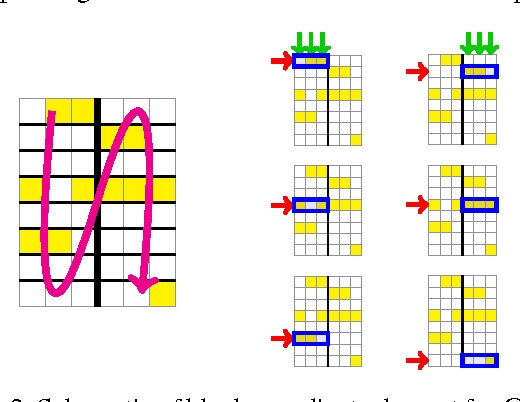
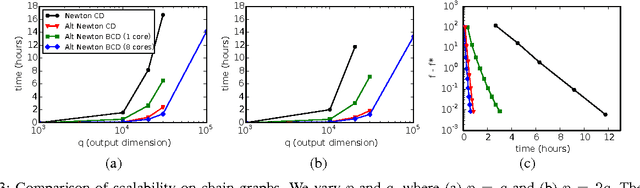
This paper addresses the problem of scalable optimization for L1-regularized conditional Gaussian graphical models. Conditional Gaussian graphical models generalize the well-known Gaussian graphical models to conditional distributions to model the output network influenced by conditioning input variables. While highly scalable optimization methods exist for sparse Gaussian graphical model estimation, state-of-the-art methods for conditional Gaussian graphical models are not efficient enough and more importantly, fail due to memory constraints for very large problems. In this paper, we propose a new optimization procedure based on a Newton method that efficiently iterates over two sub-problems, leading to drastic improvement in computation time compared to the previous methods. We then extend our method to scale to large problems under memory constraints, using block coordinate descent to limit memory usage while achieving fast convergence. Using synthetic and genomic data, we show that our methods can solve one million dimensional problems to high accuracy in a little over a day on a single machine.