Bayesian Optimization of Antibodies Informed by a Generative Model of Evolving Sequences

To build effective therapeutics, biologists iteratively mutate antibody sequences to improve binding and stability. Proposed mutations can be informed by previous measurements or by learning from large antibody databases to predict only typical antibodies. Unfortunately, the space of typical antibodies is enormous to search, and experiments often fail to find suitable antibodies on a budget. We introduce Clone-informed Bayesian Optimization (CloneBO), a Bayesian optimization procedure that efficiently optimizes antibodies in the lab by teaching a generative model how our immune system optimizes antibodies. Our immune system makes antibodies by iteratively evolving specific portions of their sequences to bind their target strongly and stably, resulting in a set of related, evolving sequences known as a clonal family. We train a large language model, CloneLM, on hundreds of thousands of clonal families and use it to design sequences with mutations that are most likely to optimize an antibody within the human immune system. We propose to guide our designs to fit previous measurements with a twisted sequential Monte Carlo procedure. We show that CloneBO optimizes antibodies substantially more efficiently than previous methods in realistic in silico experiments and designs stronger and more stable binders in in vitro wet lab experiments.

Scalable and Flexible Causal Discovery with an Efficient Test for Adjacency

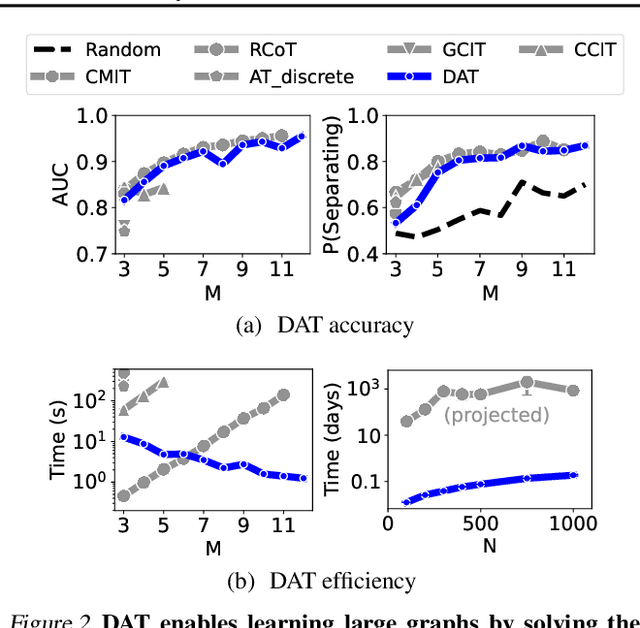
To make accurate predictions, understand mechanisms, and design interventions in systems of many variables, we wish to learn causal graphs from large scale data. Unfortunately the space of all possible causal graphs is enormous so scalably and accurately searching for the best fit to the data is a challenge. In principle we could substantially decrease the search space, or learn the graph entirely, by testing the conditional independence of variables. However, deciding if two variables are adjacent in a causal graph may require an exponential number of tests. Here we build a scalable and flexible method to evaluate if two variables are adjacent in a causal graph, the Differentiable Adjacency Test (DAT). DAT replaces an exponential number of tests with a provably equivalent relaxed problem. It then solves this problem by training two neural networks. We build a graph learning method based on DAT, DAT-Graph, that can also learn from data with interventions. DAT-Graph can learn graphs of 1000 variables with state of the art accuracy. Using the graph learned by DAT-Graph, we also build models that make much more accurate predictions of the effects of interventions on large scale RNA sequencing data.

Biological Sequence Kernels with Guaranteed Flexibility

Applying machine learning to biological sequences - DNA, RNA and protein - has enormous potential to advance human health, environmental sustainability, and fundamental biological understanding. However, many existing machine learning methods are ineffective or unreliable in this problem domain. We study these challenges theoretically, through the lens of kernels. Methods based on kernels are ubiquitous: they are used to predict molecular phenotypes, design novel proteins, compare sequence distributions, and more. Many methods that do not use kernels explicitly still rely on them implicitly, including a wide variety of both deep learning and physics-based techniques. While kernels for other types of data are well-studied theoretically, the structure of biological sequence space (discrete, variable length sequences), as well as biological notions of sequence similarity, present unique mathematical challenges. We formally analyze how well kernels for biological sequences can approximate arbitrary functions on sequence space and how well they can distinguish different sequence distributions. In particular, we establish conditions under which biological sequence kernels are universal, characteristic and metrize the space of distributions. We show that a large number of existing kernel-based machine learning methods for biological sequences fail to meet our conditions and can as a consequence fail severely. We develop straightforward and computationally tractable ways of modifying existing kernels to satisfy our conditions, imbuing them with strong guarantees on accuracy and reliability. Our proof techniques build on and extend the theory of kernels with discrete masses. We illustrate our theoretical results in simulation and on real biological data sets.