Efficient nonlinear manifold reduced order model
Paper and Code
Nov 13, 2020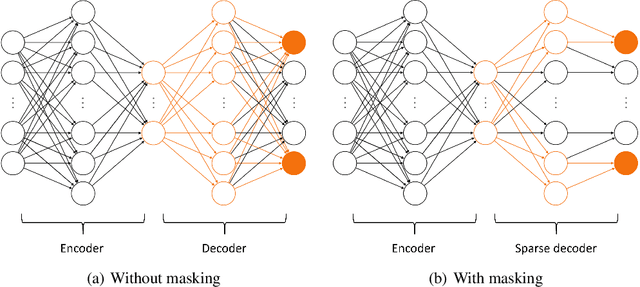

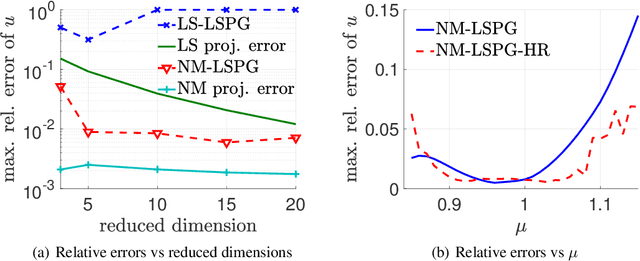
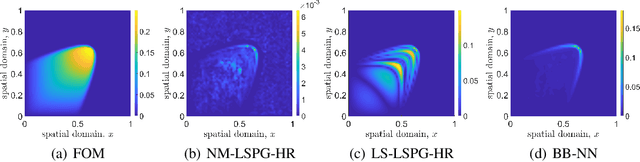
Traditional linear subspace reduced order models (LS-ROMs) are able to accelerate physical simulations, in which the intrinsic solution space falls into a subspace with a small dimension, i.e., the solution space has a small Kolmogorov n-width. However, for physical phenomena not of this type, such as advection-dominated flow phenomena, a low-dimensional linear subspace poorly approximates the solution. To address cases such as these, we have developed an efficient nonlinear manifold ROM (NM-ROM), which can better approximate high-fidelity model solutions with a smaller latent space dimension than the LS-ROMs. Our method takes advantage of the existing numerical methods that are used to solve the corresponding full order models (FOMs). The efficiency is achieved by developing a hyper-reduction technique in the context of the NM-ROM. Numerical results show that neural networks can learn a more efficient latent space representation on advection-dominated data from 2D Burgers' equations with a high Reynolds number. A speed-up of up to 11.7 for 2D Burgers' equations is achieved with an appropriate treatment of the nonlinear terms through a hyper-reduction technique.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge