A fast and accurate physics-informed neural network reduced order model with shallow masked autoencoder
Paper and Code
Sep 28, 2020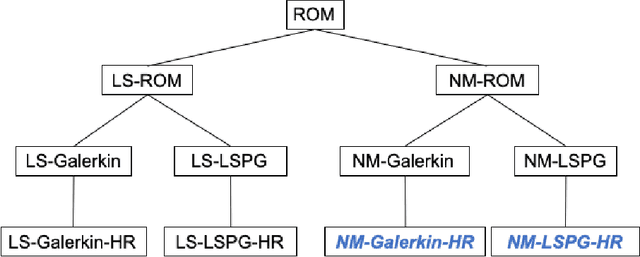

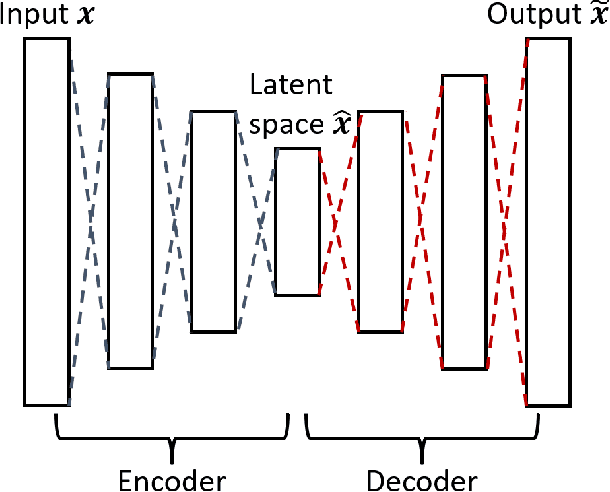
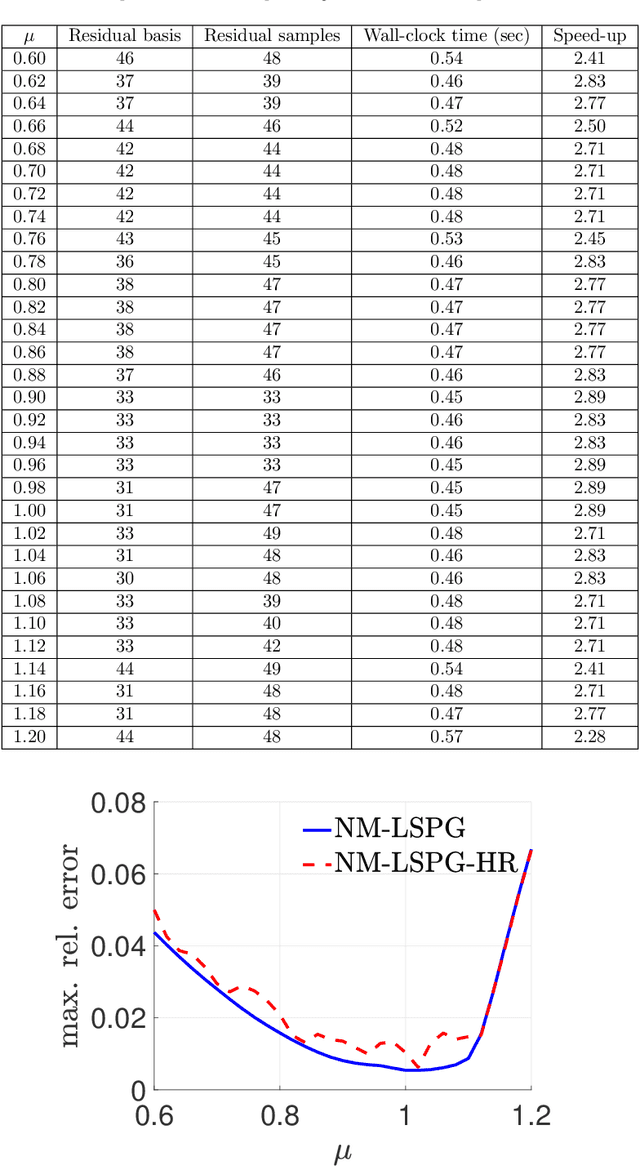
Traditional linear subspace reduced order models (LS-ROMs) are able to accelerate physical simulations, in which the intrinsic solution space falls into a subspace with a small dimension, i.e., the solution space has a small Kolmogorov n-width. However, for physical phenomena not of this type, e.g., any advection-dominated flow phenomena, such as in traffic flow, atmospheric flows, and air flow over vehicles, a low-dimensional linear subspace poorly approximates the solution. To address cases such as these, we have developed a fast and accurate physics-informed neural network ROM, namely nonlinear manifold ROM (NM-ROM), which can better approximate high-fidelity model solutions with a smaller latent space dimension than the LS-ROMs. Our method takes advantage of the existing numerical methods that are used to solve the corresponding full order models. The efficiency is achieved by developing a hyper-reduction technique in the context of the NM-ROM. Numerical results show that neural networks can learn a more efficient latent space representation on advection-dominated data from 1D and 2D Burgers' equations. A speedup of up to 2.6 for 1D Burgers' and a speedup of 11.7 for 2D Burgers' equations are achieved with an appropriate treatment of the nonlinear terms through a hyper-reduction technique. Finally, a posteriori error bounds for the NM-ROMs are derived that take account of the hyper-reduced operators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge