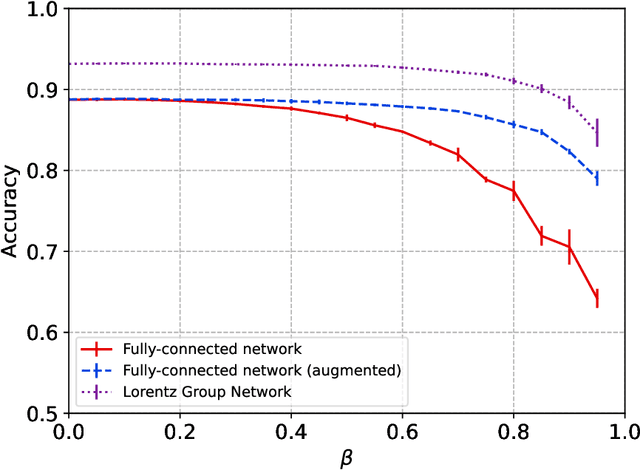
Equivariance Is Not All You Need: Characterizing the Utility of Equivariant Graph Neural Networks for Particle Physics Tasks

Incorporating inductive biases into ML models is an active area of ML research, especially when ML models are applied to data about the physical world. Equivariant Graph Neural Networks (GNNs) have recently become a popular method for learning from physics data because they directly incorporate the symmetries of the underlying physical system. Drawing from the relevant literature around group equivariant networks, this paper presents a comprehensive evaluation of the proposed benefits of equivariant GNNs by using real-world particle physics reconstruction tasks as an evaluation test-bed. We demonstrate that many of the theoretical benefits generally associated with equivariant networks may not hold for realistic systems and introduce compelling directions for future research that will benefit both the scientific theory of ML and physics applications.

Graph Structure from Point Clouds: Geometric Attention is All You Need

The use of graph neural networks has produced significant advances in point cloud problems, such as those found in high energy physics. The question of how to produce a graph structure in these problems is usually treated as a matter of heuristics, employing fully connected graphs or K-nearest neighbors. In this work, we elevate this question to utmost importance as the Topology Problem. We propose an attention mechanism that allows a graph to be constructed in a learned space that handles geometrically the flow of relevance, providing one solution to the Topology Problem. We test this architecture, called GravNetNorm, on the task of top jet tagging, and show that it is competitive in tagging accuracy, and uses far fewer computational resources than all other comparable models.

Equivariant Graph Neural Networks for Charged Particle Tracking

Graph neural networks (GNNs) have gained traction in high-energy physics (HEP) for their potential to improve accuracy and scalability. However, their resource-intensive nature and complex operations have motivated the development of symmetry-equivariant architectures. In this work, we introduce EuclidNet, a novel symmetry-equivariant GNN for charged particle tracking. EuclidNet leverages the graph representation of collision events and enforces rotational symmetry with respect to the detector's beamline axis, leading to a more efficient model. We benchmark EuclidNet against the state-of-the-art Interaction Network on the TrackML dataset, which simulates high-pileup conditions expected at the High-Luminosity Large Hadron Collider (HL-LHC). Our results show that EuclidNet achieves near-state-of-the-art performance at small model scales (<1000 parameters), outperforming the non-equivariant benchmarks. This study paves the way for future investigations into more resource-efficient GNN models for particle tracking in HEP experiments.

Graph Neural Networks in Particle Physics: Implementations, Innovations, and Challenges

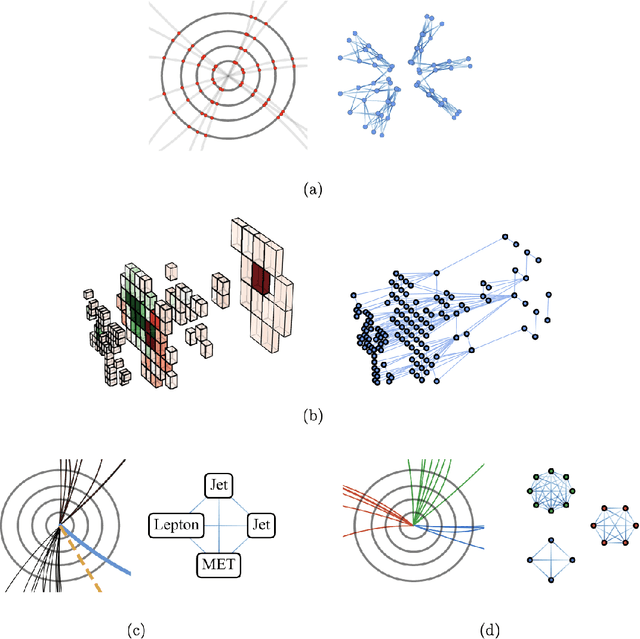
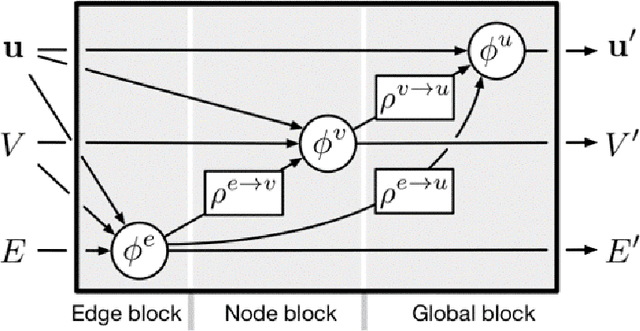
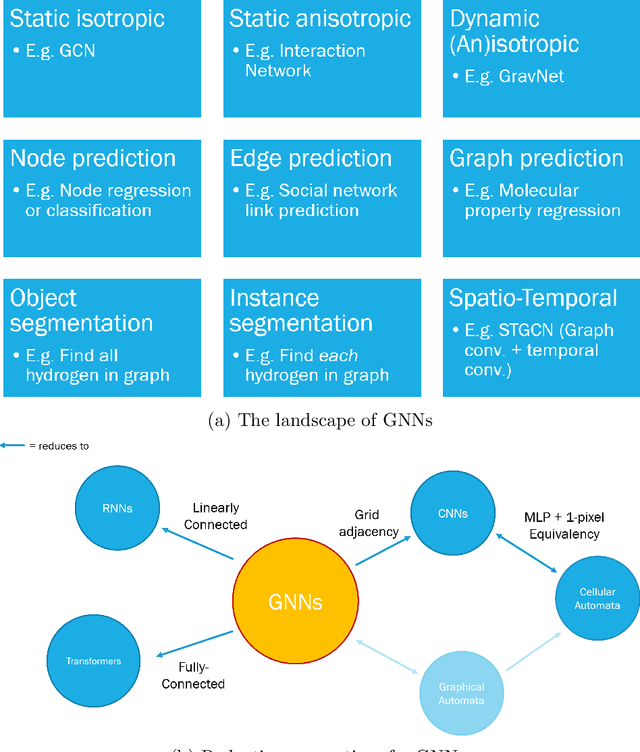
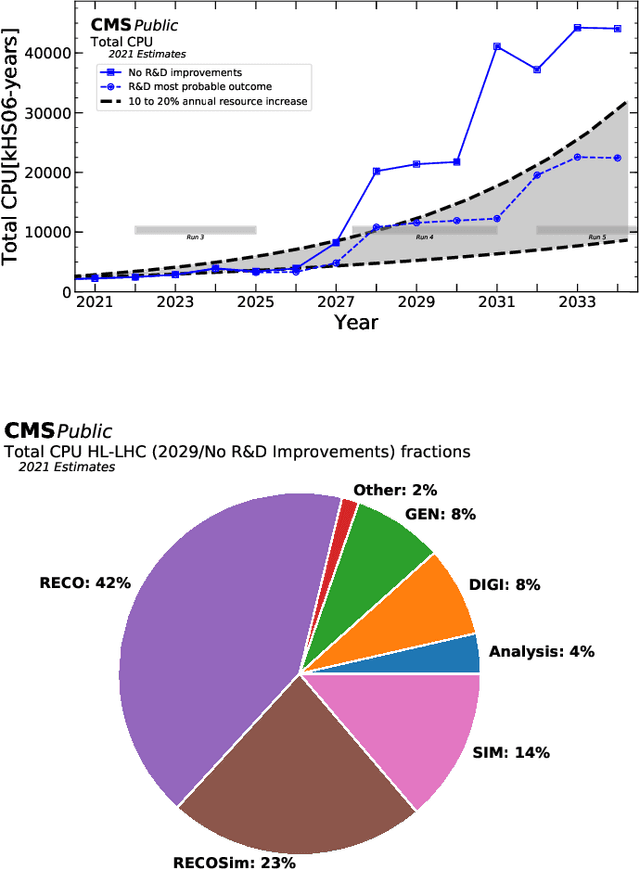
Many physical systems can be best understood as sets of discrete data with associated relationships. Where previously these sets of data have been formulated as series or image data to match the available machine learning architectures, with the advent of graph neural networks (GNNs), these systems can be learned natively as graphs. This allows a wide variety of high- and low-level physical features to be attached to measurements and, by the same token, a wide variety of HEP tasks to be accomplished by the same GNN architectures. GNNs have found powerful use-cases in reconstruction, tagging, generation and end-to-end analysis. With the wide-spread adoption of GNNs in industry, the HEP community is well-placed to benefit from rapid improvements in GNN latency and memory usage. However, industry use-cases are not perfectly aligned with HEP and much work needs to be done to best match unique GNN capabilities to unique HEP obstacles. We present here a range of these capabilities, predictions of which are currently being well-adopted in HEP communities, and which are still immature. We hope to capture the landscape of graph techniques in machine learning as well as point out the most significant gaps that are inhibiting potentially large leaps in research.

Symmetry Group Equivariant Architectures for Physics

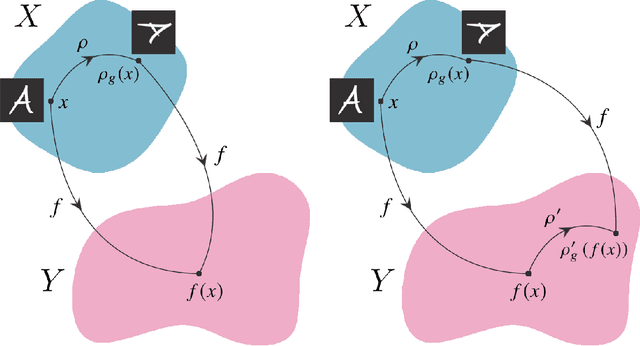
Physical theories grounded in mathematical symmetries are an essential component of our understanding of a wide range of properties of the universe. Similarly, in the domain of machine learning, an awareness of symmetries such as rotation or permutation invariance has driven impressive performance breakthroughs in computer vision, natural language processing, and other important applications. In this report, we argue that both the physics community and the broader machine learning community have much to understand and potentially to gain from a deeper investment in research concerning symmetry group equivariant machine learning architectures. For some applications, the introduction of symmetries into the fundamental structural design can yield models that are more economical (i.e. contain fewer, but more expressive, learned parameters), interpretable (i.e. more explainable or directly mappable to physical quantities), and/or trainable (i.e. more efficient in both data and computational requirements). We discuss various figures of merit for evaluating these models as well as some potential benefits and limitations of these methods for a variety of physics applications. Research and investment into these approaches will lay the foundation for future architectures that are potentially more robust under new computational paradigms and will provide a richer description of the physical systems to which they are applied.

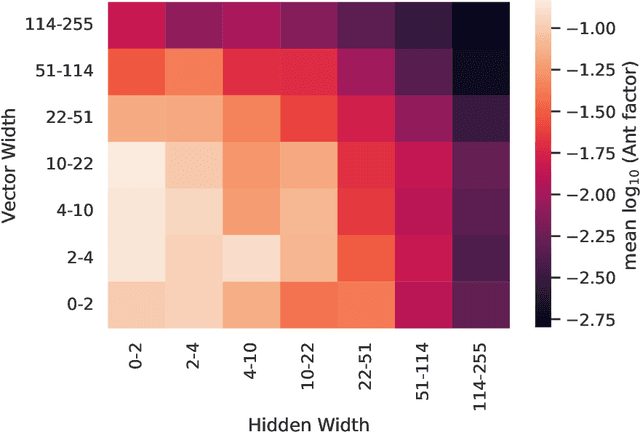
Semi-Equivariant GNN Architectures for Jet Tagging

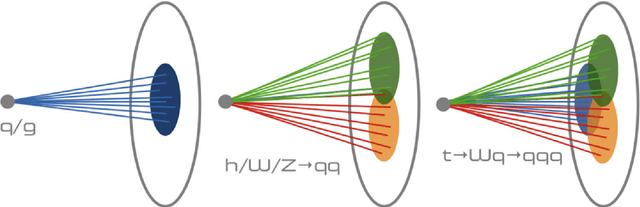
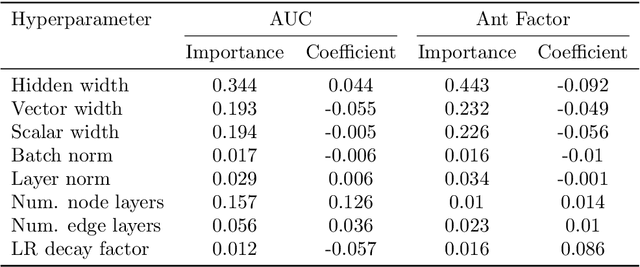
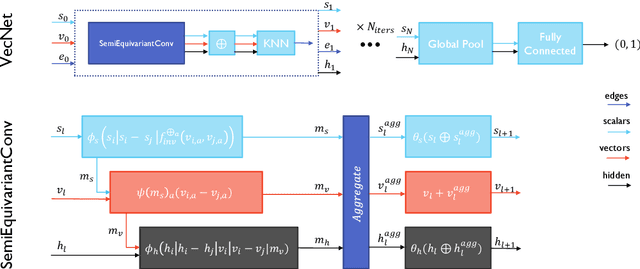
Composing Graph Neural Networks (GNNs) of operations that respect physical symmetries has been suggested to give better model performance with a smaller number of learnable parameters. However, real-world applications, such as in high energy physics have not born this out. We present the novel architecture VecNet that combines both symmetry-respecting and unconstrained operations to study and tune the degree of physics-informed GNNs. We introduce a novel metric, the \textit{ant factor}, to quantify the resource-efficiency of each configuration in the search-space. We find that a generalized architecture such as ours can deliver optimal performance in resource-constrained applications.

Physics and Computing Performance of the Exa.TrkX TrackML Pipeline

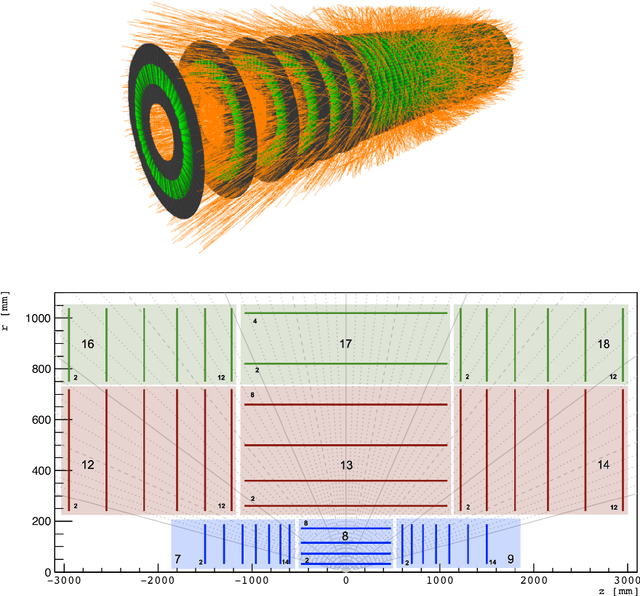
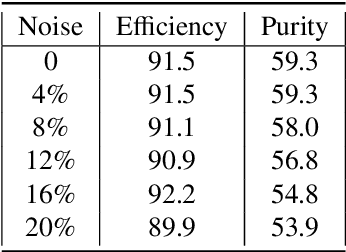
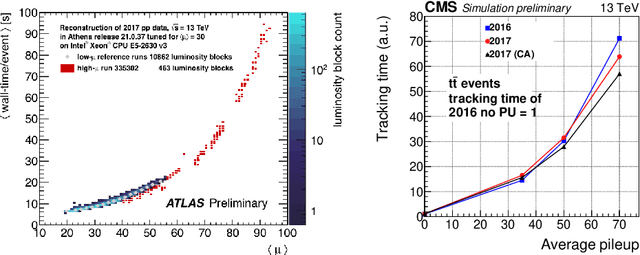
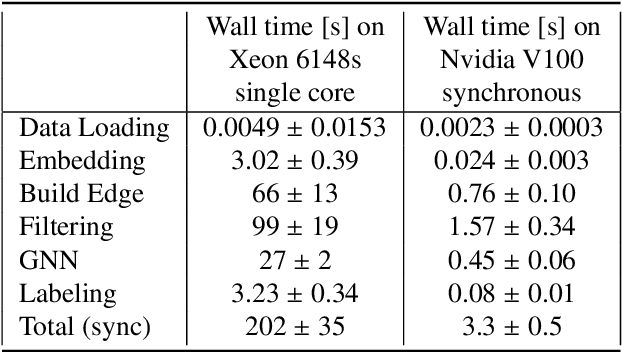
The Exa.TrkX project has applied geometric learning concepts such as metric learning and graph neural networks to HEP particle tracking. The Exa.TrkX tracking pipeline clusters detector measurements to form track candidates and filters them. The pipeline, originally developed using the TrackML dataset (a simulation of an LHC-like tracking detector), has been demonstrated on various detectors, including the DUNE LArTPC and the CMS High-Granularity Calorimeter. This paper documents new developments needed to study the physics and computing performance of the Exa.TrkX pipeline on the full TrackML dataset, a first step towards validating the pipeline using ATLAS and CMS data. The pipeline achieves tracking efficiency and purity similar to production tracking algorithms. Crucially for future HEP applications, the pipeline benefits significantly from GPU acceleration, and its computational requirements scale close to linearly with the number of particles in the event.

Track Seeding and Labelling with Embedded-space Graph Neural Networks

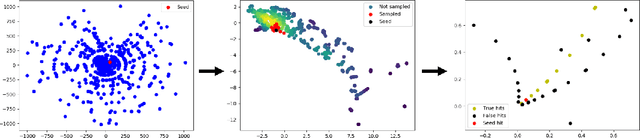
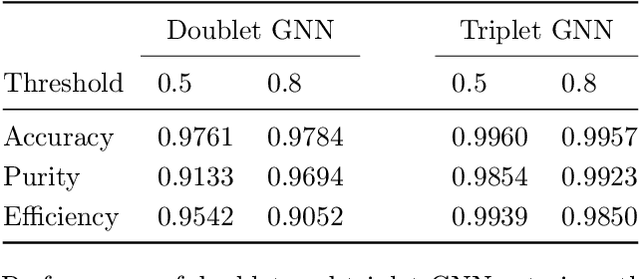
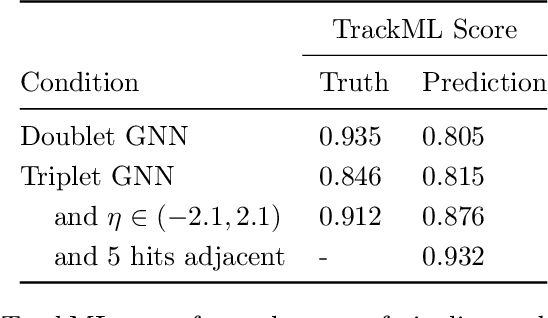
To address the unprecedented scale of HL-LHC data, the Exa.TrkX project is investigating a variety of machine learning approaches to particle track reconstruction. The most promising of these solutions, graph neural networks (GNN), process the event as a graph that connects track measurements (detector hits corresponding to nodes) with candidate line segments between the hits (corresponding to edges). Detector information can be associated with nodes and edges, enabling a GNN to propagate the embedded parameters around the graph and predict node-, edge- and graph-level observables. Previously, message-passing GNNs have shown success in predicting doublet likelihood, and we here report updates on the state-of-the-art architectures for this task. In addition, the Exa.TrkX project has investigated innovations in both graph construction, and embedded representations, in an effort to achieve fully learned end-to-end track finding. Hence, we present a suite of extensions to the original model, with encouraging results for hitgraph classification. In addition, we explore increased performance by constructing graphs from learned representations which contain non-linear metric structure, allowing for efficient clustering and neighborhood queries of data points. We demonstrate how this framework fits in with both traditional clustering pipelines, and GNN approaches. The embedded graphs feed into high-accuracy doublet and triplet classifiers, or can be used as an end-to-end track classifier by clustering in an embedded space. A set of post-processing methods improve performance with knowledge of the detector physics. Finally, we present numerical results on the TrackML particle tracking challenge dataset, where our framework shows favorable results in both seeding and track finding.