Jan T. Offermann
19 Parameters Is All You Need: Tiny Neural Networks for Particle Physics
Oct 24, 2023Abstract:As particle accelerators increase their collision rates, and deep learning solutions prove their viability, there is a growing need for lightweight and fast neural network architectures for low-latency tasks such as triggering. We examine the potential of one recent Lorentz- and permutation-symmetric architecture, PELICAN, and present its instances with as few as 19 trainable parameters that outperform generic architectures with tens of thousands of parameters when compared on the binary classification task of top quark jet tagging.
Explainable Equivariant Neural Networks for Particle Physics: PELICAN
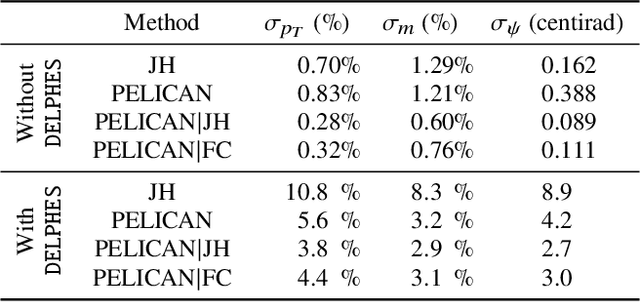
Jul 31, 2023Abstract:We present a comprehensive study of the PELICAN machine learning algorithm architecture in the context of both tagging (classification) and reconstructing (regression) Lorentz-boosted top quarks, including the difficult task of specifically identifying and measuring the $W$-boson inside the dense environment of the boosted hadronic final state. PELICAN is a novel permutation equivariant and Lorentz invariant or covariant aggregator network designed to overcome common limitations found in architectures applied to particle physics problems. Compared to many approaches that use non-specialized architectures that neglect underlying physics principles and require very large numbers of parameters, PELICAN employs a fundamentally symmetry group-based architecture that demonstrates benefits in terms of reduced complexity, increased interpretability, and raw performance. When tested on the standard task of Lorentz-boosted top quark tagging, PELICAN outperforms existing competitors with much lower model complexity and high sample efficiency. On the less common and more complex task of four-momentum regression, PELICAN also outperforms hand-crafted algorithms. We discuss the implications of symmetry-restricted architectures for the wider field of machine learning for physics.
PELICAN: Permutation Equivariant and Lorentz Invariant or Covariant Aggregator Network for Particle Physics
Nov 01, 2022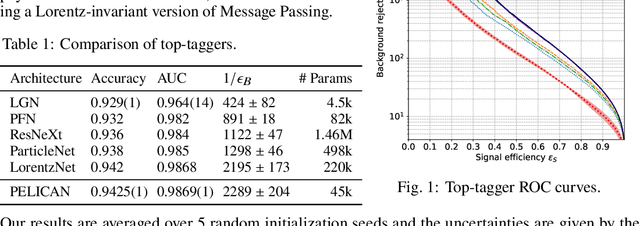
Abstract:Many current approaches to machine learning in particle physics use generic architectures that require large numbers of parameters and disregard underlying physics principles, limiting their applicability as scientific modeling tools. In this work, we present a machine learning architecture that uses a set of inputs maximally reduced with respect to the full 6-dimensional Lorentz symmetry, and is fully permutation-equivariant throughout. We study the application of this network architecture to the standard task of top quark tagging and show that the resulting network outperforms all existing competitors despite much lower model complexity. In addition, we present a Lorentz-covariant variant of the same network applied to a 4-momentum regression task.
Symmetry Group Equivariant Architectures for Physics
Mar 11, 2022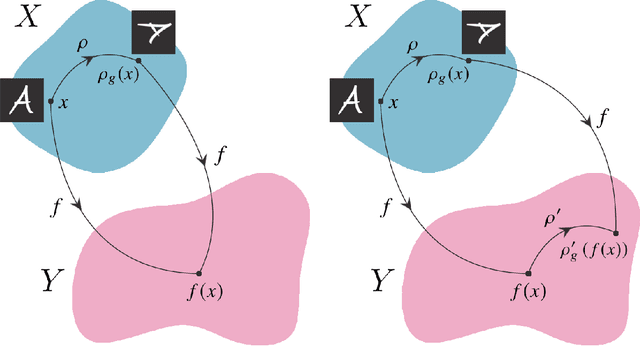
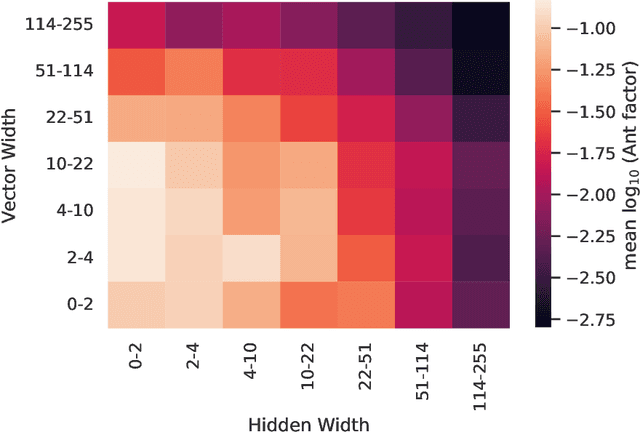
Abstract:Physical theories grounded in mathematical symmetries are an essential component of our understanding of a wide range of properties of the universe. Similarly, in the domain of machine learning, an awareness of symmetries such as rotation or permutation invariance has driven impressive performance breakthroughs in computer vision, natural language processing, and other important applications. In this report, we argue that both the physics community and the broader machine learning community have much to understand and potentially to gain from a deeper investment in research concerning symmetry group equivariant machine learning architectures. For some applications, the introduction of symmetries into the fundamental structural design can yield models that are more economical (i.e. contain fewer, but more expressive, learned parameters), interpretable (i.e. more explainable or directly mappable to physical quantities), and/or trainable (i.e. more efficient in both data and computational requirements). We discuss various figures of merit for evaluating these models as well as some potential benefits and limitations of these methods for a variety of physics applications. Research and investment into these approaches will lay the foundation for future architectures that are potentially more robust under new computational paradigms and will provide a richer description of the physical systems to which they are applied.
Lorentz Group Equivariant Neural Network for Particle Physics
Jun 08, 2020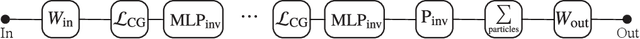
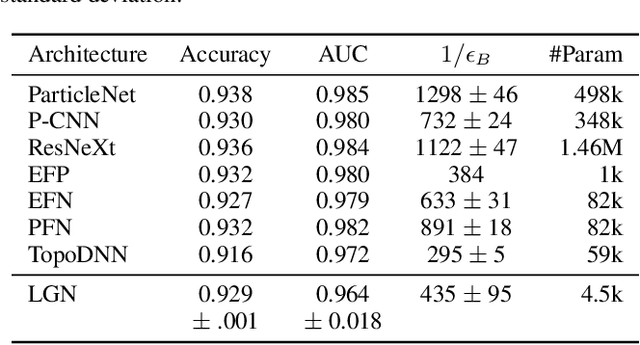
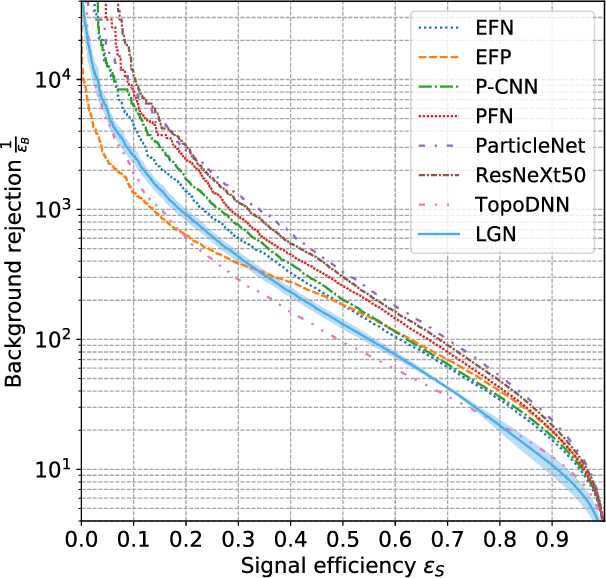
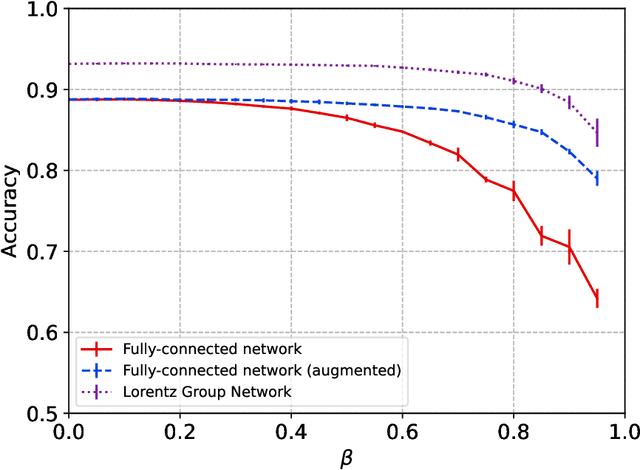
Abstract:We present a neural network architecture that is fully equivariant with respect to transformations under the Lorentz group, a fundamental symmetry of space and time in physics. The architecture is based on the theory of the finite-dimensional representations of the Lorentz group and the equivariant nonlinearity involves the tensor product. For classification tasks in particle physics, we demonstrate that such an equivariant architecture leads to drastically simpler models that have relatively few learnable parameters and are much more physically interpretable than leading approaches that use CNNs and point cloud approaches. The competitive performance of the network is demonstrated on a public classification dataset [27] for tagging top quark decays given energy-momenta of jet constituents produced in proton-proton collisions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge