Lorentz Group Equivariant Neural Network for Particle Physics
Paper and Code
Jun 08, 2020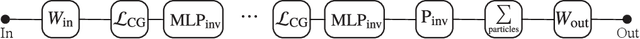
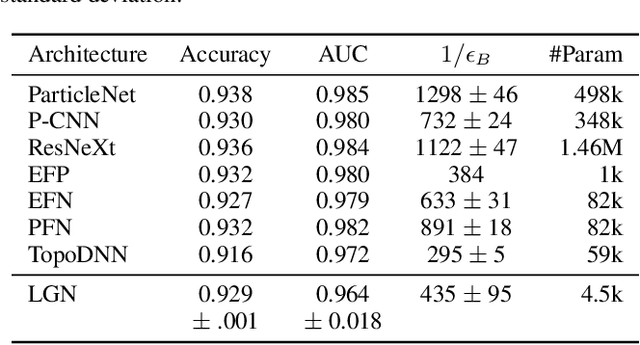
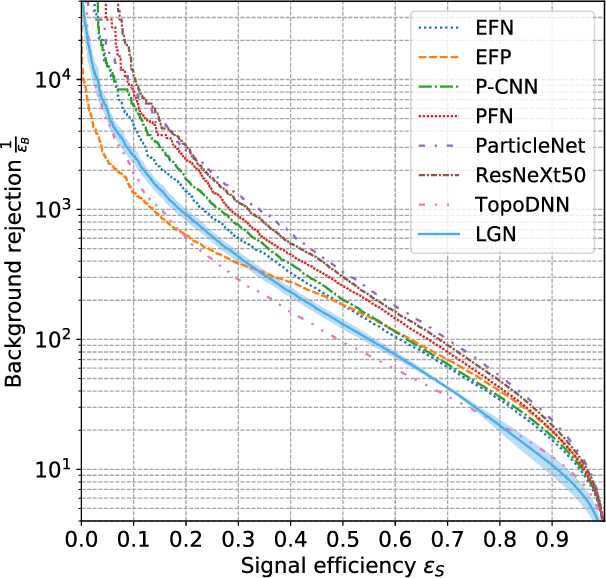
We present a neural network architecture that is fully equivariant with respect to transformations under the Lorentz group, a fundamental symmetry of space and time in physics. The architecture is based on the theory of the finite-dimensional representations of the Lorentz group and the equivariant nonlinearity involves the tensor product. For classification tasks in particle physics, we demonstrate that such an equivariant architecture leads to drastically simpler models that have relatively few learnable parameters and are much more physically interpretable than leading approaches that use CNNs and point cloud approaches. The competitive performance of the network is demonstrated on a public classification dataset [27] for tagging top quark decays given energy-momenta of jet constituents produced in proton-proton collisions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge