19 Parameters Is All You Need: Tiny Neural Networks for Particle Physics

As particle accelerators increase their collision rates, and deep learning solutions prove their viability, there is a growing need for lightweight and fast neural network architectures for low-latency tasks such as triggering. We examine the potential of one recent Lorentz- and permutation-symmetric architecture, PELICAN, and present its instances with as few as 19 trainable parameters that outperform generic architectures with tens of thousands of parameters when compared on the binary classification task of top quark jet tagging.

Explainable Equivariant Neural Networks for Particle Physics: PELICAN

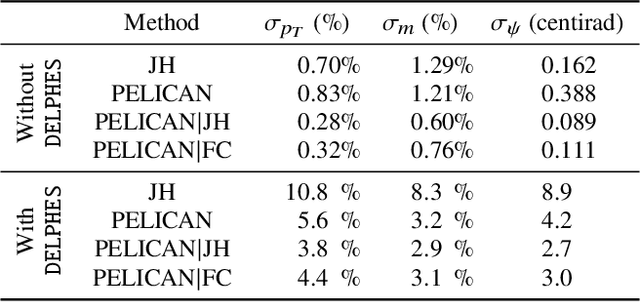
We present a comprehensive study of the PELICAN machine learning algorithm architecture in the context of both tagging (classification) and reconstructing (regression) Lorentz-boosted top quarks, including the difficult task of specifically identifying and measuring the $W$-boson inside the dense environment of the boosted hadronic final state. PELICAN is a novel permutation equivariant and Lorentz invariant or covariant aggregator network designed to overcome common limitations found in architectures applied to particle physics problems. Compared to many approaches that use non-specialized architectures that neglect underlying physics principles and require very large numbers of parameters, PELICAN employs a fundamentally symmetry group-based architecture that demonstrates benefits in terms of reduced complexity, increased interpretability, and raw performance. When tested on the standard task of Lorentz-boosted top quark tagging, PELICAN outperforms existing competitors with much lower model complexity and high sample efficiency. On the less common and more complex task of four-momentum regression, PELICAN also outperforms hand-crafted algorithms. We discuss the implications of symmetry-restricted architectures for the wider field of machine learning for physics.

PELICAN: Permutation Equivariant and Lorentz Invariant or Covariant Aggregator Network for Particle Physics

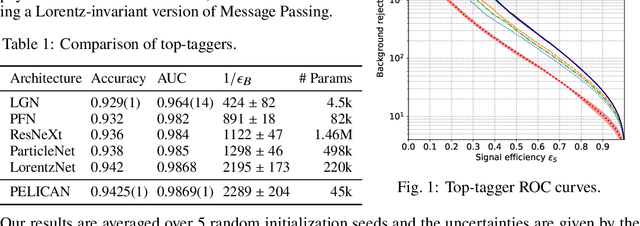
Many current approaches to machine learning in particle physics use generic architectures that require large numbers of parameters and disregard underlying physics principles, limiting their applicability as scientific modeling tools. In this work, we present a machine learning architecture that uses a set of inputs maximally reduced with respect to the full 6-dimensional Lorentz symmetry, and is fully permutation-equivariant throughout. We study the application of this network architecture to the standard task of top quark tagging and show that the resulting network outperforms all existing competitors despite much lower model complexity. In addition, we present a Lorentz-covariant variant of the same network applied to a 4-momentum regression task.