PELICAN: Permutation Equivariant and Lorentz Invariant or Covariant Aggregator Network for Particle Physics
Paper and Code
Nov 01, 2022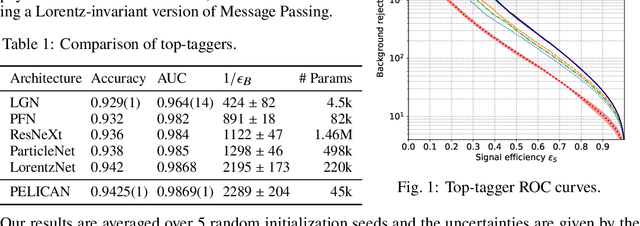
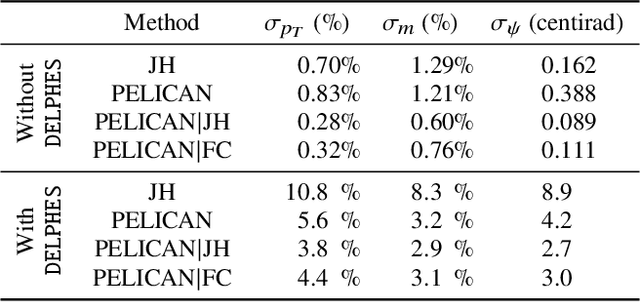
Many current approaches to machine learning in particle physics use generic architectures that require large numbers of parameters and disregard underlying physics principles, limiting their applicability as scientific modeling tools. In this work, we present a machine learning architecture that uses a set of inputs maximally reduced with respect to the full 6-dimensional Lorentz symmetry, and is fully permutation-equivariant throughout. We study the application of this network architecture to the standard task of top quark tagging and show that the resulting network outperforms all existing competitors despite much lower model complexity. In addition, we present a Lorentz-covariant variant of the same network applied to a 4-momentum regression task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge