Daiwei Zhang
Wheat3DGS: In-field 3D Reconstruction, Instance Segmentation and Phenotyping of Wheat Heads with Gaussian Splatting
Apr 09, 2025
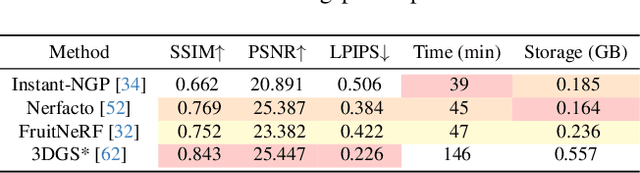
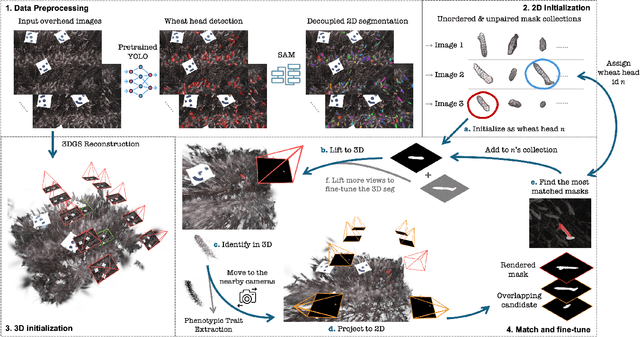

Abstract:Automated extraction of plant morphological traits is crucial for supporting crop breeding and agricultural management through high-throughput field phenotyping (HTFP). Solutions based on multi-view RGB images are attractive due to their scalability and affordability, enabling volumetric measurements that 2D approaches cannot directly capture. While advanced methods like Neural Radiance Fields (NeRFs) have shown promise, their application has been limited to counting or extracting traits from only a few plants or organs. Furthermore, accurately measuring complex structures like individual wheat heads-essential for studying crop yields-remains particularly challenging due to occlusions and the dense arrangement of crop canopies in field conditions. The recent development of 3D Gaussian Splatting (3DGS) offers a promising alternative for HTFP due to its high-quality reconstructions and explicit point-based representation. In this paper, we present Wheat3DGS, a novel approach that leverages 3DGS and the Segment Anything Model (SAM) for precise 3D instance segmentation and morphological measurement of hundreds of wheat heads automatically, representing the first application of 3DGS to HTFP. We validate the accuracy of wheat head extraction against high-resolution laser scan data, obtaining per-instance mean absolute percentage errors of 15.1%, 18.3%, and 40.2% for length, width, and volume. We provide additional comparisons to NeRF-based approaches and traditional Muti-View Stereo (MVS), demonstrating superior results. Our approach enables rapid, non-destructive measurements of key yield-related traits at scale, with significant implications for accelerating crop breeding and improving our understanding of wheat development.
MapSAM: Adapting Segment Anything Model for Automated Feature Detection in Historical Maps
Nov 11, 2024
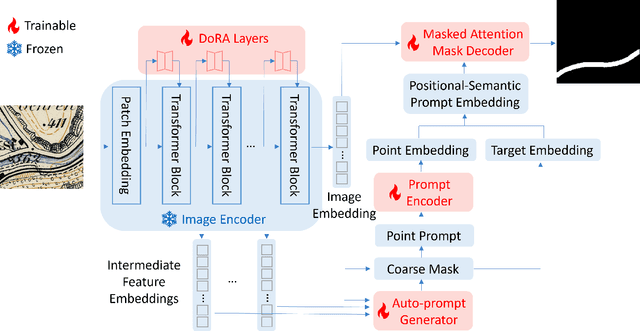
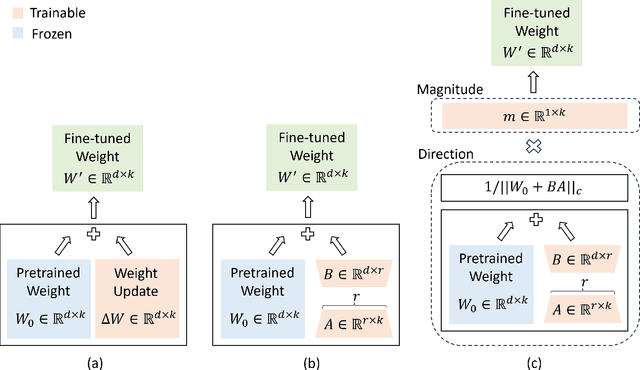

Abstract:Automated feature detection in historical maps can significantly accelerate the reconstruction of the geospatial past. However, this process is often constrained by the time-consuming task of manually digitizing sufficient high-quality training data. The emergence of visual foundation models, such as the Segment Anything Model (SAM), offers a promising solution due to their remarkable generalization capabilities and rapid adaptation to new data distributions. Despite this, directly applying SAM in a zero-shot manner to historical map segmentation poses significant challenges, including poor recognition of certain geospatial features and a reliance on input prompts, which limits its ability to be fully automated. To address these challenges, we introduce MapSAM, a parameter-efficient fine-tuning strategy that adapts SAM into a prompt-free and versatile solution for various downstream historical map segmentation tasks. Specifically, we employ Weight-Decomposed Low-Rank Adaptation (DoRA) to integrate domain-specific knowledge into the image encoder. Additionally, we develop an automatic prompt generation process, eliminating the need for manual input. We further enhance the positional prompt in SAM, transforming it into a higher-level positional-semantic prompt, and modify the cross-attention mechanism in the mask decoder with masked attention for more effective feature aggregation. The proposed MapSAM framework demonstrates promising performance across two distinct historical map segmentation tasks: one focused on linear features and the other on areal features. Experimental results show that it adapts well to various features, even when fine-tuned with extremely limited data (e.g. 10 shots).
EgoGaussian: Dynamic Scene Understanding from Egocentric Video with 3D Gaussian Splatting
Jun 28, 2024



Abstract:Human activities are inherently complex, and even simple household tasks involve numerous object interactions. To better understand these activities and behaviors, it is crucial to model their dynamic interactions with the environment. The recent availability of affordable head-mounted cameras and egocentric data offers a more accessible and efficient means to understand dynamic human-object interactions in 3D environments. However, most existing methods for human activity modeling either focus on reconstructing 3D models of hand-object or human-scene interactions or on mapping 3D scenes, neglecting dynamic interactions with objects. The few existing solutions often require inputs from multiple sources, including multi-camera setups, depth-sensing cameras, or kinesthetic sensors. To this end, we introduce EgoGaussian, the first method capable of simultaneously reconstructing 3D scenes and dynamically tracking 3D object motion from RGB egocentric input alone. We leverage the uniquely discrete nature of Gaussian Splatting and segment dynamic interactions from the background. Our approach employs a clip-level online learning pipeline that leverages the dynamic nature of human activities, allowing us to reconstruct the temporal evolution of the scene in chronological order and track rigid object motion. Additionally, our method automatically segments object and background Gaussians, providing 3D representations for both static scenes and dynamic objects. EgoGaussian outperforms previous NeRF and Dynamic Gaussian methods in challenging in-the-wild videos and we also qualitatively demonstrate the high quality of the reconstructed models.
Density Regression and Uncertainty Quantification with Bayesian Deep Noise Neural Networks
Jun 12, 2022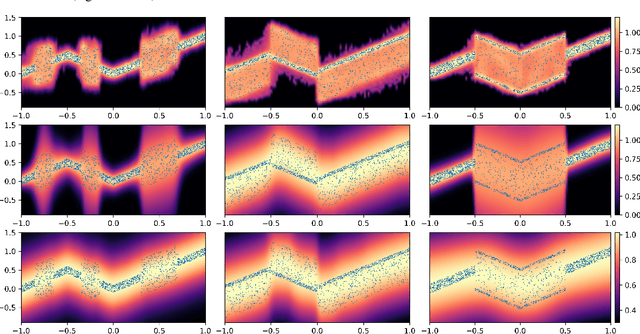
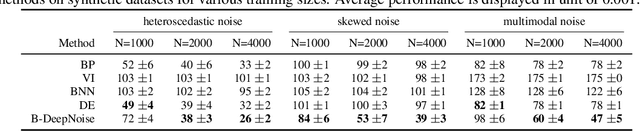
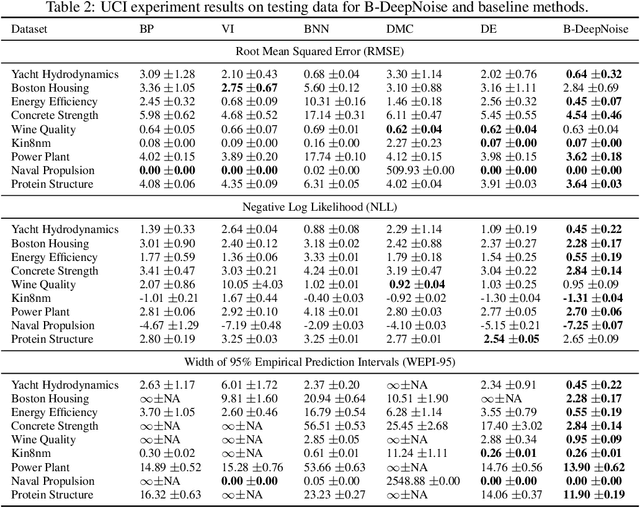
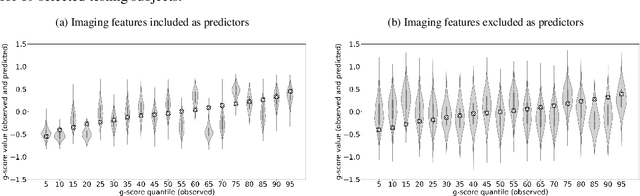
Abstract:Deep neural network (DNN) models have achieved state-of-the-art predictive accuracy in a wide range of supervised learning applications. However, accurately quantifying the uncertainty in DNN predictions remains a challenging task. For continuous outcome variables, an even more difficult problem is to estimate the predictive density function, which not only provides a natural quantification of the predictive uncertainty, but also fully captures the random variation in the outcome. In this work, we propose the Bayesian Deep Noise Neural Network (B-DeepNoise), which generalizes standard Bayesian DNNs by extending the random noise variable from the output layer to all hidden layers. The latent random noise equips B-DeepNoise with the flexibility to approximate highly complex predictive distributions and accurately quantify predictive uncertainty. For posterior computation, the unique structure of B-DeepNoise leads to a closed-form Gibbs sampling algorithm that iteratively simulates from the posterior full conditional distributions of the model parameters, circumventing computationally intensive Metropolis-Hastings methods. A theoretical analysis of B-DeepNoise establishes a recursive representation of the predictive distribution and decomposes the predictive variance with respect to the latent parameters. We evaluate B-DeepNoise against existing methods on benchmark regression datasets, demonstrating its superior performance in terms of prediction accuracy, uncertainty quantification accuracy, and uncertainty quantification efficiency. To illustrate our method's usefulness in scientific studies, we apply B-DeepNoise to predict general intelligence from neuroimaging features in the Adolescent Brain Cognitive Development (ABCD) project.
Image-on-Scalar Regression via Deep Neural Networks
Jun 17, 2020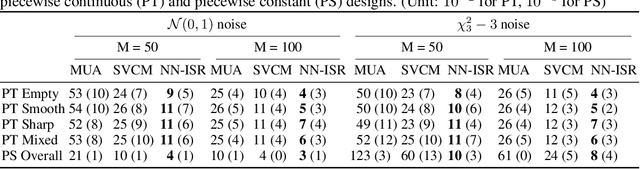
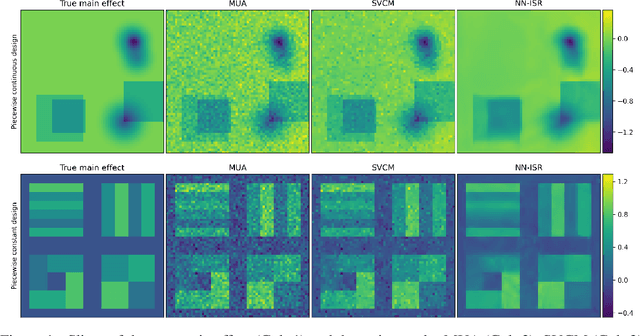
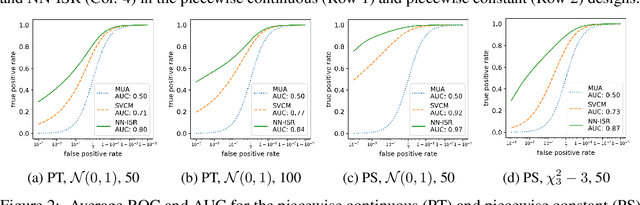
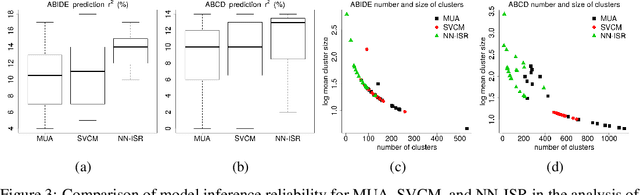
Abstract:A research topic of central interest in neuroimaging analysis is to study the associations between the massive imaging data and a set of covariates. This problem is challenging, due to the ultrahigh dimensionality, the high and heterogeneous level of noise, and the limited sample size of the imaging data. To address those challenges, we develop a novel image-on-scalar regression model, where the spatially-varying coefficients and the individual spatial effects are all constructed through deep neural networks (DNN). Compared with the existing solutions, our method is much more flexible in capturing the complex patterns among the brain signals, of which the noise level and the spatial smoothness appear to be heterogeneous across different brain regions. We develop a hybrid stochastic gradient descent estimation algorithm, and derive the asymptotic properties when the number of voxels grows much faster than the sample size. We show that the new method outperforms the existing ones through both extensive simulations and two neuroimaging data examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge