Density Regression and Uncertainty Quantification with Bayesian Deep Noise Neural Networks
Paper and Code
Jun 12, 2022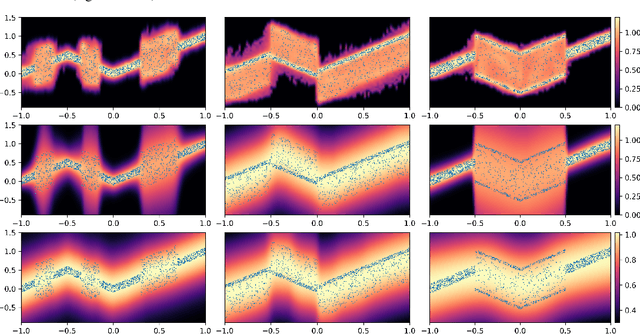
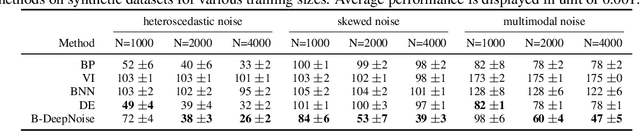
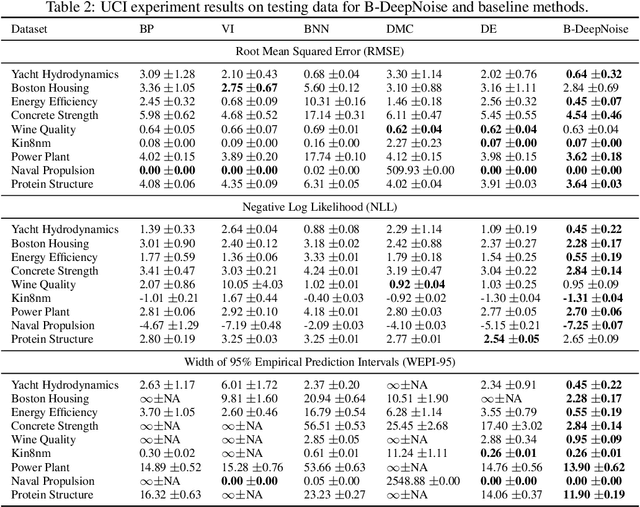
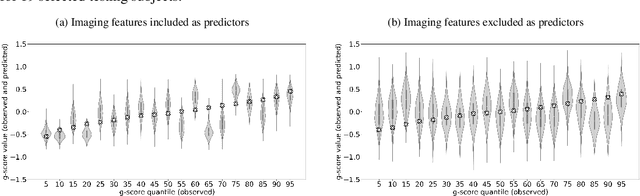
Deep neural network (DNN) models have achieved state-of-the-art predictive accuracy in a wide range of supervised learning applications. However, accurately quantifying the uncertainty in DNN predictions remains a challenging task. For continuous outcome variables, an even more difficult problem is to estimate the predictive density function, which not only provides a natural quantification of the predictive uncertainty, but also fully captures the random variation in the outcome. In this work, we propose the Bayesian Deep Noise Neural Network (B-DeepNoise), which generalizes standard Bayesian DNNs by extending the random noise variable from the output layer to all hidden layers. The latent random noise equips B-DeepNoise with the flexibility to approximate highly complex predictive distributions and accurately quantify predictive uncertainty. For posterior computation, the unique structure of B-DeepNoise leads to a closed-form Gibbs sampling algorithm that iteratively simulates from the posterior full conditional distributions of the model parameters, circumventing computationally intensive Metropolis-Hastings methods. A theoretical analysis of B-DeepNoise establishes a recursive representation of the predictive distribution and decomposes the predictive variance with respect to the latent parameters. We evaluate B-DeepNoise against existing methods on benchmark regression datasets, demonstrating its superior performance in terms of prediction accuracy, uncertainty quantification accuracy, and uncertainty quantification efficiency. To illustrate our method's usefulness in scientific studies, we apply B-DeepNoise to predict general intelligence from neuroimaging features in the Adolescent Brain Cognitive Development (ABCD) project.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge