Conflict and Congruency Effects in Large Language Models: In-Weight and In-Context Competition in a Verbal Conflict Task

Congruency effects, observed in conflict tasks such as Stroop and flanker tasks, have been investigated for nearly a century in psychology and neuroscience, but their mechanistic basis is not fully understood. We introduce a verbal-only LLM conflict task in which a prompt stem elicits a default same-color completion and an explicit rule either agrees with (congruent condition) or conflicts with (incongruent condition) the completion. Gemma-2-2B and six Pythia models ranging from 410M to 12B parameters showed strong default same-color tendencies, and six of seven models showed strong congruency effects. Using causal attribution analysis, attention analysis, and attention ablations, we identified distinct processing pathways in these LLMs: a pathway involving short-range attention to a superficial color cue that is preferentially activated in the congruent condition, and a pathway involving long-range attention to the rule prefix that is preferentially activated in the incongruent condition. Fine-tuning that strengthened the default same-color tendency had divergent effects on task conditions, reducing incongruent performance while increasing congruent performance. In contrast, increasing rule set size selectively impaired incongruent performance. These converging findings support an account in which congruency effects in this task arise from competition between an in-weight default mapping and an in-context rule-based mapping. More broadly, our findings illustrate how LLMs can serve as model systems for mechanistic analysis of competition between default and rule-governed response tendencies within a single learned network.

Cognitive Convergence: Deep Similarities Between Large Language Models and Human Cognition

LLMs are widely regarded as alien intelligences, systems whose cognitive operations are fundamentally unlike our own. Apparent similarities to human cognition are therefore often seen as the result of anthropomorphic projection. We argue that this framing is mistaken. LLMs clearly differ from humans in important respects, including their physical substrate, learning history, and the environments with which they interact. These differences make it all the more striking that contemporary LLM-based systems converge with human cognition on a number of principles of cognitive organization with longstanding support in cognitive science. We identify structural correspondences across five dimensions: inferential organization, computational architecture, representational structure, prediction-driven learning, and reinforcement-learning-like mechanisms supporting goal-directed action. These correspondences support a broader model of intelligent cognition in which core principles long used to explain human intelligence also characterize contemporary LLM-based systems.

An AI-Powered Research Assistant in the Lab: A Practical Guide for Text Analysis Through Iterative Collaboration with LLMs

Analyzing texts such as open-ended responses, headlines, or social media posts is a time- and labor-intensive process highly susceptible to bias. LLMs are promising tools for text analysis, using either a predefined (top-down) or a data-driven (bottom-up) taxonomy, without sacrificing quality. Here we present a step-by-step tutorial to efficiently develop, test, and apply taxonomies for analyzing unstructured data through an iterative and collaborative process between researchers and LLMs. Using personal goals provided by participants as an example, we demonstrate how to write prompts to review datasets and generate a taxonomy of life domains, evaluate and refine the taxonomy through prompt and direct modifications, test the taxonomy and assess intercoder agreements, and apply the taxonomy to categorize an entire dataset with high intercoder reliability. We discuss the possibilities and limitations of using LLMs for text analysis.

Image-on-Scalar Regression via Deep Neural Networks

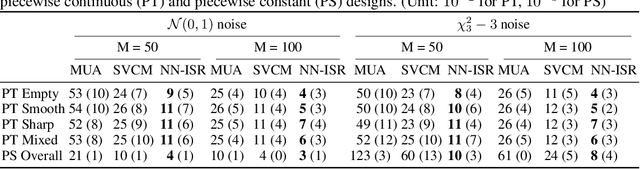
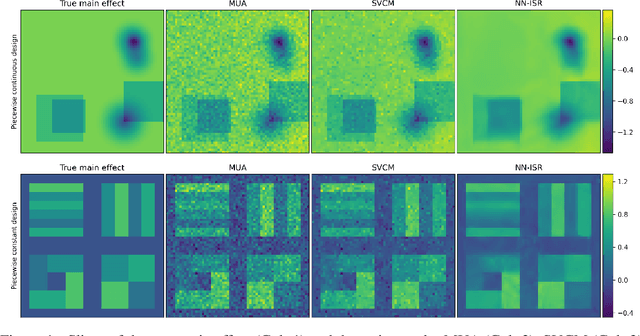
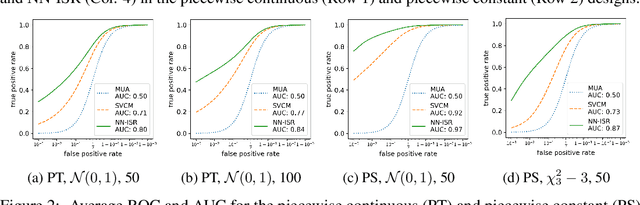
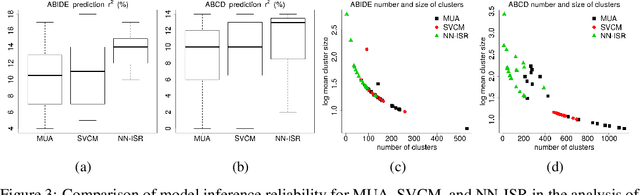
A research topic of central interest in neuroimaging analysis is to study the associations between the massive imaging data and a set of covariates. This problem is challenging, due to the ultrahigh dimensionality, the high and heterogeneous level of noise, and the limited sample size of the imaging data. To address those challenges, we develop a novel image-on-scalar regression model, where the spatially-varying coefficients and the individual spatial effects are all constructed through deep neural networks (DNN). Compared with the existing solutions, our method is much more flexible in capturing the complex patterns among the brain signals, of which the noise level and the spatial smoothness appear to be heterogeneous across different brain regions. We develop a hybrid stochastic gradient descent estimation algorithm, and derive the asymptotic properties when the number of voxels grows much faster than the sample size. We show that the new method outperforms the existing ones through both extensive simulations and two neuroimaging data examples.

A Domain Guided CNN Architecture for Predicting Age from Structural Brain Images

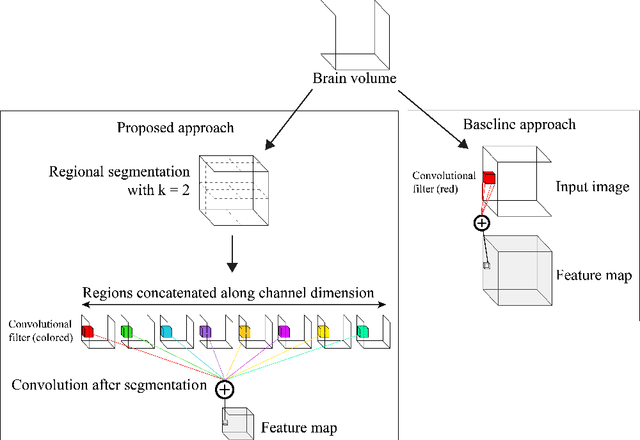
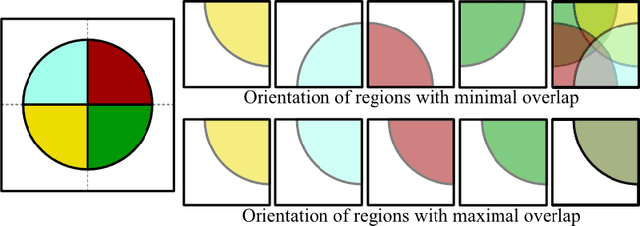
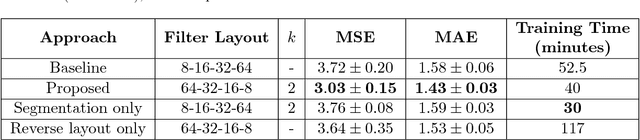
Given the wide success of convolutional neural networks (CNNs) applied to natural images, researchers have begun to apply them to neuroimaging data. To date, however, exploration of novel CNN architectures tailored to neuroimaging data has been limited. Several recent works fail to leverage the 3D structure of the brain, instead treating the brain as a set of independent 2D slices. Approaches that do utilize 3D convolutions rely on architectures developed for object recognition tasks in natural 2D images. Such architectures make assumptions about the input that may not hold for neuroimaging. For example, existing architectures assume that patterns in the brain exhibit translation invariance. However, a pattern in the brain may have different meaning depending on where in the brain it is located. There is a need to explore novel architectures that are tailored to brain images. We present two simple modifications to existing CNN architectures based on brain image structure. Applied to the task of brain age prediction, our network achieves a mean absolute error (MAE) of 1.4 years and trains 30% faster than a CNN baseline that achieves a MAE of 1.6 years. Our results suggest that lessons learned from developing models on natural images may not directly transfer to neuroimaging tasks. Instead, there remains a large space of unexplored questions regarding model development in this area, whose answers may differ from conventional wisdom.

Disease Prediction based on Functional Connectomes using a Scalable and Spatially-Informed Support Vector Machine

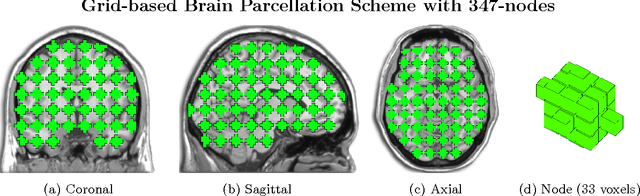
Substantial evidence indicates that major psychiatric disorders are associated with distributed neural dysconnectivity, leading to strong interest in using neuroimaging methods to accurately predict disorder status. In this work, we are specifically interested in a multivariate approach that uses features derived from whole-brain resting state functional connectomes. However, functional connectomes reside in a high dimensional space, which complicates model interpretation and introduces numerous statistical and computational challenges. Traditional feature selection techniques are used to reduce data dimensionality, but are blind to the spatial structure of the connectomes. We propose a regularization framework where the 6-D structure of the functional connectome is explicitly taken into account via the fused Lasso or the GraphNet regularizer. Our method only restricts the loss function to be convex and margin-based, allowing non-differentiable loss functions such as the hinge-loss to be used. Using the fused Lasso or GraphNet regularizer with the hinge-loss leads to a structured sparse support vector machine (SVM) with embedded feature selection. We introduce a novel efficient optimization algorithm based on the augmented Lagrangian and the classical alternating direction method, which can solve both fused Lasso and GraphNet regularized SVM with very little modification. We also demonstrate that the inner subproblems of the algorithm can be solved efficiently in analytic form by coupling the variable splitting strategy with a data augmentation scheme. Experiments on simulated data and resting state scans from a large schizophrenia dataset show that our proposed approach can identify predictive regions that are spatially contiguous in the 6-D "connectome space," offering an additional layer of interpretability that could provide new insights about various disease processes.