Leveraging Large Language Models for Learning Complex Legal Concepts through Storytelling

Making legal knowledge accessible to non-experts is crucial for enhancing general legal literacy and encouraging civic participation in democracy. However, legal documents are often challenging to understand for people without legal backgrounds. In this paper, we present a novel application of large language models (LLMs) in legal education to help non-experts learn intricate legal concepts through storytelling, an effective pedagogical tool in conveying complex and abstract concepts. We also introduce a new dataset LegalStories, which consists of 295 complex legal doctrines, each accompanied by a story and a set of multiple-choice questions generated by LLMs. To construct the dataset, we experiment with various LLMs to generate legal stories explaining these concepts. Furthermore, we use an expert-in-the-loop method to iteratively design multiple-choice questions. Then, we evaluate the effectiveness of storytelling with LLMs through an RCT experiment with legal novices on 10 samples from the dataset. We find that LLM-generated stories enhance comprehension of legal concepts and interest in law among non-native speakers compared to only definitions. Moreover, stories consistently help participants relate legal concepts to their lives. Finally, we find that learning with stories shows a higher retention rate for non-native speakers in the follow-up assessment. Our work has strong implications for using LLMs in promoting teaching and learning in the legal field and beyond.

Inference post Selection of Group-sparse Regression Models

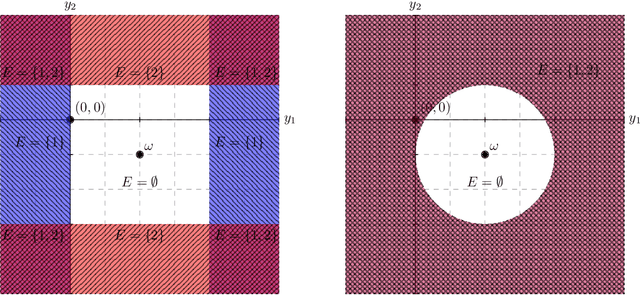
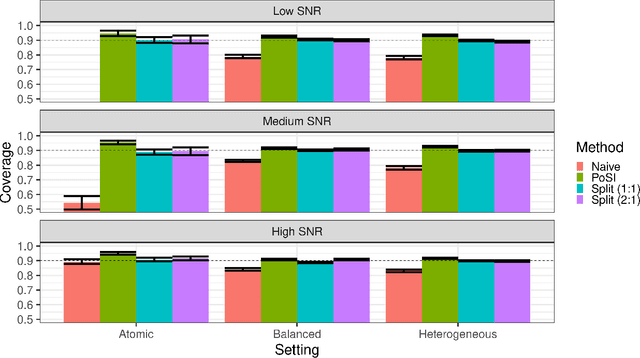
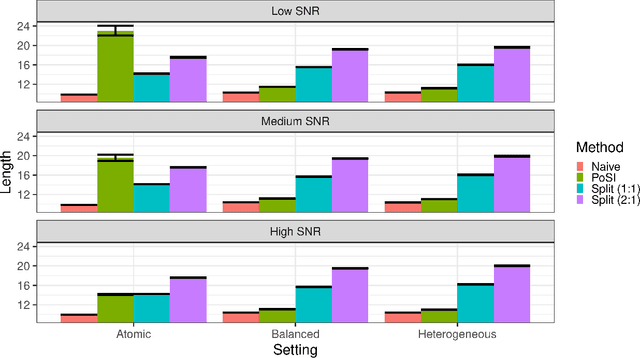
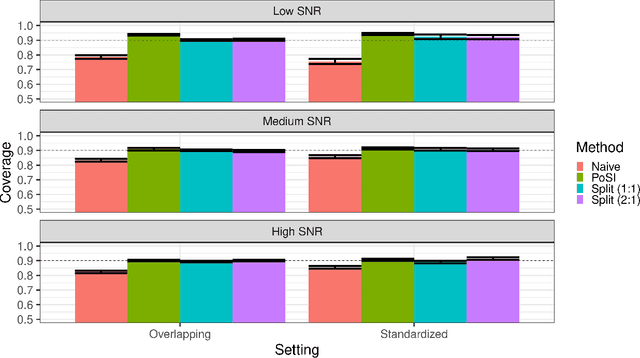
Conditional inference provides a rigorous approach to counter bias when data from automated model selections is reused for inference. We develop in this paper a statistically consistent Bayesian framework to assess uncertainties within linear models that are informed by grouped sparsities in covariates. Finding wide applications when genes, proteins, genetic variants, neuroimaging measurements are grouped respectively by their biological pathways, molecular functions, regulatory regions, cognitive roles, these models are selected through a useful class of group-sparse learning algorithms. An adjustment factor to account precisely for the selection of promising groups, deployed with a generalized version of Laplace-type approximations is the centerpiece of our new methods. Accommodating well known group-sparse models such as those selected by the Group LASSO, the overlapping Group LASSO, the sparse Group LASSO etc., we illustrate the efficacy of our methodology in extensive experiments and on data from a human neuroimaging application.

Network classification with applications to brain connectomics

While statistical analysis of a single network has received a lot of attention in recent years, with a focus on social networks, analysis of a sample of networks presents its own challenges which require a different set of analytic tools. Here we study the problem of classification of networks with labeled nodes, motivated by applications in neuroimaging. Brain networks are constructed from imaging data to represent functional connectivity between regions of the brain, and previous work has shown the potential of such networks to distinguish between various brain disorders, giving rise to a network classification problem. Existing approaches tend to either treat all edge weights as a long vector, ignoring the network structure, or focus on graph topology as represented by summary measures while ignoring the edge weights. Our goal is to design a classification method that uses both the individual edge information and the network structure of the data in a computationally efficient way, and that can produce a parsimonious and interpretable representation of differences in brain connectivity patterns between classes. We propose a graph classification method that uses edge weights as predictors but incorporates the network nature of the data via penalties that promote sparsity in the number of nodes, in addition to the usual sparsity penalties that encourage selection of edges. We implement the method via efficient convex optimization and provide a detailed analysis of data from two fMRI studies of schizophrenia.

Disease Prediction based on Functional Connectomes using a Scalable and Spatially-Informed Support Vector Machine

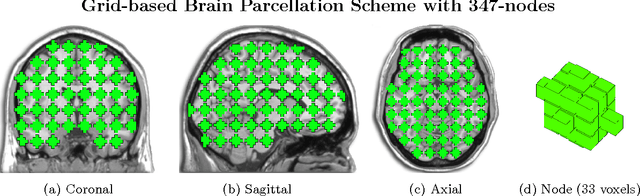
Substantial evidence indicates that major psychiatric disorders are associated with distributed neural dysconnectivity, leading to strong interest in using neuroimaging methods to accurately predict disorder status. In this work, we are specifically interested in a multivariate approach that uses features derived from whole-brain resting state functional connectomes. However, functional connectomes reside in a high dimensional space, which complicates model interpretation and introduces numerous statistical and computational challenges. Traditional feature selection techniques are used to reduce data dimensionality, but are blind to the spatial structure of the connectomes. We propose a regularization framework where the 6-D structure of the functional connectome is explicitly taken into account via the fused Lasso or the GraphNet regularizer. Our method only restricts the loss function to be convex and margin-based, allowing non-differentiable loss functions such as the hinge-loss to be used. Using the fused Lasso or GraphNet regularizer with the hinge-loss leads to a structured sparse support vector machine (SVM) with embedded feature selection. We introduce a novel efficient optimization algorithm based on the augmented Lagrangian and the classical alternating direction method, which can solve both fused Lasso and GraphNet regularized SVM with very little modification. We also demonstrate that the inner subproblems of the algorithm can be solved efficiently in analytic form by coupling the variable splitting strategy with a data augmentation scheme. Experiments on simulated data and resting state scans from a large schizophrenia dataset show that our proposed approach can identify predictive regions that are spatially contiguous in the 6-D "connectome space," offering an additional layer of interpretability that could provide new insights about various disease processes.