Inference post Selection of Group-sparse Regression Models
Paper and Code
Dec 31, 2020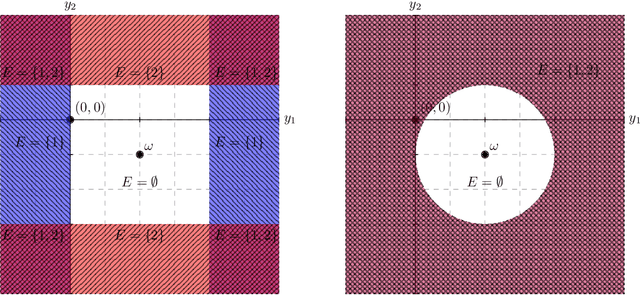
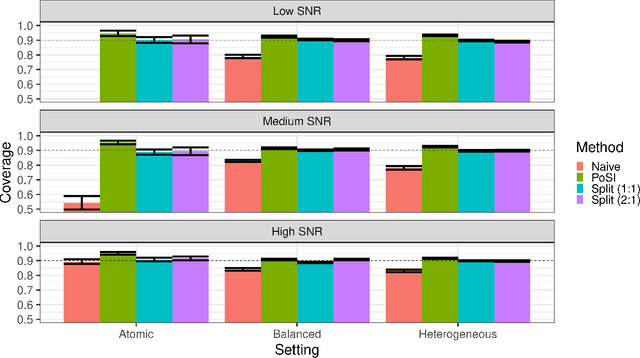
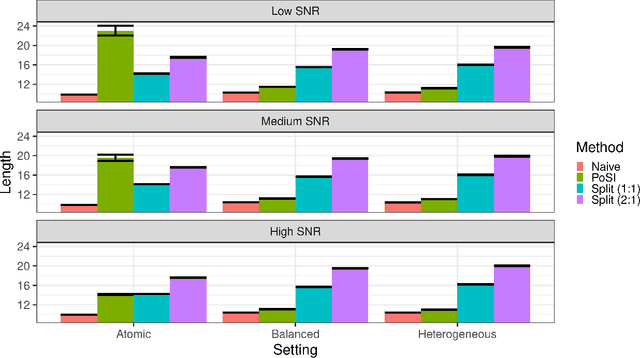
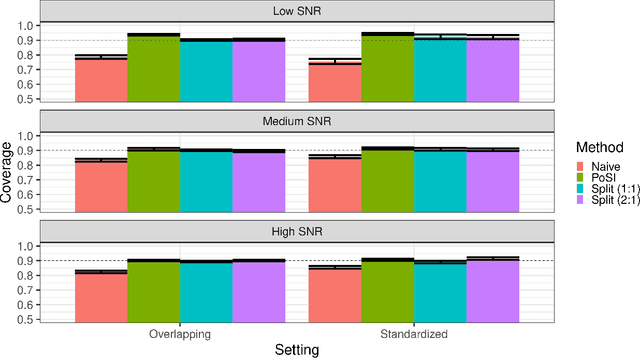
Conditional inference provides a rigorous approach to counter bias when data from automated model selections is reused for inference. We develop in this paper a statistically consistent Bayesian framework to assess uncertainties within linear models that are informed by grouped sparsities in covariates. Finding wide applications when genes, proteins, genetic variants, neuroimaging measurements are grouped respectively by their biological pathways, molecular functions, regulatory regions, cognitive roles, these models are selected through a useful class of group-sparse learning algorithms. An adjustment factor to account precisely for the selection of promising groups, deployed with a generalized version of Laplace-type approximations is the centerpiece of our new methods. Accommodating well known group-sparse models such as those selected by the Group LASSO, the overlapping Group LASSO, the sparse Group LASSO etc., we illustrate the efficacy of our methodology in extensive experiments and on data from a human neuroimaging application.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge