Image-on-Scalar Regression via Deep Neural Networks

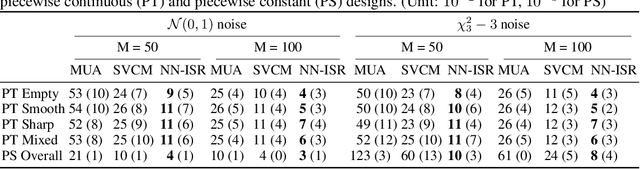
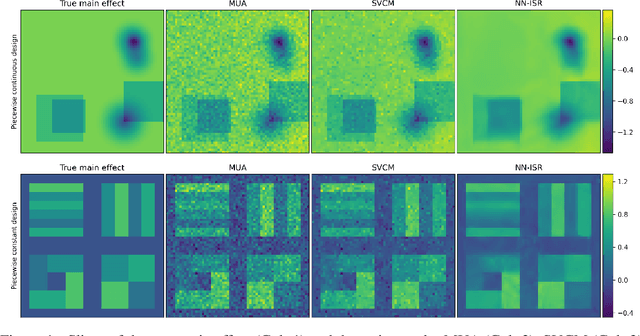
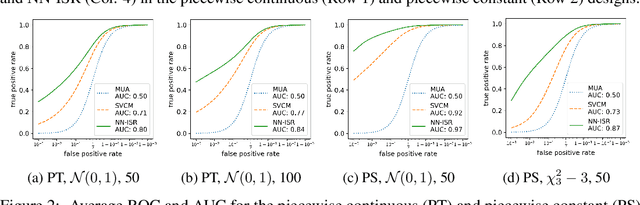
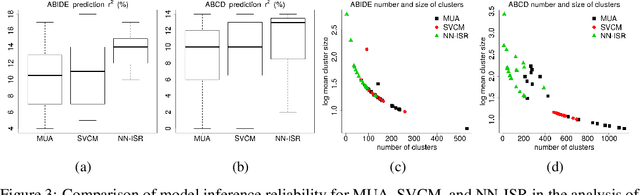
A research topic of central interest in neuroimaging analysis is to study the associations between the massive imaging data and a set of covariates. This problem is challenging, due to the ultrahigh dimensionality, the high and heterogeneous level of noise, and the limited sample size of the imaging data. To address those challenges, we develop a novel image-on-scalar regression model, where the spatially-varying coefficients and the individual spatial effects are all constructed through deep neural networks (DNN). Compared with the existing solutions, our method is much more flexible in capturing the complex patterns among the brain signals, of which the noise level and the spatial smoothness appear to be heterogeneous across different brain regions. We develop a hybrid stochastic gradient descent estimation algorithm, and derive the asymptotic properties when the number of voxels grows much faster than the sample size. We show that the new method outperforms the existing ones through both extensive simulations and two neuroimaging data examples.