Heterogeneous Team Coordination on Partially Observable Graphs with Realistic Communication

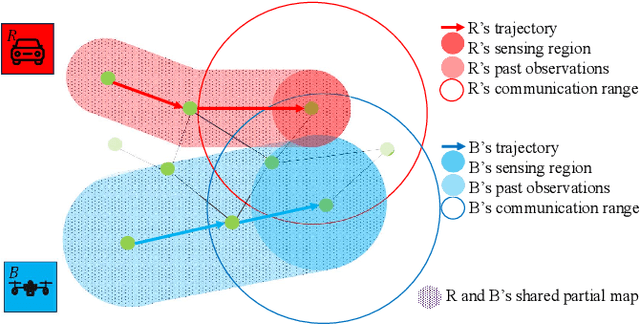
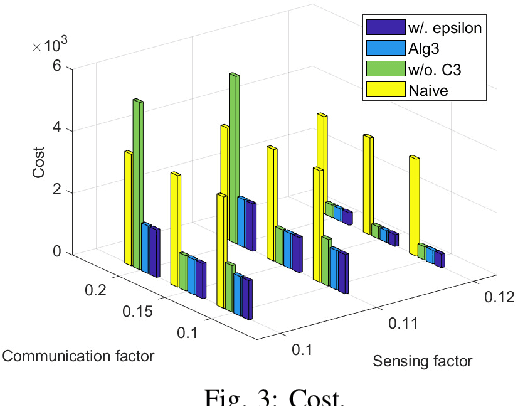
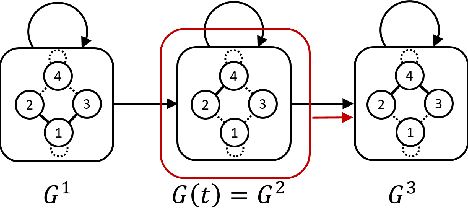
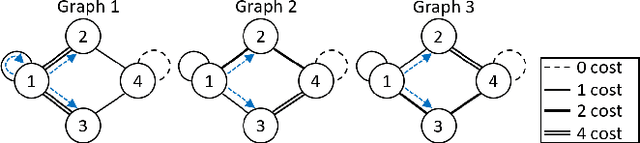
Team Coordination on Graphs with Risky Edges (\textsc{tcgre}) is a recently proposed problem, in which robots find paths to their goals while considering possible coordination to reduce overall team cost. However, \textsc{tcgre} assumes that the \emph{entire} environment is available to a \emph{homogeneous} robot team with \emph{ubiquitous} communication. In this paper, we study an extended version of \textsc{tcgre}, called \textsc{hpr-tcgre}, with three relaxations: Heterogeneous robots, Partial observability, and Realistic communication. To this end, we form a new combinatorial optimization problem on top of \textsc{tcgre}. After analysis, we divide it into two sub-problems, one for robots moving individually, another for robots in groups, depending on their communication availability. Then, we develop an algorithm that exploits real-time partial maps to solve local shortest path(s) problems, with a A*-like sub-goal(s) assignment mechanism that explores potential coordination opportunities for global interests. Extensive experiments indicate that our algorithm is able to produce team coordination behaviors in order to reduce overall cost even with our three relaxations.

Multi-Robot Coordination Induced in Hazardous Environments through an Adversarial Graph-Traversal Game

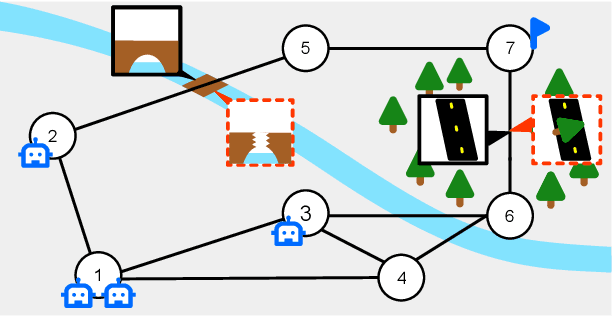
This paper presents a game theoretic formulation of a graph traversal problem, with applications to robots moving through hazardous environments in the presence of an adversary, as in military and security applications. The blue team of robots moves in an environment modeled by a time-varying graph, attempting to reach some goal with minimum cost, while the red team controls how the graph changes to maximize the cost. The problem is formulated as a stochastic game, so that Nash equilibrium strategies can be computed numerically. Bounds are provided for the game value, with a guarantee that it solves the original problem. Numerical simulations demonstrate the results and the effectiveness of this method, particularly showing the benefit of mixing actions for both players, as well as beneficial coordinated behavior, where blue robots split up and/or synchronize to traverse risky edges.

Learning Coordinated Maneuver in Adversarial Environments

This paper aims to solve the coordination of a team of robots traversing a route in the presence of adversaries with random positions. Our goal is to minimize the overall cost of the team, which is determined by (i) the accumulated risk when robots stay in adversary-impacted zones and (ii) the mission completion time. During traversal, robots can reduce their speed and act as a `guard' (the slower, the better), which will decrease the risks certain adversary incurs. This leads to a trade-off between the robots' guarding behaviors and their travel speeds. The formulated problem is highly non-convex and cannot be efficiently solved by existing algorithms. Our approach includes a theoretical analysis of the robots' behaviors for the single-adversary case. As the scale of the problem expands, solving the optimal solution using optimization approaches is challenging, therefore, we employ reinforcement learning techniques by developing new encoding and policy-generating methods. Simulations demonstrate that our learning methods can efficiently produce team coordination behaviors. We discuss the reasoning behind these behaviors and explain why they reduce the overall team cost.

Bi-CL: A Reinforcement Learning Framework for Robots Coordination Through Bi-level Optimization

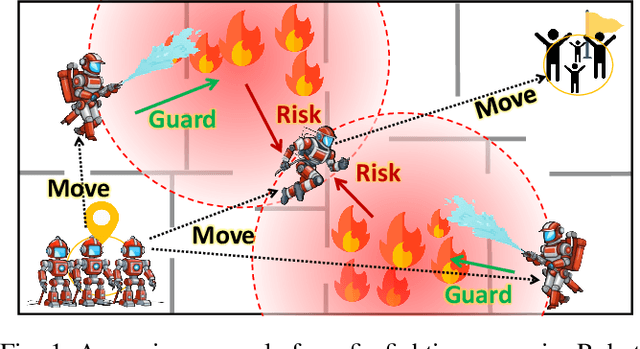
In multi-robot systems, achieving coordinated missions remains a significant challenge due to the coupled nature of coordination behaviors and the lack of global information for individual robots. To mitigate these challenges, this paper introduces a novel approach, Bi-level Coordination Learning (Bi-CL), that leverages a bi-level optimization structure within a centralized training and decentralized execution paradigm. Our bi-level reformulation decomposes the original problem into a reinforcement learning level with reduced action space, and an imitation learning level that gains demonstrations from a global optimizer. Both levels contribute to improved learning efficiency and scalability. We note that robots' incomplete information leads to mismatches between the two levels of learning models. To address this, Bi-CL further integrates an alignment penalty mechanism, aiming to minimize the discrepancy between the two levels without degrading their training efficiency. We introduce a running example to conceptualize the problem formulation and apply Bi-CL to two variations of this example: route-based and graph-based scenarios. Simulation results demonstrate that Bi-CL can learn more efficiently and achieve comparable performance with traditional multi-agent reinforcement learning baselines for multi-robot coordination.

Scaling Team Coordination on Graphs with Reinforcement Learning

This paper studies Reinforcement Learning (RL) techniques to enable team coordination behaviors in graph environments with support actions among teammates to reduce the costs of traversing certain risky edges in a centralized manner. While classical approaches can solve this non-standard multi-agent path planning problem by converting the original Environment Graph (EG) into a Joint State Graph (JSG) to implicitly incorporate the support actions, those methods do not scale well to large graphs and teams. To address this curse of dimensionality, we propose to use RL to enable agents to learn such graph traversal and teammate supporting behaviors in a data-driven manner. Specifically, through a new formulation of the team coordination on graphs with risky edges problem into Markov Decision Processes (MDPs) with a novel state and action space, we investigate how RL can solve it in two paradigms: First, we use RL for a team of agents to learn how to coordinate and reach the goal with minimal cost on a single EG. We show that RL efficiently solves problems with up to 20/4 or 25/3 nodes/agents, using a fraction of the time needed for JSG to solve such complex problems; Second, we learn a general RL policy for any $N$-node EGs to produce efficient supporting behaviors. We present extensive experiments and compare our RL approaches against their classical counterparts.

Manta Ray Inspired Flapping-Wing Blimp

Lighter-than-air vehicles or blimps, are an evolving platform in robotics with several beneficial properties such as energy efficiency, collision resistance, and ability to work in close proximity to human users. While existing blimp designs have mainly used propeller-based propulsion, we focus our attention to an alternate locomotion method, flapping wings. Specifically, this paper introduces a flapping-wing blimp inspired by manta rays, in contrast to existing research on flapping-wing vehicles that draw inspiration from insects or birds. We present the overall design and control scheme of the blimp as well as the analysis on how the wing performs. The effects of wing shape and flapping characteristics on the thrust generation are studied experimentally. We also demonstrate that the flapping-wing blimp has a significant range advantage over a propeller-based system.

Lighter-Than-Air Autonomous Ball Capture and Scoring Robot -- Design, Development, and Deployment

This paper describes the full end-to-end design of our primary scoring agent in an aerial autonomous robotics competition from April 2023. As open-ended robotics competitions become more popular, we wish to begin documenting successful team designs and approaches. The intended audience of this paper is not only any future or potential participant in this particular national Defend The Republic (DTR) competition, but rather anyone thinking about designing their first robot or system to be entered in a competition with clear goals. Future DTR participants can and should either build on the ideas here, or find new alternate strategies that can defeat the most successful design last time. For non-DTR participants but students interested in robotics competitions, identifying the minimum viable system needed to be competitive is still important in helping manage time and prioritizing tasks that are crucial to competition success first.

Target Defense against Sequentially Arriving Intruders

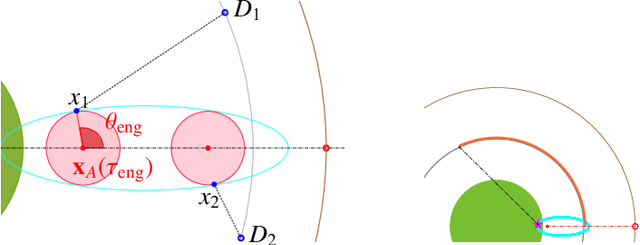
We consider a variant of the target defense problem where a single defender is tasked to capture a sequence of incoming intruders. The intruders' objective is to breach the target boundary without being captured by the defender. As soon as the current intruder breaches the target or gets captured by the defender, the next intruder appears at a random location on a fixed circle surrounding the target. Therefore, the defender's final location at the end of the current game becomes its initial location for the next game. Thus, the players pick strategies that are advantageous for the current as well as for the future games. Depending on the information available to the players, each game is divided into two phases: partial information and full information phase. Under some assumptions on the sensing and speed capabilities, we analyze the agents' strategies in both phases. We derive equilibrium strategies for both the players to optimize the capture percentage using the notions of engagement surface and capture circle. We quantify the percentage of capture for both finite and infinite sequences of incoming intruders.

Defending a Perimeter from a Ground Intruder Using an Aerial Defender: Theory and Practice

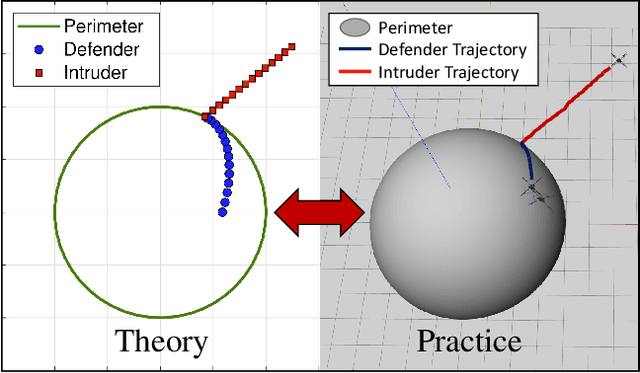
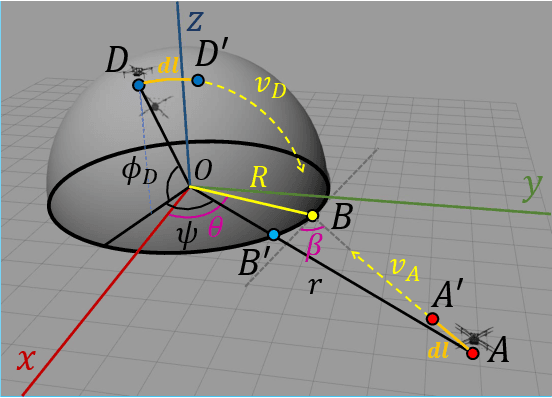
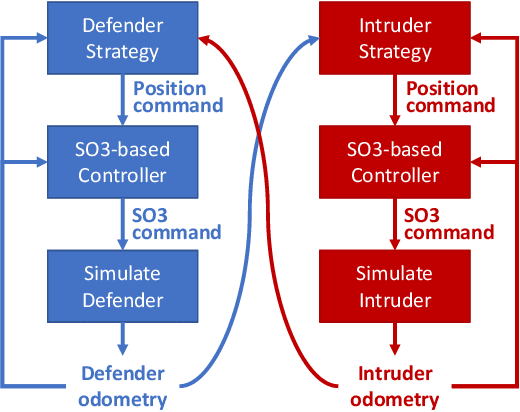
The perimeter defense game has received interest in recent years as a variant of the pursuit-evasion game. A number of previous works have solved this game to obtain the optimal strategies for defender and intruder, but the derived theory considers the players as point particles with first-order assumptions. In this work, we aim to apply the theory derived from the perimeter defense problem to robots with realistic models of actuation and sensing and observe performance discrepancy in relaxing the first-order assumptions. In particular, we focus on the hemisphere perimeter defense problem where a ground intruder tries to reach the base of a hemisphere while an aerial defender constrained to move on the hemisphere aims to capture the intruder. The transition from theory to practice is detailed, and the designed system is simulated in Gazebo. Two metrics for parametric analysis and comparative study are proposed to evaluate the performance discrepancy.

Perimeter-defense Game between Aerial Defender and Ground Intruder

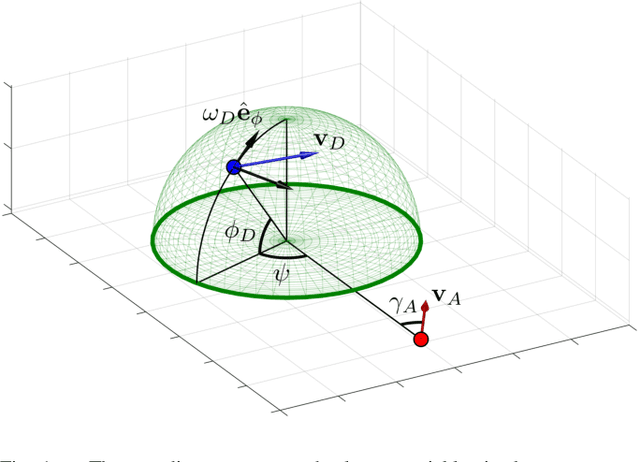
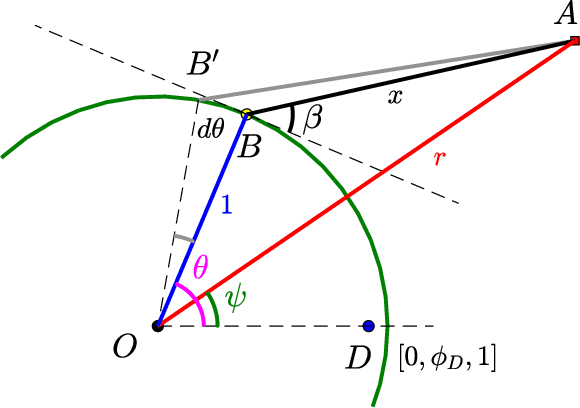
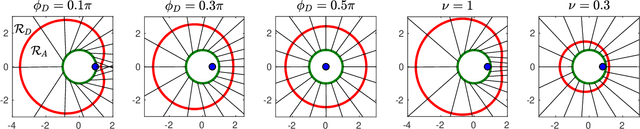
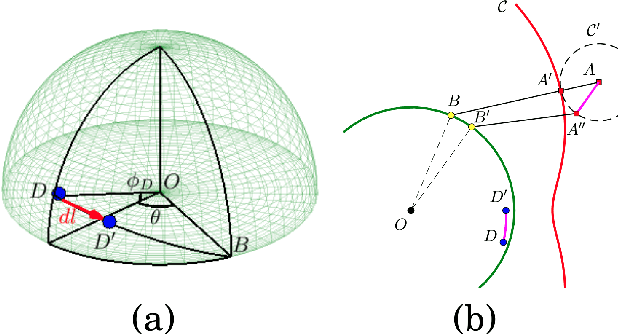
We study a variant of pursuit-evasion game in the context of perimeter defense. In this problem, the intruder aims to reach the base plane of a hemisphere without being captured by the defender, while the defender tries to capture the intruder. The perimeter-defense game was previously studied under the assumption that the defender moves on a circle. We extend the problem to the case where the defender moves on a hemisphere. To solve this problem, we analyze the strategies based on the breaching point at which the intruder tries to reach the target and predict the goal position, defined as optimal breaching point, that is achieved by the optimal strategies on both players. We provide the barrier that divides the state space into defender-winning and intruder-winning regions and prove that the optimal strategies for both players are to move towards the optimal breaching point. Simulation results are presented to demonstrate that the optimality of the game is given as a Nash equilibrium.