Heterogeneous Team Coordination on Partially Observable Graphs with Realistic Communication
Paper and Code
Oct 29, 2024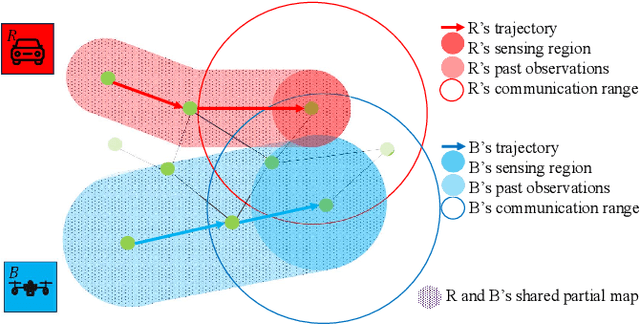

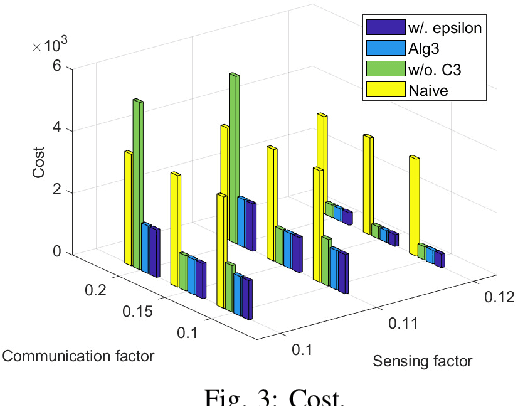
Team Coordination on Graphs with Risky Edges (\textsc{tcgre}) is a recently proposed problem, in which robots find paths to their goals while considering possible coordination to reduce overall team cost. However, \textsc{tcgre} assumes that the \emph{entire} environment is available to a \emph{homogeneous} robot team with \emph{ubiquitous} communication. In this paper, we study an extended version of \textsc{tcgre}, called \textsc{hpr-tcgre}, with three relaxations: Heterogeneous robots, Partial observability, and Realistic communication. To this end, we form a new combinatorial optimization problem on top of \textsc{tcgre}. After analysis, we divide it into two sub-problems, one for robots moving individually, another for robots in groups, depending on their communication availability. Then, we develop an algorithm that exploits real-time partial maps to solve local shortest path(s) problems, with a A*-like sub-goal(s) assignment mechanism that explores potential coordination opportunities for global interests. Extensive experiments indicate that our algorithm is able to produce team coordination behaviors in order to reduce overall cost even with our three relaxations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge