Multi-Robot Coordination Induced in Hazardous Environments through an Adversarial Graph-Traversal Game

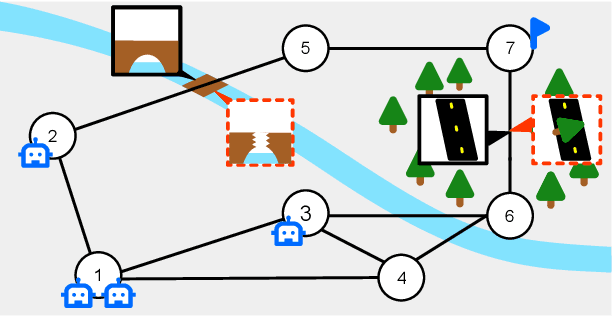
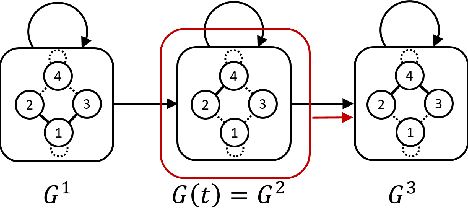
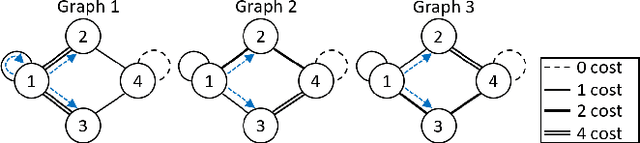
This paper presents a game theoretic formulation of a graph traversal problem, with applications to robots moving through hazardous environments in the presence of an adversary, as in military and security applications. The blue team of robots moves in an environment modeled by a time-varying graph, attempting to reach some goal with minimum cost, while the red team controls how the graph changes to maximize the cost. The problem is formulated as a stochastic game, so that Nash equilibrium strategies can be computed numerically. Bounds are provided for the game value, with a guarantee that it solves the original problem. Numerical simulations demonstrate the results and the effectiveness of this method, particularly showing the benefit of mixing actions for both players, as well as beneficial coordinated behavior, where blue robots split up and/or synchronize to traverse risky edges.