Perimeter-defense Game between Aerial Defender and Ground Intruder
Paper and Code
Dec 29, 2020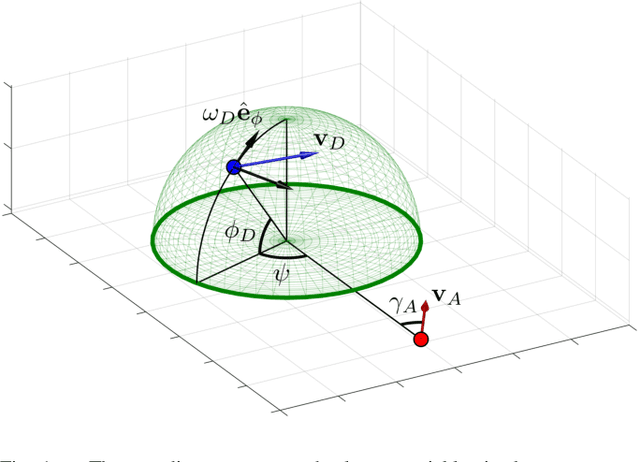
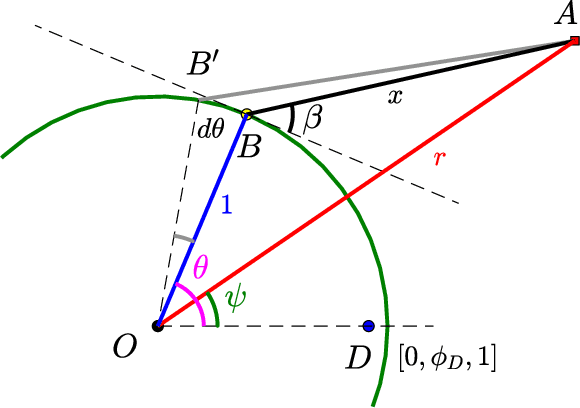
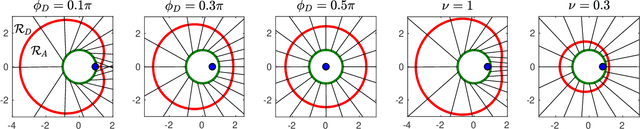
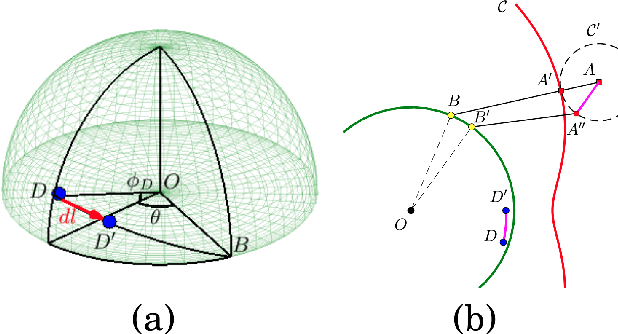
We study a variant of pursuit-evasion game in the context of perimeter defense. In this problem, the intruder aims to reach the base plane of a hemisphere without being captured by the defender, while the defender tries to capture the intruder. The perimeter-defense game was previously studied under the assumption that the defender moves on a circle. We extend the problem to the case where the defender moves on a hemisphere. To solve this problem, we analyze the strategies based on the breaching point at which the intruder tries to reach the target and predict the goal position, defined as optimal breaching point, that is achieved by the optimal strategies on both players. We provide the barrier that divides the state space into defender-winning and intruder-winning regions and prove that the optimal strategies for both players are to move towards the optimal breaching point. Simulation results are presented to demonstrate that the optimality of the game is given as a Nash equilibrium.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge